双向链表和双向循环链表
双向链表简介
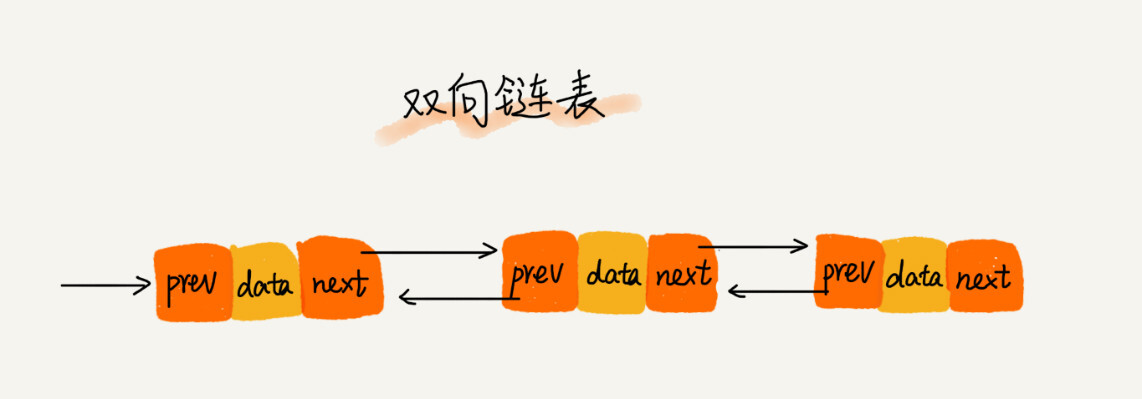
单向链表只有一个方向，结点只有一个后继指针 next 指向后面的结点。而双向链表，顾名思义，它支持两个方向，每个结点不止有一个后继指针 next 指向后面的结点，还有一个前驱指针 prev 指向前面的结点。
从上图中可以看出来，双向链表需要额外的两个空间来存储后继结点和前驱结点的地址。所以，如果存储同样多的数据，双向链表要比单链表占用更多的内存空间。虽然两个指针比较浪费存储空间，但可以支持双向遍历，这样也带来了双向链表操作的灵活性。那相比单链表，双向链表适合解决哪种问题呢？
从结构上来看，双向链表可以支持 O(1) 时间复杂度的情况下找到前驱结点，正是这样的特点，也使双向链表在某些情况下的插入、删除等操作都要比单链表简单、高效。
双向链表的增删改查操作
1. 插入操作
- 头部插入：时间复杂度O(1)
- 尾部插入：时间复杂度O(1)
- 指定位置后面插入：时间复杂度O(1)
- 指定位置前面插入：时间复杂度O(1) ---注意和单向链表的区别
2. 删除操作
删除操作的时间复杂度和插入操作的时间复杂度类似。
- 删除头部节点：时间复杂度O(1)
- 删除尾部节点：时间复杂度O(1)
- 删除值等于某个数的节点：时间复杂度O(n)
- 删除某个具体节点：O(1)
关于删除操作，这边做下说明。
在实际的软件开发中，从链表中删除一个数据无外乎这两种情况：
-
删除结点中“值等于某个给定值”的结点；
-
删除给定指针指向的结点。
对于第一种情况，不管是单链表还是双向链表，为了查找到值等于给定值的结点，都需要从头结点开始一个一个依次遍历对比，直到找到值等于给定值的结点，然后再通过我前面讲的指针操作将其删除。
尽管单纯的删除操作时间复杂度是 O(1)，但遍历查找的时间是主要的耗时点，对应的时间复杂度为 O(n)。根据时间复杂度分析中的加法法则，删除值等于给定值的结点对应的链表操作的总时间复杂度为 O(n)。
对于第二种情况，我们已经找到了要删除的结点，但是删除某个结点 q 需要知道其前驱结点，而单链表并不支持直接获取前驱结点，所以，为了找到前驱结点，我们还是要从头结点开始遍历链表，直到 p->next=q，说明 p 是 q 的前驱结点。
但是对于双向链表来说，这种情况就比较有优势了。因为双向链表中的结点已经保存了前驱结点的指针，不需要像单链表那样遍历。所以，针对第二种情况，单链表删除操作需要 O(n) 的时间复杂度，而双向链表只需要在 O(1) 的时间复杂度内就搞定了！
除了插入、删除操作有优势之外，对于一个有序链表，双向链表的按值查询的效率也要比单链表高一些。因为，我们可以记录上次查找的位置 p，每次查询时，根据要查找的值与 p 的大小关系，决定是往前还是往后查找，所以平均只需要查找一半的数据。
现在，你有没有觉得双向链表要比单链表更加高效呢？这就是为什么在实际的软件开发中，双向链表尽管比较费内存，但还是比单链表的应用更加广泛的原因。如果你熟悉 Java 语言，你肯定用过 LinkedHashMap 这个容器。如果你深入研究 LinkedHashMap 的实现原理，就会发现其中就用到了双向链表这种数据结构。
3. 更新操作
- 更新指定节点：时间复杂度O(1)
- 将链表中值等于某个具体值的节点更新：时间复杂度O(n)
4. 查询操作
- 时间复杂度：O(n)
双向链表的Java代码实现
public class TwoWayLinkedList<E> {
public static void main(String[] args) {
TwoWayLinkedList<Integer> list = new TwoWayLinkedList<>();
//尾部插入，遍历链表输出
System.out.println("尾部插入[1-10]");
for (int i = 1; i <= 10; i++) {
list.addLast(Integer.valueOf(i));
}
list.printList();
//头部插入，遍历链表输出
System.out.println("头部插入[1-10]");
for (int i = 1; i <= 10; i++) {
list.addFirst(Integer.valueOf(i));
}
list.printList();
//在指定节点后面插入
System.out.println("在头节点后面插入[100]");
list.addAfter(100, list.head);
list.printList();
System.out.println("在头节点前面插入[100]");
list.addBefore(100, list.head);
list.printList();
System.out.println("在尾节点前面插入[100]");
list.addBefore(100, list.tail);
list.printList();
System.out.println("在尾节点后面插入[100]");
list.addAfter(100, list.tail);
list.printList();
System.out.println("------------删除方法测试-----------");
System.out.println("删除头节点");
list.removeFirst();
list.printList();
System.out.println("删除尾节点");
list.removeLast();
list.printList();
System.out.println("删除指定节点");
list.removeNode(list.head.next);
list.printList();
}
private Node head;
private Node tail;
public TwoWayLinkedList() {
}
public TwoWayLinkedList(E data) {
Node node = new Node<>(data, null,null);
head = node;
tail = node;
}
public void printList() {
Node p = head;
while (p != null && p.next != null) {
System.out.print(p.data + "-->");
p = p.next;
}
if (p != null) {
System.out.println(p.data);
}
}
public void addFirst(E data) {
Node newNode = new Node(data,null ,head);
if(head!=null){
head.pre = newNode;
}
head = newNode;
if (tail == null) {
tail = newNode;
}
}
public void addLast(E data) {
Node newNode = new Node(data, tail,null);
if (tail == null) {
head = newNode;
tail = newNode;
} else {
tail.next = newNode;
tail = newNode;
}
}
/**
* @param data
* @param node node节点必须在链表中
*/
public void addAfter(E data, Node node) {
if (node == null) {
return;
}
Node newNode = new Node(data, node,node.next);
if(node.next!=null){
node.next.pre = newNode;
}
node.next = newNode;
if (tail == node) {
tail = newNode;
}
}
public void addBefore(E data, Node node) {
if (node == null) {
return;
}
if(node==head){
addFirst(data);
}else {
Node newNode = new Node(data,node.pre,node);
node.pre.next = newNode;
node.pre = newNode;
}
}
public void removeFirst() {
if (head == null) {
return;
}
if (head == tail) {
head = null;
tail = null;
} else {
if(head.next!=null){
head.next.pre = null;
}
head = head.next;
}
}
public void removeLast() {
if (tail == null) {
return;
}
if (head == tail) {
head = null;
tail = null;
} else {
if(tail.pre!=null){
tail.pre.next = null;
Node p = tail.pre;
tail.pre = null;
tail = p;
}
}
}
public void removeNode(Node node) {
if (node == null) {
return;
}
if(node==head){
removeFirst();
}
if(node==tail){
removeLast();
}
node.pre.next = node.next;
node.next.pre = node.pre;
}
private static class Node<E> {
E data;
Node pre;
Node next;
public Node(E data, Node pre, Node next) {
this.data = data;
this.pre = pre;
this.next = next;
}
}
}
双向链表的JDK实现
JDK中的LinkedList就是一个双向链表。我们可以直接拿来使用，或者做简单的封装。
package com.csx.algorithm.link;
import java.util.Collection;
import java.util.Collections;
import java.util.LinkedList;
import java.util.Set;
import java.util.function.Predicate;
public class SinglyLinkedList2<E> {
private LinkedList<E> list;
public SinglyLinkedList2() {
this.list = new LinkedList<>();
}
public SinglyLinkedList2(E data){
Set<E> singleton = Collections.singleton(data);
this.list = new LinkedList<>(singleton);
}
public SinglyLinkedList2(Collection<? extends E> c){
this.list = new LinkedList<>(c);
}
// ----------------------------------新增方法---------------------------------------
public void addFirst(E data){
list.addFirst(data);
}
public void addLast(E data){
list.addLast(data);
}
// 在链表末尾添加
public boolean add(E date){
return list.add(date);
}
public boolean addAll(Collection<? extends E> collection){
return list.addAll(collection);
}
public boolean addBefore(E data,E succ){
int i = list.indexOf(succ);
if(i<0){
return false;
}
list.add(i,data);
return true;
}
public boolean addAfter(E data,E succ){
int i = list.indexOf(succ);
if(i<0){
return false;
}
if((i+1)==list.size()){
list.addLast(data);
return true;
}else {
list.add(i+1,data);
return true;
}
}
// ---------------------------------- 删除方法---------------------------------------
// 删除方法，默认删除链表头部元素
public E remove(){
return list.remove();
}
// 删除方法,删除链表第一个元素
public E removeFirst(){
return list.removeFirst();
}
// 删除方法,删除链表最后一个元素
public E removeLast(){
return list.removeLast();
}
// 删除链表中第一次出现的元素，成功删除返回true
// 对象相等的标准是调用equals方法相等
public boolean remove(E data){
return list.remove(data);
}
// 逻辑和remove（E data）方法相同
public boolean removeFirstOccur(E data){
return list.removeFirstOccurrence(data);
}
// 因为LinkedList内部是双向链表，所以时间复杂度和removeFirstOccur相同
public boolean removeLastOccur(E data){
return list.removeLastOccurrence(data);
}
// 批量删除方法
public boolean removeAll(Collection<?> collection){
return list.removeAll(collection);
}
// 按照条件删除
public boolean re(Predicate<? super E> filter){
return list.removeIf(filter);
}
// ----------------------------- 查询方法----------------------------
// 查询链表头部元素
public E getFirst(){
return list.getFirst();
}
// 查询链表尾部元素
public E getLast(){
return list.getLast();
}
// 查询链表是否包含某个元素
// 支持null判断
// 相等的标准是data.equals(item)
public boolean contains(E data){
return list.contains(data);
}
public boolean containsAll(Collection<?> var){
return list.containsAll(var);
}
}
还是做下提醒，LinkedList并不是线程安全的。如果需要保证线程安全，需要你自己做同步控制。
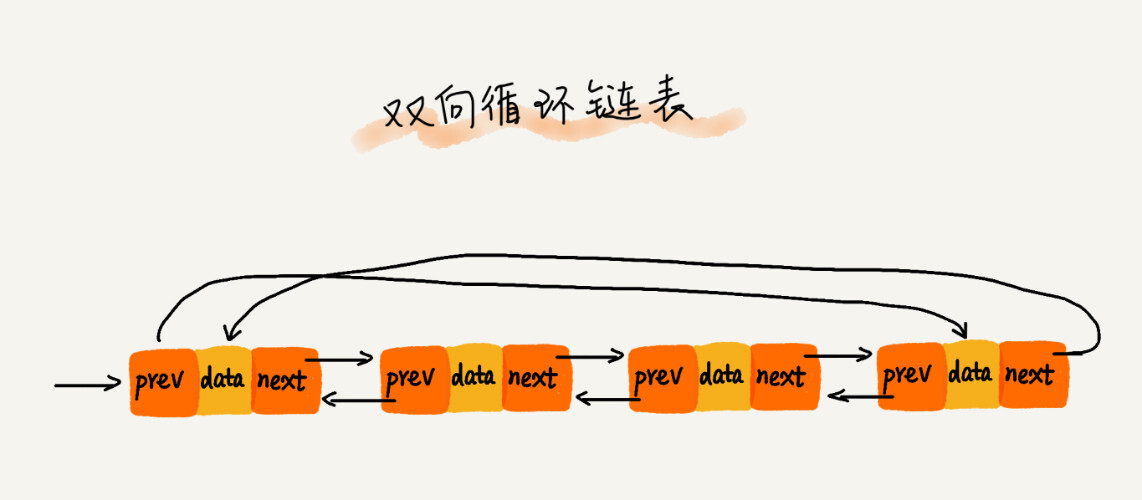
双向循环链表
其实就是将头节点的前趋指针指向尾节点，将尾节点的后驱指针指向头节点。
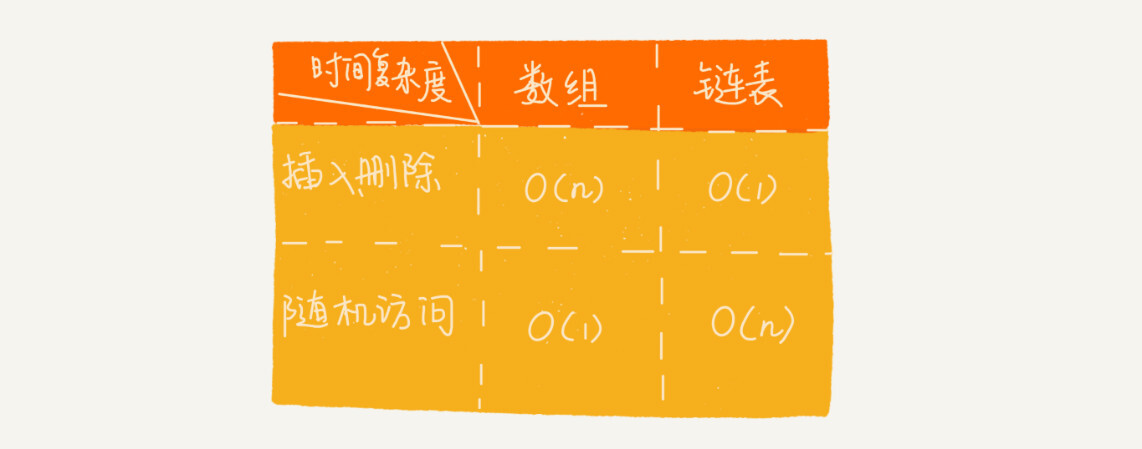
数组和链表的比较
不过，数组和链表的对比，并不能局限于时间复杂度。而且，在实际的软件开发中，不能仅仅利用复杂度分析就决定使用哪个数据结构来存储数据。
数组简单易用，在实现上使用的是连续的内存空间，可以借助 CPU 的缓存机制，预读数组中的数据，所以访问效率更高。而链表在内存中并不是连续存储，所以对 CPU 缓存不友好，没办法有效预读。
数组的缺点是大小固定，一经声明就要占用整块连续内存空间。如果声明的数组过大，系统可能没有足够的连续内存空间分配给它，导致“内存不足（out of memory）”。如果声明的数组过小，则可能出现不够用的情况。这时只能再申请一个更大的内存空间，把原数组拷贝进去，非常费时。链表本身没有大小的限制，天然地支持动态扩容，我觉得这也是它与数组最大的区别。
除此之外，如果你的代码对内存的使用非常苛刻，那数组就更适合你。因为链表中的每个结点都需要消耗额外的存储空间去存储一份指向下一个结点的指针，所以内存消耗会翻倍。而且，对链表进行频繁的插入、删除操作，还会导致频繁的内存申请和释放，容易造成内存碎片，如果是 Java 语言，就有可能会导致频繁的 GC（Garbage Collection，垃圾回收）。所以，在我们实际的开发中，针对不同类型的项目，要根据具体情况，权衡究竟是选择数组还是链表。
