线性表结构：数组

什么是数组

数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。对于数组，你要掌握两个关键点。

1. 线性表

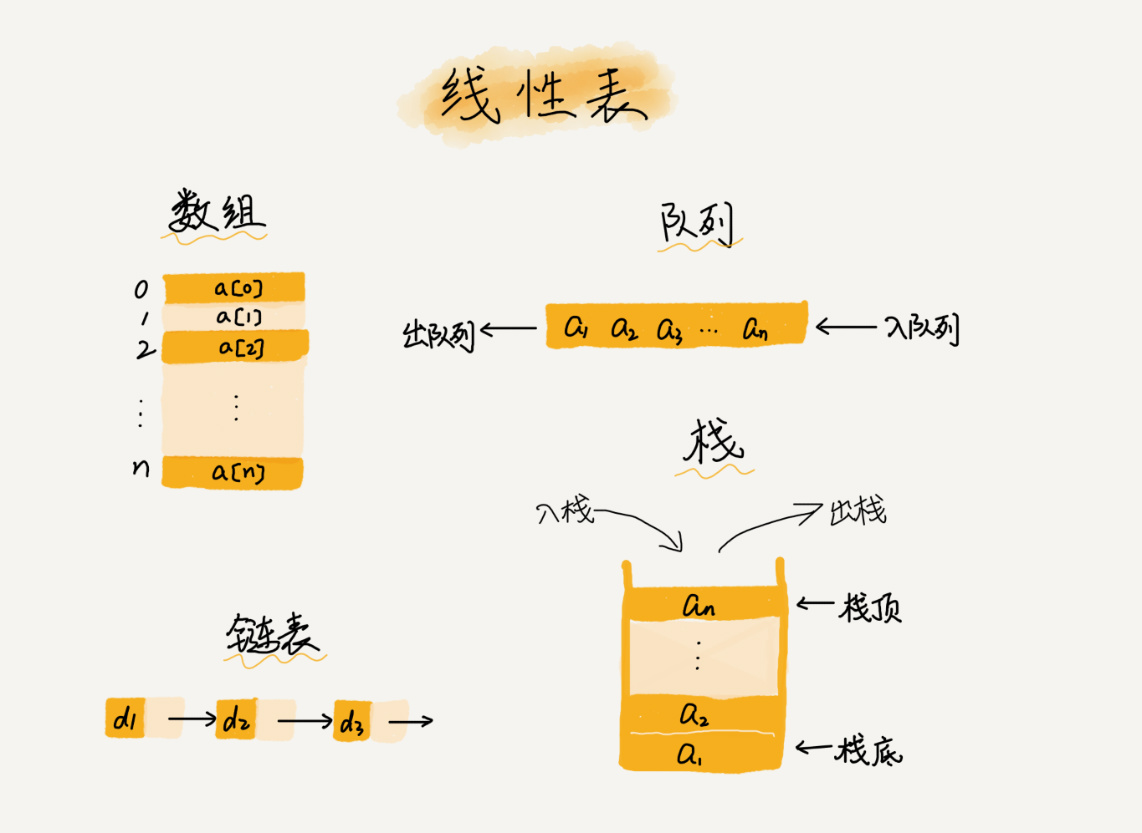
线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组，链表、队列、栈等也是线性表结构。

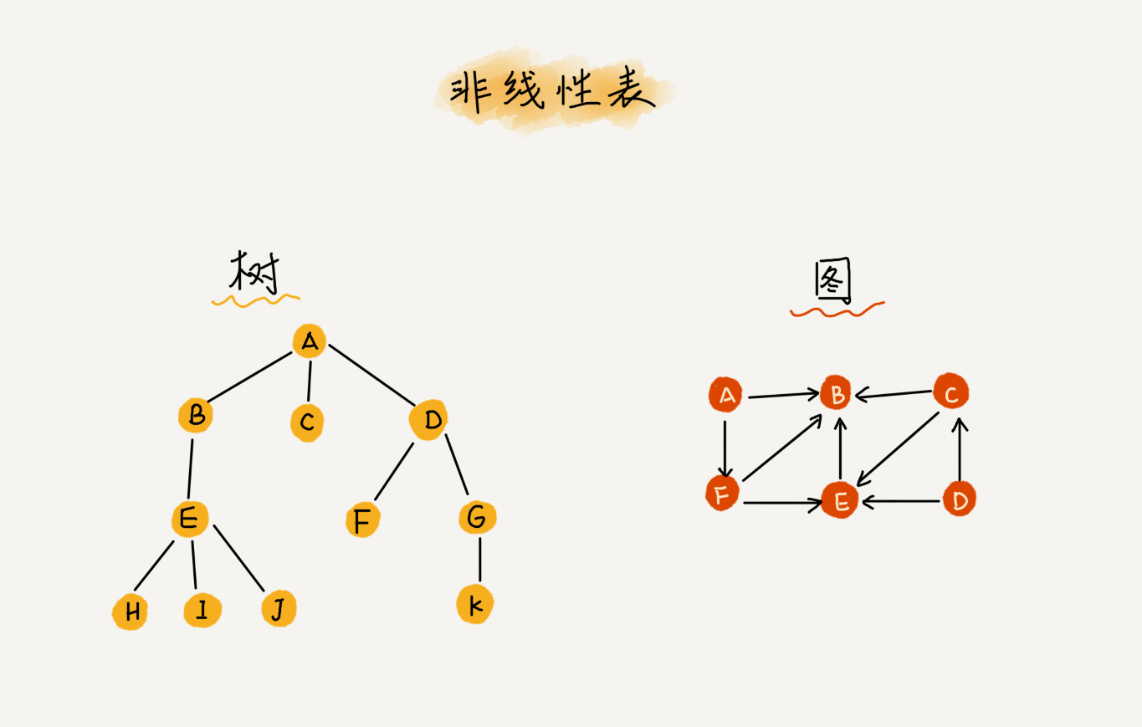
而与它相对立的概念是非线性表，比如二叉树、堆、图等。之所以叫非线性，是因为，在非线性表中，数据之间并不是简单的前后关系。比如说下面树形结构中的D节点就有三个方向的数据。

2. 连续的内存空间和相同类型的数据

数组的存储空间是连续的，而且必须存储相同类型的数据。正是因为这两个限制，它才有了一个堪称“杀手锏”的特性：“随机访问”。但有利就有弊，这两个限制也让数组的很多操作变得非常低效，比如要想在数组中删除、插入一个数据，为了保证连续性，就需要做大量的数据搬移工作。

这边解释下随机访问的含义。随机访问是指通过元素的下标能立马定位到元素在数组中的位置，随机查找的时间复杂度为O(1)。
有的人可能把在数组中查找元素和随机访问搞混了。在数组中查找元素必须进行数组遍历，时间复杂度是O(n)，即使是排序的数组，通过二分查找，时间复杂度是O(logn)。

低效的“插入”和“删除”

1. 插入操作

假设数组的长度为 n，现在，如果我们需要将一个数据插入到数组中的第 k 个位置。为了把第 k 个位置腾出来，给新来的数据，我们需要将第 k～n 这部分的元素都顺序地往后挪一位。这个操作的时间复杂度是O(n)。

如果数组中的数据是有序的，我们在某个位置插入一个新的元素时，就必须按照刚才的方法搬移 k 之后的数据。但是，如果数组中存储的数据并没有任何规律，数组只是被当作一个存储数据的集合。在这种情况下，如果要将某个数据插入到第 k 个位置，为了避免大规模的数据搬移，我们还有一个简单的办法就是，直接将第 k 位的数据搬移到数组元素的最后，把新的元素直接放入第 k 个位置。

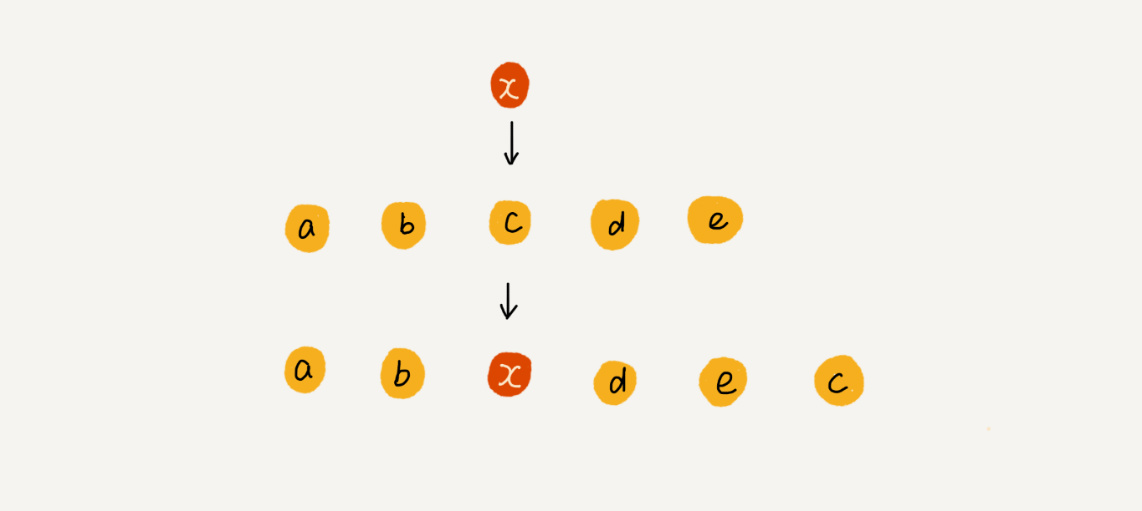
为了更好地理解，我们举一个例子。假设数组 a[10]中存储了如下 5 个元素：a，b，c，d，e。我们现在需要将元素 x 插入到第 3 个位置。我们只需要将 c 放入到 a[5]，将 a[2]赋值为 x 即可。最后，数组中的元素如下： a，b，x，d，e，c。

利用这种处理技巧，在特定场景下，在第 k 个位置插入一个元素的时间复杂度就会降为 O(1)。（直接将指定位置的元素放到数组最后一位后面array[array.length]=k）

2. 删除操作
跟插入数据类似，如果我们要删除第 k 个位置的数据，为了内存的连续性，也需要搬移数据，不然中间就会出现空洞，内存就不连续了。删除操作的时间复杂度也是O(n)。

实际上，在某些特殊场景下，我们并不一定非得追求数组中数据的连续性。如果我们将多次删除操作集中在一起执行，删除的效率是不是会提高很多呢？

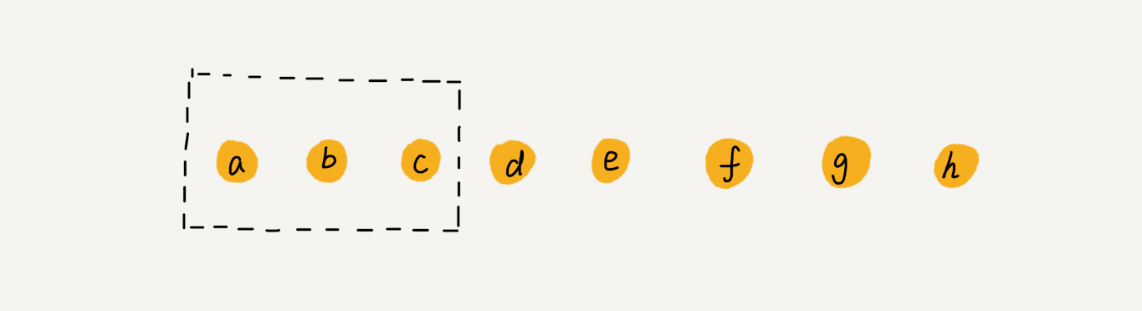
我们继续来看例子。数组 a[10]中存储了 8 个元素：a，b，c，d，e，f，g，h。现在，我们要依次删除 a，b，c 三个元素。

为了避免 d，e，f，g，h 这几个数据会被搬移三次，我们可以先记录下已经删除的数据。每次的删除操作并不是真正地搬移数据，只是记录数据已经被删除。当数组没有更多空间存储数据时，我们再触发执行一次真正的删除操作，这样就大大减少了删除操作导致的数据搬移。

如果你了解 JVM，你会发现，这不就是 JVM 标记清除垃圾回收算法的核心思想。

关于数组使用的几个注意点

• 小心数组越界访问（一般在数组的长度范围内访问数组元素是没什么问题的）；
• 小心数组元素为空，数组某个下标位置上的值可能是空的，如果不做判断的话可能会发生空指针异常。

怎么实现数组这种数据结构

数组是每个编程语言都会直接提供的数据结构。而且很多语言提供了更高级的容器实现，比如Java中的ArrayList。ArrayList 最大的优势就是可以将很多数组操作的细节封装起来。比如前面提到的数组插入、删除数据时需要搬移其他数据等。另外，它还有一个优势，就是支持动态扩容。

数组本身在定义的时候需要预先指定大小，因为需要分配连续的内存空间。如果我们申请了大小为 10 的数组，当第 11 个数据需要存储到数组中时，我们就需要重新分配一块更大的空间，将原来的数据复制过去，然后再将新的数据插入。

如果使用 ArrayList，我们就完全不需要关心底层的扩容逻辑，ArrayList 已经帮我们实现好了。每次存储空间不够的时候，它都会将空间自动扩容为 1.5 倍大小。

不过，这里需要注意一点，因为扩容操作涉及内存申请和数据搬移，是比较耗时的。所以，如果事先能确定需要存储的数据大小，最好在创建 ArrayList 的时候事先指定数据大小。

作为高级语言编程者，是不是数组就无用武之地了呢？当然不是，有些时候，用数组会更合适些，我总结了几点自己的经验：

• Java ArrayList 无法存储基本类型，比如 int、long，需要封装为 Integer、Long 类，而 Autoboxing、Unboxing 则有一定的性能消耗，所以如果特别关注性能，或者希望使用基本类型，就可以选用数组。
• 如果数据大小事先已知，并且对数据的操作非常简单，用不到 ArrayList 提供的大部分方法，也可以直接使用数组；
• 还有一个是我个人的喜好，当要表示多维数组时，用数组往往会更加直观。比如 Object[][] array；而用容器的话则需要这样定义：ArrayList > array；

对于业务开发，直接使用容器就足够了，省时省力。毕竟损耗一丢丢性能，完全不会影响到系统整体的性能。但如果你是做一些非常底层的开发，比如开发网络框架，性能的优化需要做到极致，这个时候数组就会优于容器，成为首选。

有趣的知识点

数组的下标为什么从0开始？

其实数组的下标更确切的表述是相对于首地址的偏移量，这样更容易寻址。

从数组存储的内存模型上来看，“下标”最确切的定义应该是“偏移（offset）”。前面也讲到，如果用 a 来表示数组的首地址，a[0]就是偏移为 0 的位置，也就是首地址，a[k]就表示偏移 k 个 type_size 的位置，所以计算 a[k]的内存地址只需要用这个公式： a[k]_address = base_address + k * type_size 但是，如果数组从 1 开始计数，那我们计算数组元素 a[k]的内存地址就会变为： a[k]_address = base_address + (k-1)*type_size

一些网友留言

1. 数组的一些其他应用

数组的应用真的很多，比如redis的内部实现，压缩链表，快速链表，还有后来搞出一个紧凑列表来替代压缩列表。而且很多自定义协议都是用数组做的，比如rocketmq的协议，前面几位代表什么，后面几位代表什么。

2. 标记清除法

标记清除具体步骤如下：

• 开始标记并程序暂停（stop the world）；
• 找到所有可达对象，并做上标记;
• 标记完成后开始清除未标记的对象;
• 清除完成;

其实所有的垃圾收集算法都可以分为：标记阶段和收集阶段。只是不同的垃圾回收机制在这两个阶段使用的算法不一样。

标记清除法带来的问题

• STW (stop the world) 标记对象的时候程序需要暂停，导致程序出现卡顿，如果经常进行STW操作，程序性能将大幅下降；
• 标记需要扫描整个堆；
• 清除对象会产生堆碎片。

STW指的是JVM把所有线程都暂停了，这样所有的对象都不会被修改，这个时候去扫描是绝对安全的。

3. 画图软件推荐

ipad Paper

4.分代收集法
分代收集算法（针对JDK1.8以下）：
根据对象的存活周期分为老年代，新生代，永久代
a、在新生代中，每次GC时都发现有大批对象死去，只有少量存活，使用复制算法。即在垃圾回收时，将正在使用的内存中存活对象复制到另一块未使用的内存中。之后清理正在使用的内存中所有对象，交换两块内存角色。反复进行，完成垃圾回收。
b、在老年代中，因为对象存活率高、没有额外空间对他进行分配担保，使用“标记-清理”/“标记-整理”算法。即在标记阶段，遍历所有的GC Roots，然后将所有GC Roots可达的对象标记为存活的对象。清除阶段，清除的过程将遍历堆中所有的对象，将没有标记的对象全部清除掉。
c、永久代（Permanet Generation）/ 元空间（Metaspace）
永久代用于存储已被虚拟机加载的类信息、常量、静态变量、即时编译后的代码等数据。是JVM规范中方法区的具体实现。
是Hotspot虚拟机特有的概念，方法区/永久代是非堆内存。