数据结构：二叉查找树（BST）

1. 什么是BST#

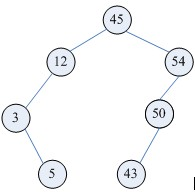
对于二叉树中的每个节点X，它的左子树中所有项的值都小于X中的项，它的右子树中所有项的值大于X中的项。这样的二叉树是二叉查找树。

以上是一颗二叉查找树，其特点是：

（1）若它的左子树不为空，则左子树上的所有节点的值都小于它的根节点的值；
（2）若它的右子树不为空，则右子树上所有节点的值都大于它的根节点的值；
（3）其他的左右子树也分别为二叉查找树；
（4）二叉查找树是动态查找表，在查找的过程中可见添加和删除相应的元素，在这些操作中需要保持二叉查找树的以上性质。

2. 二叉查找树的定义#

根据二叉查找树的要求，我们首先让BinaryNode实现Comparable接口。

// 树节点
class BinaryNode implements Comparable {

    Integer element;

    BinaryNode left;

    BinaryNode right;

    public BinaryNode{

    }

    public BinaryNode(Integer element, BinaryNode left, BinaryNode right) {
        this.element = element;
        this.left = left;
        this.right = right;
    }

    @Override
    public int compareTo(@NonNull Object o) {
        return this.element - (Integer) o;
    }
}

下面我们完成对BinarySearchTree的定义（只定义关键轮廓，具体接口后续进行分析）。

public class BinarySearchTree {

    //定义树的根节点
    BinaryNode root;

    public BinarySearchTree() {
        this.root = null;
    }

    public void makeEmpty() {
        this.root = null;
    }

    public boolean isEmpty() {
        return this.root == null;
    }

    // 判断是否包含某个元素
    public boolean contains(Integer x) {
        //TODO:后续讲解
        return false;
    }

    // 查找最小值
    public BinaryNode findMin(){
        //TODO:后续讲解
        return null;
    }

    // 查找最大值
    public BinaryNode findMax(){
        //TODO:后续讲解
        return null;
    }

    // 按照顺序插入值
    public void insert(Integer x){
        //TODO:后续讲解
    }

    // 删除某个值
    public void remove(Integer x){
        //TODO:后续讲解
    }
    
    // 打印树
    public void printTree(){
        //TODO:后续讲解
    }
}

3. contaions操作#

如果在树T中包含项X的节点，那么该操作返回true，否则返回false。

树的结构使得这种操作变得非常简单，如果T为空集，直接返回false；否则我们就对T的左子树或右子树进行递归查找，直到找到该项X。

代码实现如下：

/**
     * 是否包含某个元素
     * @param x 待查找对象
     * @return 查找结果
     */
    public boolean contains(Integer x) {
        // 首次查找从根节点开始
        return contains(x,root);
    }

    private boolean contains(Integer x, BinaryNode node) {
        // 根节点为空的情况，不需要再查找
        if (node == null) {
            return false;
        }
        
        // 与当前节点进行比较
        int compareResult = x.compareTo(node.element);

        // 小于当前节点的值，就递归遍历左子树
        if (compareResult < 0) {
            return contains(x, node.left);
        } 
        // 大于当前节点的值，就递归遍历右子树
        else if (compareResult > 0) {
            return contains(x, node.right);
        } 
        // 等于当前节点值，直接返回
        else {
            return true;
        }
    }

4. 查找最小节点#

从根开始并且只要有左子树就向左进行，终止点就是最小元素节点。

// 查找最小值
    public BinaryNode findMin() {
        return findMin(root);
    }

    private BinaryNode findMin(BinaryNode node) {
        // 当前节点为null，直接返回null
        if (node == null) {
            return null;
        }

        // 不存在左子树，返回当前节点
        if (node.left == null) {
            return node;
        }

        // 递归遍历左子树
        return findMin(node.left);

    }

5. 查找最大节点#

从根开始并且只要有右子树就向右进行，终止点就是最大元素节点。作为与findMin的对比，findMax方法我们抛弃了常用的递归，使用了常见的while循环来查找。

 // 查找最大值
    public BinaryNode findMax() {
        return findMax(root);
    }

    private BinaryNode findMax(BinaryNode node) {
        if (node != null) {
            while (node.right != null) {
                node = node.right;
            }
        }
        return node;
    }

6. insert操作#

插入操作在概念上是简单的，为了将X插入树T中，我们像contains一样沿着树查找。
如果找到X，那么我们可以什么都不做，也可以做一些更新操作。
否则，就将X插入到遍历路径上的最后一个节点。(这个做法有待商榷)

代码实现如下：

public void insert(Integer x) {
        root = insert(x, root);
    }

    // 返回的插入节点的根节点
    private BinaryNode insert(Integer x, BinaryNode node) {
        // 如果当前节点为null，新建节点返回
        if (node == null) {
            return new BinaryNode(x, null, null);
        }
        // 与当前节点比较
        int compareResult = x.compareTo(node.element);

        // 小于当前节点值，递归插入左子树，并将返回值设置为当前节点的left
        if (compareResult < 0) {
            node.left = insert(x, node.left);
        }


         // 大于当前节点值，递归插入右子树，并将返回值设置为当前节点的right
        if (compareResult > 0) {
            node.right = insert(x, node.right);
        }

        // 等于当前的值，不做任何处理
        if (compareResult == 0) {
            // do some update or do noting
        }
        
        return node;

    }

7. 删除操作#

正如许多数据结构一样，最难的操作是remove,一旦我们发现了要删除的元素，就要考虑几种可能的情况：

当待删除的节点为叶子节点时，直接删除。
当待删除节点只有一个儿子节点时，把儿子节点代替该节点的位置，然后删除该节点。
当待删除的节点有两个儿子节点时，一般的删除策略是用其右子树的最小的数据代替该节点的数据并递归删除那个节点(现在它是空的);因为右子树的最小节点不可能有左儿子，所以第二次Delete要容易。

    // 删除某个值
    public void remove(Integer x) {
        remove(x, root);
    }

    private BinaryNode remove(Integer x, BinaryNode node) {
        if (node == null) {
            return null;
        }

        int compareResult = x.compareTo(node.element);

        if (compareResult < 0) {
            node.left = remove(x, node.left);
        }

        if (compareResult > 0) {
            node.right = remove(x, node.right);
        }

        if (compareResult == 0) {

            if (node.left != null && node.right != null) {

                node.element = findMin(node.right).element;

                node.right = remove(node.element, node.right);

            } else {

                node = (node.left != null) ? node.left : node.right;

            }

        }


        return node;

    }

8. 二叉查找树的局限#

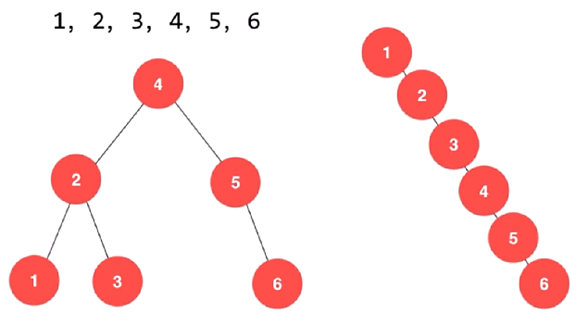
同样的数据，可以对应不同的二叉搜索树，如下：

二叉搜索树可能退化成链表，相应的，二叉搜索树的查找操作是和这棵树的高度相关的，而此时这颗树的高度就是这颗树的节点数n，同时二叉搜索树相应的算法全部退化成 O(n) 级别。

显然，说二叉搜索树的查找、插入、删除这三个操作都是O(lgn) 级别的，只是一个大概的估算，具体要和二叉搜索树的形状相关。但总的来说时间复杂度在o（logn）
到o（n）之间。

9. 简单总结#

二叉搜索树的节点查询、构造和删除性能，与树的高度相关，如果二叉搜索树能够更“平衡”一些，避免了树结构向线性结构的倾斜，则能够显著降低时间复杂度。二叉搜索树的存储方面，相对于线性结构只需要保存元素值，树中节点需要额外的空间保存节点之间的父子关系，所以在存储消耗上要高于线性结构。