LIS 最长递增子序列
2014-04-22 00:12 Loull 阅读(362) 评论(0) 编辑 收藏 举报一、最长公共子序列
经典的动态规划问题,大概的陈述如下:
给定两个序列a1,a2,a3,a4,a5,a6......和b1,b2,b3,b4,b5,b6.......,要求这样的序列使得c同时是这两个序列中的部分(不要求连续),这个就叫做公共子序列,然后最长公共子序列自然就是所有的子序列中最长的啦。

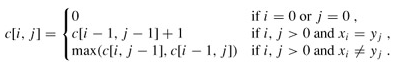
public static int lcs(String s1, String s2) { int[][] dp = new int[s1.length()+1][s2.length()+1]; for (int i=1; i<=s1.length(); i++) { for (int j=1; j<=s2.length(); j++) { if (s1.charAt(i-1) == s2.charAt(j-1)) dp[i][j] = dp[i-1][j-1] + 1; else dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]); } } return dp[s1.length()][s2.length()]; }
二、最长递增子序列
最长递增子序列,Longest Increasing Subsequence 下面我们简记为 LIS。
方法一、排序+LCS
转化成LCS问题求解,只要将这个序列排序之后与原来的序列求LCS得到的就是LIS了。
方法二、DP
像LCS一样,从后向前分析,很容易想到,第i个元素之前的最长递增子序列的长度要么是1(单独成一个序列),要么就是第i-1个元素之前的最长递增子序列加1,可以有状态方程:
LIS[i] = max{1,LIS[k]+1},其中,对于任意的k<=i-1,arr[i] > arr[k],这样arr[i]才能在arr[k]的基础上构成一个新的递增子序列。
方法三、
假设存在一个序列d[1..9] = 2 1 5 3 6 4 8 9 7,可以看出来它的LIS长度为5。
下面一步一步试着找出它。
我们定义一个序列B,然后令 i = 1 to 9 逐个考察这个序列。
此外,我们用一个变量Len来记录现在最长算到多少了
首先,把d[1]有序地放到B里,令B[1] = 2,就是说当只有1一个数字2的时候,长度为1的LIS的最小末尾是2。这时Len=1
然后,把d[2]有序地放到B里,令B[1] = 1,就是说长度为1的LIS的最小末尾是1,d[1]=2已经没用了,很容易理解吧。这时Len=1
接着,d[3] = 5,d[3]>B[1],所以令B[1+1]=B[2]=d[3]=5,就是说长度为2的LIS的最小末尾是5,很容易理解吧。这时候B[1..2] = 1, 5,Len=2
再来,d[4] = 3,它正好加在1,5之间,放在1的位置显然不合适,因为1小于3,长度为1的LIS最小末尾应该是1,这样很容易推知,长度为2的LIS最小末尾是3,于是可以把5淘汰掉,这时候B[1..2] = 1, 3,Len = 2
继续,d[5] = 6,它在3后面,因为B[2] = 3, 而6在3后面,于是很容易可以推知B[3] = 6, 这时B[1..3] = 1, 3, 6,还是很容易理解吧? Len = 3 了噢。
第6个, d[6] = 4,你看它在3和6之间,于是我们就可以把6替换掉,得到B[3] = 4。B[1..3] = 1, 3, 4, Len继续等于3
第7个, d[7] = 8,它很大,比4大,嗯。于是B[4] = 8。Len变成4了
第8个, d[8] = 9,得到B[5] = 9,嗯。Len继续增大,到5了。
最后一个, d[9] = 7,它在B[3] = 4和B[4] = 8之间,所以我们知道,最新的B[4] =7,B[1..5] = 1, 3, 4, 7, 9,Len = 5。
于是我们知道了LIS的长度为5。
!!!!! 注意。这个1,3,4,7,9不是LIS,它只是存储的对应长度LIS的最小末尾。有了这个末尾,我们就可以一个一个地插入数据。虽然最后一个d[9] = 7更新进去对于这组数据没有什么意义,但是如果后面再出现两个数字 8 和 9,那么就可以把8更新到d[5], 9更新到d[6],得出LIS的长度为6。
然后应该发现一件事情了:在B中插入数据是有序的,而且是进行替换而不需要挪动——也就是说,我们可以使用二分查找,将每一个数字的插入时间优化到O(logN)~~~~~于是算法的时间复杂度就降低到了O(NlogN)~!
package dp; import java.util.Arrays; public class LIS { public static int lis_lcs(int[] A) { int[] B = Arrays.copyOf(A, A.length); Arrays.sort(B); int[][] dp = new int[A.length+1][A.length+1]; for (int i=1; i<=A.length; i++) { for (int j=1; j<=B.length; j++) { if (A[i-1] == B[j-1]) dp[i][j] = dp[i-1][j-1] +1; else dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]); } } return dp[A.length][B.length]; } public static int lis_dp(int[] A) { int[] dp = new int[A.length]; Arrays.fill(dp, 1); int lis = 0; for (int i=0; i<A.length; i++) { for (int j=0; j<i; j++) { if (A[i] > A[j] && dp[i]<dp[j]+1) { dp[i] = dp[j] + 1; } if (lis < dp[i]) lis = dp[i]; } } return lis; } public static int lis(int[] A) { if (A.length == 0) return 0; int[] B = new int[A.length]; B[0] = A[0]; int len = 1; for (int i=1; i<A.length; i++) { int left=0, right=len; while(left <= right) { int mid = (left + right) / 2; if (B[mid] < A[i]) left = mid + 1; else right = mid -1; } B[left] = A[i]; if (left > len) len++; } return len; } public static void main(String[] args) { int[] a = {2, 1, 5, 3, 6, 4, 8, 9, 7}; System.out.println(lis_lcs(a)); System.out.println(lis_dp(a)); System.out.println(lis(a)); } }
Felix’s Blog:最长递增子序列 O(NlogN)算法


