上一篇文章（中篇）里 面，我用的示意图是因子图，而里面也出现了Psi函数，本来应该当时就解释清楚的，但实在没有精力写那么多东西，所以就想放到下篇讲的。后来发现，讲条件 随机场要结合有向无向图和independence graph，来推导模型，必须又花一些篇幅讲一下，这些都是基础背景，所以就一起推到这里来讲了。起名字还让我头疼，下已经被条件随机场预订了，这篇反正 都是背景知识，所以就叫番外篇吧。建议看整个系列的时候先看这篇，理解中和下(预计一周后动笔)就好理解多了。

其实感觉我不大适合写很长的东西，目前所有的内容，我本来准备集中一篇文章搞定的，后来想分上下部，写到中途又决定分上中下，再到现在的番外……到目前为止，我觉得写个人博客的人里面，Pongba是最擅长写篇幅很长的经典文章的，好像这小子自从去macrohard之后，就没出过什么大手笔了。我是只要内容一多，写起来自己的觉得烦了，所以每次都拿一部分推到后面写。

好了废话不多说，开始吧。

 

关于factor graph

所谓factor graph(因子图)，就是对函数因子分解的表示图，一般内含两种节点，变量节点和函数节点。我们知道，一个全局函数能够分解为多个局部函数的积，因式分 解就行了，这些局部函数和对应的变量就能体现在因子图上。比如，我现在有一个全局函数，其因子分解方程是

那么我们将其写成方便表示的

其对应的factor graph如下：

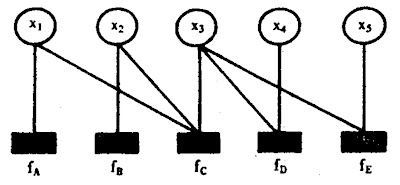
在因子图中，所有顶点，要不然就是变量节点不然就是函数节点，边线表示他们之间的函数关系。在讲解朴素贝叶斯和马尔可夫的时候，我们变线上标注的符 号，也就是Psi函数表示符号，就是表示我们模型中x和y的联系函数。Psi函数在不同的环境下有着不同的含义，因此解释这种东西总是比较棘手的。在动态 模型里面，或者任何其他的图概率模型，都是可以用因子图表示的，而Psi在这里，表征的通常都是概率或者条件概率。 因子图和Psi函数表示法，在machine learning的paper中是比较常用的。

在动态模型及其求解介绍—下一文中，有对势函数更加清楚的讲述。

关于directed/undirected/independence graph

有人看到这个标题，可能会想，靠，有向图无向图，这不是基本的图论知识么，怎么拿过来忽悠了？别急，事实上动态模型的两大类，generative和discriminative model，分别可以用有向图和无向图表示。

还记得讲马尔可夫模型的时候，用的示意图么？

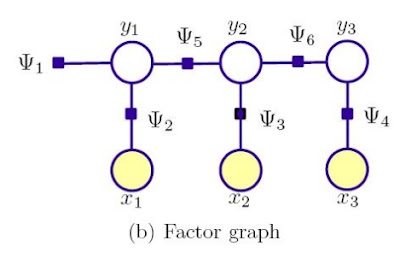
对，这就是隐马尔可夫模型的因子图。如果我们把因子图换一个形式，用independence graph来表示呢？且慢，先说说什么是independence graph，恩，在这里更准备的说法是conditional independece graph。假设我们有一个图G=(V,E)，我们让里面的每一个(x,y)组合都和其他所有的变量都条件独立，就称这是图G的independence graph表示。图G的independence graph表示中的顶点，就是图G的最大独立集合。

那么对于隐马尔可夫的因子图，它的independence graph是这样的

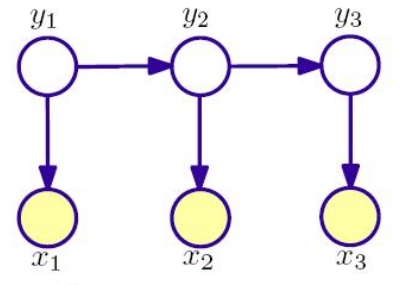
你看，这是不是一个有向图的表达形式？

好，我们再看看discriminative model的代表之一，最大熵模型的因子图

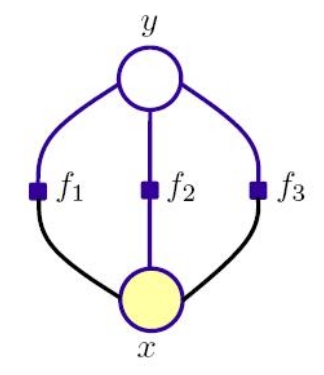
那么它的independece graph表示形式是什么呢？

看到这里，肯定有人会疑惑了。为啥两者的independece graph表示形式如此不同呢？

我们先看看隐马和朴素贝叶斯，它们都是generative模型，都针对联合概率密度建模。要知道，X和Y是贯穿整个观察和标注序列的随机变量，你 要针对他们来求联合概率密度，就不得不考虑对所有变量进行枚举，这在一个长序列中几乎是不现实的，所以才会有假设输出独立的情况。但即使你假设了输出独 立，建立起来的模型还是一个链式模型，存在多个由和组成的状态链接而成，这些状态之间就是一个传导的有向关系。

而以最大熵和CRF为代表的discriminative模型则完全不同，因为他们使用的是定义条件概率p(Y|x)的模型，关注的是，在给定一个 特定的观察序列下，label序列的条件概率，这就避免了联合分布中还要考虑观察序列的概率问题。请注意，这里是指给定的观察序列，而不是观察变量，这是 本质的区别。discriminative model中没有一种链式关系，最大熵考虑的是当前状态的最优化问题，条件随机场考虑的是全局状态的最优化问题。

如果说到这里，还是有点看不透的话，没关系，在动态模型及其求解介绍–下一文中，我会讲解条件随机场的independence graph，那时候就会理解更加深入一些了。这里只需要对这些名词有一个大致的理解即可。

××××××××××××××××××××××××××××××

系列链接：

动态模型及其求解介绍—番外篇

动态模型及其求解介绍—上

动态模型及其求解介绍—中

动态模型及其求解介绍—下