【转】动态模型及其求解介绍—下
2013-06-05 11:08 Loull 阅读(505) 评论(0) 编辑 收藏 举报之前,我们大致介绍了解线性动态模型的前三种代表性方法,并画了这么一张图来表示他们之间的关系。这一篇文章中,会对最后一种方法,CRF进行一些介绍。建议看这一篇文章之前,至少先把最大熵模型复习一遍,方便理解两者的关系。然后看看动态模型及其求解介绍—番外篇,对示意图的表示有一个比较清晰的认识。
从关系图中我们看到,和NB与HMM之间的关系一样,CRF实际上就是序列版本的ME模型。当然你可以说最大熵马尔可夫也是一个序列模型,但是中篇 文章已经提到了该模型的缺点了。而CRF则是用另一种思路去考虑问题的。也可以这样说,CRF是马尔可夫网络的一种变体。现在就来介绍一下,什么叫条件随 机场。我们从之前的模型介绍看到,动态模型都可以用图来表示,而从动态模型及其求解介绍—番外篇一 文中,我们知道了无向图表示discriminative model的方法。假设这里我们有一个图G=(V,E),用无向图表示,图中存在节点v,对应Y(标注序列)中的每一个变量Yv。如果对于每一个选出来的 随机变量Yv,都服从马尔可夫性质,我们就说(X,Y)序列集合组成一个条件随机场。画图解释一下,假设哟我们有一个图G,表示如下:
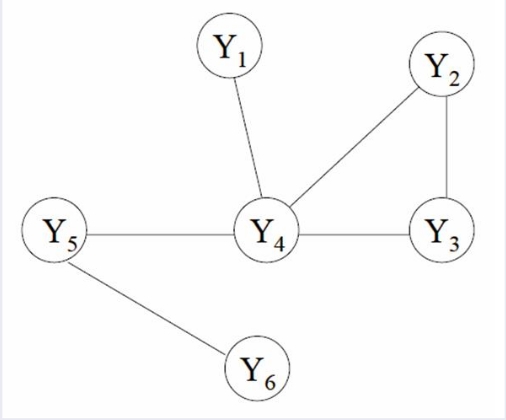
那么,如果这个模型满足
那么V就是一个条件随机场。比如在这幅图里面,既然是条件随机场,那么下列式子就会成立
有朋友看到这里会问,你这个图不是标准的因子图啊?对,实际上对于符合条件随机场的图结构可能是多种多样的,因为它本质上就是对label序列条件独立性质的建模。不过对于条件随机场来说,我们更倾向于用下面这幅图来当作其示意图:
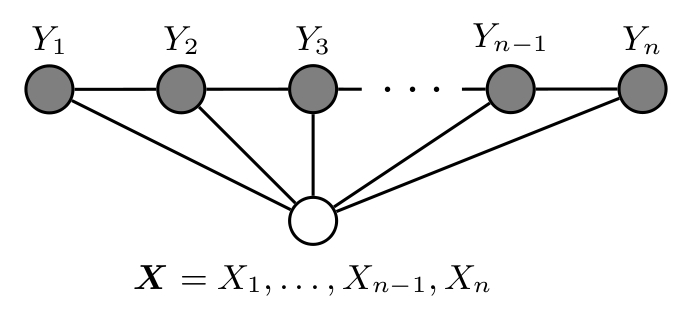
一个条件随机场,属于马尔可夫随机域,它一定符合下面三种等价的马尔可夫独立性:
- 相邻马尔可夫特性:不相邻的两个随机变量定点Vi和Vj对Xi和Xj是否独立,取决于其他所有的随机变量。
- 局部马尔可夫特性:在给定相邻顶点时,对应的任意随机变量Xi与其他所有的随机变量独立
- 全局马尔可夫特性:如果i和j是两个被分离的不相交的顶点,那么对应的随机变量集Xi和Xj在给定其他集合的随机变量时条件独立
好,示意图和性质给出来了,如何去对其分析并推导条件随机场算法呢?之前的文章中,我们讲过conditional independence graph,根据conditional independence的定义,在图中,如果两个顶点之间没有边,我们可以称这两个顶点所代表的随机变量在给定其他所有随机变量时是条件独立的,也就是 全局马尔可夫特性。通俗点讲,就是缺少一条边,就存在一个独立的随机关系。在这种情况下,条件随机场图可以看成是把Y中的所有元素Yv的联合概率分布因式 分解成多个势函数(potential function)的归一化积,其中每一个势函数都会作用于相邻的顶点对Yi和Y(i+1)。归一化的目的,自然就是确保势函数的积是在G中各个随机变量 顶点上有效的概率分布。
注:应一些朋友要求把势函数再讲一下。我们说像上图这种链式CRF的情况,可以把势函数理解为联合概率密度的归一化分解因子,势函数的作用域都是图的一个最大分团(Maxima clique)。 每一个学过图论的朋友都应该听说过clique这个概念,对于给定图G=(V,E)。其中,V={1,…,n}是图G的顶点集,E是图G的边集。图G的团 就是一个两两之间有边的顶点集合。如果一个团不被其他任一团所包含,即它不是其他任一团的真子集,则称该团为图G的极大团(maximal clique)。顶点最多的极大团,称之为图G的最大团(maximum clique)。请参见WIKI解释。实际上,理论上讲,如果不是链式CRF,那么势函数表示的就是一个图中的每一个团,而不是最大团。
学术化一点讲,势函数是一个表示其对应的clique状态的非负实值函数,表征的是该clique的状态。举个例子,对于马尔可夫网络来说,其联合概率分布可以看成
这里的x(k)就表示第k个clique的状态,或者说是出现在这个clique之中的变量的状态。
对于一个图中的每一个clique来讲,它有一个状态,用势函数表示,状态则是由多个feature的加权和构成,因为一个clique是包含多个 节点的,每个节点,其对应的随机变量,都会对应一个feature。文章后面就会提到,我们分析时候选用最简单的二元模型来当作每一点的feature。
既然条件随机场是可以因式分解成势函数的乘积的,那么想推导出条件随机场模型,就应该从势函数入手。在条件随机场模型算法的开山之作 Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data中,作者定义,在指定观察序列X的情况下,一个特定的label序列Y的概率可以被定义为势函数的归一化集,势函数的表达形式为
其中,是整个观察序列以及label序列中处于i和i-1处的label的转移特征函数,
是整个观察序列以及在i处label的状态特征函数。还有Lambda和Mu两个变量是训练估计的参数。对于特定的y和x序列来说,或者处于转移状态,或者处于保持状态。
接下来,和分析最大熵模型一样,我们选取最简单的特征函数来分析,比如下面这个
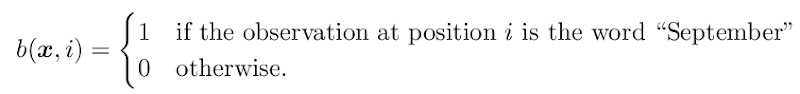
最简单的二元模型。那么转移函数可以定义成这样
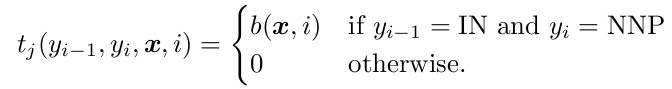
如果y(i-1)和yi都取到特定值的话,就是1,否则就是0。
为了方便表示,我们设定状态特征函数
这样,我们可以定义关于x,y的全局函数
其中函数f可能是状态函数或者转移函数,取决于具体的i。
好,最后一步,就是推导出在给定观察序列x的情况下,label序列y的条件概率:
其中Z(x)是归一化函数
而势函数则表示为
以上就是最简单的线性链式CRF模型
的推导过程。
在本系列中篇一文中,我们介绍过最大熵的最后推导模型是:
看出来和条件随机场模型的差别了么?是不是和本文开头两者的关系是一样的?
也许有朋友会问,你这是假设当前状态只和前一状态有关,或者就是完全独立,这只是一阶的线性链式条件随机场,如果阶数变高了呢?
没关系,我们看,之前定义的f特征函数形式是
而这个公式的通用形式是
其中
咱们刚才讨论的是一阶,此时k=2,如果k>2的话,就是高阶情况了,带进去即可。
对于线性链式条件随机场,使用的时候有两个关键问题
- 训练:给定一个label序列y,观察序列x,如果找到让
取值最大的
?比较常用的有L-BFGS算法,Max Margin算法,Gradient Tree Boosting算法等。
- 推断:如果我们给定了观察序列x,以及参数在求解未知label的时候,需要搜索以最大概率fit的label序列,怎么找?在线性链式CRF上,比较常用的是Viterb算法和Forward-Backward算法。这个隐马尔可夫模型的问题原则上是一样的。
这里提供一个在训练的时候求参数的思路,求最大似然估计极值。我们假设training data集是,则求下列函数的极值。
其中后面一项是为了避免overfitting而加的penalization,前项p(y|x)文章前面已经给出计算公式。前项用对数的原因是简
化运算,因为最大化一个似然函数同最大化它的自然对数是等价的。因为自然对数log是一个连续且在似然函数的值域内严格递增的函数。之后用微分法求最大值
时的取值。
条件随机场是一个很难讲透彻的模型,虽然提出没几年,但是现在的应用已经越来越广泛了。如果有朋友有兴趣深入学习这个模型,可以随意围观这个网站。
好,终于到最后了。总结一下。
在中篇中,我首先介绍了普贝和隐马模型。隐马模型针对朴素贝叶斯来说,优点就是考虑到了状态变量(Label)之间的联系。两者最大的缺点,就是由 于其输出独立性假设,导致其不能考虑上下文的观察特征的关系,限制了观察特征的选择。注意,并不是说普贝和隐马不能处理非独立观察序列,根本原因在于,它 们都是generative模型,都针对联合概率密度建模。要知道,X和Y是贯穿整个观察和标注序列的随机变量,你要针对他们来求联合概率密度,就不得不 考虑对所有变量进行枚举,这在一个长序列中几乎是不现实的,所以才会有假设输出独立的情况。
而以CRF为代表的discriminative模型则解决了这个问题,包括最大熵,以及结合了最大熵的隐马模型,因为他们使用的是定义条件概率 p(y|x)的模型,关注的是,在给定一个特定的观察序列下,label序列的条件概率,这就避免了联合分布中还要考虑观察序列的概率问题。
但不管是对于最大熵也好,还是最大熵隐马也好,由于其在每一节点都要进行归一化,所以只能找到局部的最优值,同时,包括它们在内的所有条件型改良马尔可夫模型,都存在也标记偏置的问题(label bias),简单说就是凡是训练集中未出现的情况全都忽略掉 。
条件随机场则很好的解决了上面这些问题,首先它考虑了全序列的状态变量和观察变量,其次它并不在每一个节点进行归一化,而是所有特征进行全局归一 化,因此可以求得全局的最优值。你说这么好的模型有啥缺点呢?由于处理范围大,参数估计的收敛就会变慢,迭代的复杂度也会变高,要是你处理的不是链式模 型,那么复杂度就更高了。
到这里,动态模型的几种常用建模方法就介绍完了。其实还有不少经典方法没有涉及,比如神经网络,这个有兴趣的朋友自行研究吧。万变不离其中,目前的 方法或者属于generative model,或者属于discriminative model,各有优劣,选取的时候要根据自己的应用取舍。
××××××××××××××××××××××××××××××
系列链接:


