张量的定义

线性代数与矩阵

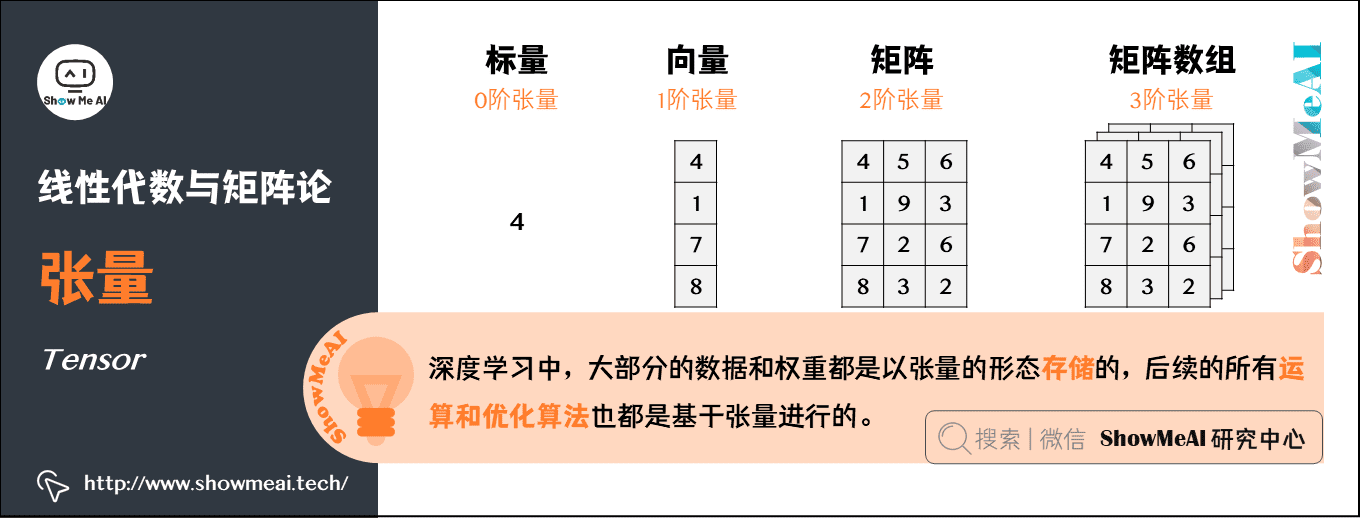
张量（Tensor）

几何代数中定义的张量，是基于向量和矩阵的推广。

• 标量，可以视为零阶张量
• 向量，可以视为一阶张量
• 矩阵，可以视为二阶张量

• 图片以矩阵形态表示：将一张彩色图片表示成一个 的三阶张量，其中 是高， 是宽， 通常取 ，表示彩色图 个颜色通道。
• 在这个例子的基础上，将这一定义继续扩展，即：用四阶张量（样本，高度，宽度，通道）表示一个包含多张图片的数据集，其中，样本表示图片在数据集中的编号。
• 用五阶张量（样本，帧速，高度，宽度，通道）表示视频。

AI中的应用：张量是深度学习中一个非常重要的概念，大部分的数据和权重都是以张量的形态存储的，后续的所有运算和优化算法也都是基于张量进行的。

目前我的知识储备仍停留在二阶张量上。