电荷和场
关键方程
| 说明 |
方程 |
| Coulomb's law 库仑定律 |
\(\vec{\mathbf{F}}_{12} = \dfrac{1}{4\pi\varepsilon_0}\dfrac{q_1q_2}{r_{12}^2}\hat{\mathbf{r}}_{12}\) |
| 无限导线的电场 |
\(\vec{\mathbf{E}}(z)=\dfrac{1}{4\pi\varepsilon_0}\dfrac{2\lambda}{z}\hat{\mathbf{k}}\) |
| 无限平面的电场 |
\(\vec{\mathbf{E}}=\dfrac{\sigma}{2\varepsilon_0}\hat{\mathbf{k}}\) |
| 电偶极矩 Electric Dipole moment |
\(\vec{\mathbf{p}}=q\vec{\mathbf{d}}\) |
| 外部电场中电偶极子上的扭矩 Torque |
\(\vec{\mathbf{\tau}}=\vec{\mathbf{p}}\times\vec{\mathbf{E}}\) |
电偶极子(Electric dipoles)
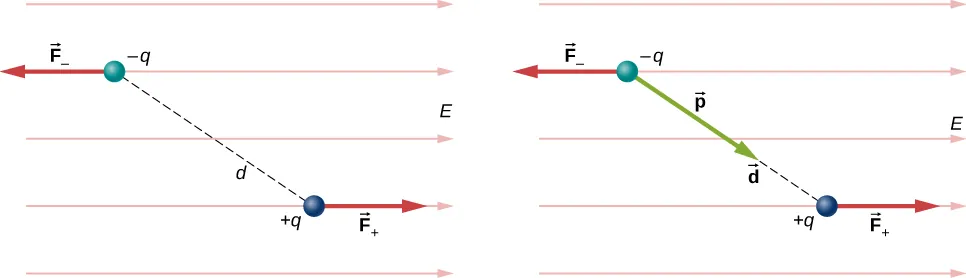
偶极矩 定义为: \(\vec{p} = q\vec{d}\)，其中 \(q\) 为电荷量，\(\vec{d}\) 为电荷间距
外部电场中偶极子上的扭矩为: \(\vec{\tau} = \vec{p} \times \vec{E}\)，其中 \(\vec{E}\) 为电场强度
电偶极子的电场为: \(\vec{E} = \dfrac{-1}{4\pi\varepsilon_0}\left(\dfrac{\vec{p}}{r^3}\right)\)
高斯定律
关键方程
| 说明 |
方程 |
| 均匀电场的电通量 flux |
\(\Phi = \vec{\mathbf{E}}\cdot\vec{\mathbf{A}}\) |
| 通过开放曲面的电通量 |
\(\Phi = \displaystyle\int_{S} \vec{\mathbf{E}}\cdot\hat{\mathbf{n}}dA = \displaystyle\int_{S} \vec{\mathbf{E}}\cdot d\vec{\mathbf{A}}\) |
| 通过封闭曲面的电通量 |
\(\Phi = \displaystyle\oint_{S} \vec{\mathbf{E}}\cdot\hat{\mathbf{n}}dA = \displaystyle\oint_{S} \vec{\mathbf{E}}\cdot d\vec{\mathbf{A}}\) |
| 高斯定律 |
\(\displaystyle\oint_{S} \vec{\mathbf{E}}\cdot \hat{\mathbf{n}}dA = \dfrac{q_{enc}}{\varepsilon_0}\) |
| 导体表面外的电场 |
\(E = \dfrac{\sigma}{\varepsilon_0}\) |
电势
关键方程
| 说明 |
方程 |
| 双电荷系统的势能 |
\(\displaystyle U(r) = k\dfrac{q_1q_2}{r}\) |
| 电势差 |
\(\Delta V = \dfrac{\Delta U}{q}\) |
| 电势 |
\(\displaystyle V=\dfrac{U}{q} = -\int_{R}^{P} \vec{\mathbf{E}}\cdot d\vec{\mathbf{l}}\) |
| 两点之间的电势差 |
\(\displaystyle V_{BA} = -\int_{A}^{B} \vec{\mathbf{E}}\cdot d\vec{\mathbf{l}} = V_B - V_A\) |
| 点电荷的电势 |
\(\displaystyle V = \dfrac{1}{4\pi\varepsilon_0}\dfrac{q}{r} = \dfrac{kq}{r}\) |
| 电偶极矩 |
\(\vec{\mathbf{p}}=q\vec{\mathbf{d}}\) |
| 电偶极子的电势 |
\(\displaystyle V = \dfrac{1}{4\pi\varepsilon_0}\dfrac{\vec{\mathbf{p}}\cdot\hat{\mathbf{r}}}{r^2}\) = \(k\dfrac{\vec{\mathbf{p}}\cdot\hat{\mathbf{r}}}{r^2}\) |
| 连续电荷分布的电势 |
\(\displaystyle V_P = \dfrac{1}{4\pi\varepsilon_0}\displaystyle\int \dfrac{dq}{r} = k\displaystyle\int \dfrac{dq}{r}\) |
| 电场作为电势梯度 |
\(\vec{\mathbf{E}} = -\vec{\mathbf{\nabla}}V\) |
| 笛卡尔坐标中的 Nabla 算子 |
\(\vec{\mathbf{\nabla}} = \hat{\mathbf{i}}\dfrac{\partial}{\partial x} + \hat{\mathbf{j}}\dfrac{\partial}{\partial y} + \hat{\mathbf{k}}\dfrac{\partial}{\partial z}\) |
| 柱坐标中的 Nabla 算子 |
\(\vec{\mathbf{\nabla}} = \hat{\mathbf{r}}\dfrac{\partial}{\partial r} + \hat{\mathbf{\theta}}\dfrac{1}{r}\dfrac{\partial}{\partial \theta} + \hat{\mathbf{k}}\dfrac{\partial}{\partial z}\) |
| 球坐标中的 Nabla 算子 |
\(\vec{\mathbf{\nabla}} = \hat{\mathbf{r}}\dfrac{\partial}{\partial r} + \hat{\mathbf{\theta}}\dfrac{1}{r}\dfrac{\partial}{\partial \theta} + \hat{\mathbf{\varphi}}\dfrac{1}{r\sin\theta}\dfrac{\partial}{\partial \varphi}\) |
电容
关键方程
| 说明 |
方程 |
| 电容 Capacitance |
\(\displaystyle C = \dfrac{Q}{V}\) |
| 平行板电容器(parallel-plate capacitor)的电容 |
\(\displaystyle C = \dfrac{\sigma A}{Ed} = \varepsilon_0\dfrac{ A}{d}\) |
| 真空球形电容器(vacuum spherical capacitor)的电容 |
\(\displaystyle C = 4\pi\varepsilon_0\dfrac{R_1R_2}{R_2-R_1}\) |
| 真空圆柱体电容器(vacuum cylindrical capacitor)的电容 |
\(\displaystyle C = 2\pi\varepsilon_0\dfrac{l}{\ln\dfrac{R_2}{R_1}}\) |
| 串联电容器的电容 |
\(\displaystyle \dfrac{1}{C} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \cdots + \dfrac{1}{C_n}\) |
| 并联电容器的电容 |
\(\displaystyle C = C_1 + C_2 + \cdots + C_n\) |
| 能量密度 |
\(\displaystyle u_E = \dfrac{1}{2}\varepsilon_0E^2\) |
| 电容器的能量 |
\(\displaystyle U_C = \dfrac{1}{2}CV^2 = \dfrac{1}{2}QV = \dfrac{1}{2}\dfrac{Q^2}{C}\) |
| 带电介质的电容器电容 |
\(\displaystyle C = \kappa C_0\) |
| 带电介质的电容器能量 |
\(\displaystyle U = \dfrac{1}{\kappa}U_0\) |
| 介电常数 Dielectric constant |
\(\displaystyle \kappa = \dfrac{E_0}{E}\) |
| 电介质中的感应电场 |
\(\displaystyle \vec{\mathbf{E}}_i=(\dfrac{1}{\kappa}-1)\vec{\mathbf{E}}_0\) |
易错问题
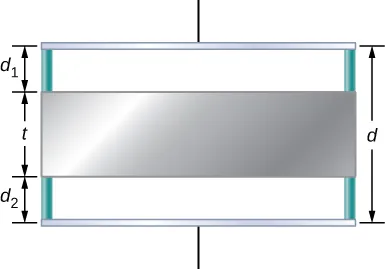
如图，一个金属板插入两个电容器板中，此时计算电容应该直接忽略中间的金属导体高度，答案为
\[C = \varepsilon_0\dfrac{A}{d_1+
\]
电流和电阻
关键方程
| 说明 |
方程 |
| 电流 |
\(\displaystyle I = \dfrac{dQ}{dt}\) |
| 漂移速度 drift velocity |
\(\displaystyle v_d = \dfrac{I}{nqA}\) |
| 电流密度 |
\(\displaystyle I = \iint \vec{\mathbf{J}}\cdot d\vec{\mathbf{A}}\) |
| 电阻率 resistivity |
\(\displaystyle \rho = \dfrac{E}{J} = \dfrac{E}{\sigma E} = \dfrac{1}{\sigma}\) |
| 电阻率和温度的关系 |
\(\displaystyle \rho = \rho_0[1+\alpha(T-T_0)]\) |
| 电阻 |
\(\displaystyle R = \rho \dfrac{L}{A} \equiv \dfrac{V}{I}\) |
直流电路
关键方程
| 说明 |
方程 |
| 路端电压 |
\(\displaystyle V_{terminal} = \varepsilon - Ir_{eq}\) |
| 交汇点原则 Junction rule |
\(\displaystyle \sum I_{in} = \sum I_{out}\) |
| 循环原则 Loop rule |
\(\displaystyle \sum V_{loop} = 0\) |
| 时间常数 |
\(\tau = RC\) |
| 电容器充电的电荷 |
\(q(t) = C\varepsilon(1-e^{-\frac{t}{RC}}) = Q(1-e^{-\frac{t}{\tau}})\) |
| 电容器放电的电荷 |
\(q(t) = Qe^{-\frac{t}{RC}} = Qe^{-\frac{t}{\tau}}\) |
| 电容器放电的电流 |
\(I(t) = \dfrac{dq}{dt} = -\dfrac{Q}{RC}e^{-\frac{t}{RC}} = -\dfrac{Q}{RC}e^{-\frac{t}{\tau}}\) |
磁力和磁场
关键方程
| 说明 |
方程 |
| 洛伦兹力 |
\(\displaystyle \vec{\mathbf{F}} = q(\vec{\mathbf{v}}\times\vec{\mathbf{B}})\) |
| 粒子在磁场中的路径半径 |
\(\displaystyle r = \dfrac{mv}{qB}\) |
| 粒子在磁场中的运动周期 |
\(\displaystyle T = \dfrac{2\pi m}{qB}\) |
| 均匀磁场中载流直导线受力 |
\(\displaystyle \vec{\mathbf{F}} = I\vec{\mathbf{l}}\times\vec{\mathbf{B}}\) |
| 磁偶极矩 magnetic dipole moment |
\(\displaystyle \vec{\mathbf{\mu}} = NIA\hat{\mathbf{n}}\) |
| 电流环路上的扭矩 |
\(\displaystyle \vec{\mathbf{\tau}} = \vec{\mathbf{\mu}}\times\vec{\mathbf{B}}\) |
| 磁偶极子的能量 |
\(\displaystyle U = -\vec{\mathbf{\mu}}\cdot\vec{\mathbf{B}}\) |
| 霍尔电位 |
\(\displaystyle V = \dfrac{IBl}{neA} = Blv_d\) |
| 质谱仪中的电荷质量比 |
\(\displaystyle \dfrac{q}{m} = \dfrac{E}{BB_0R}\) |
| 回旋加速器中的粒子最大速度 |
\(\displaystyle v_{max} = \dfrac{qBR}{m}\) |
磁场的来源
关键方程
| 说明 |
方程 |
| Biot-Savart 定律 |
\(\displaystyle \vec{\mathbf{B}} = \dfrac{\mu_0}{4\pi} \int \dfrac{Id\vec{\mathbf{l}}\times\hat{\mathbf{r}}}{r^2}\) |
| 长直导线的磁场 |
\(\displaystyle \vec{\mathbf{B}} = \dfrac{\mu_0I}{2\pi r}\hat{\mathbf{\theta}}\) |
| 平行电流之间的力 |
\(\displaystyle \dfrac{F}{l} = \dfrac{\mu_0I_1I_2}{2\pi r}\) |
| 电流环路中心的磁场 |
\(\displaystyle B = \dfrac{\mu_0I}{2R}\) |
| 安培环路定理 |
\(\displaystyle \oint \vec{\mathbf{B}}\cdot d\vec{\mathbf{l}} = \mu_0I_{enc}\) |
| 螺线管的磁场 |
\(\displaystyle B = \mu_0nI\) |
| 环形管的磁场 |
\(\displaystyle B = \dfrac{\mu_0NI}{2R}\) |
| 磁导率 |
\(\displaystyle \mu = (1+\chi)\mu_0\) |
电磁感应
关键方程
| 说明 |
方程 |
| 磁通量 |
\(\displaystyle \Phi_m = \int_S \vec{\mathbf{B}}\cdot \hat{\mathbf{n}}dA\) |
| 法拉第电磁感应定律 |
\(\displaystyle \varepsilon = -\dfrac{d\Phi_m}{dt}\) |
| 动生电动势 Motionally induced emf |
\(\displaystyle \varepsilon = Blv\) |
| 环路运动电动势 |
\(\displaystyle \varepsilon = \oint \vec{\mathbf{E}}\cdot d\vec{\mathbf{l}} = -\dfrac{d\Phi_m}{dt}\) |
| 发动机产生的电动势 |
\(\displaystyle \varepsilon = NBA\omega\sin\omega t\) |
电感(Inductance)
关键方程
| 说明 |
方程 |
| 磁通量互感 |
\(\displaystyle M = \dfrac{N_2\Phi_{21}}{I_1} = \dfrac{N_1\Phi_{12}}{I_2}\) |
| 电路中的互感 |
\(\varepsilon_1 = -M\dfrac{dI_2}{dt}\) |
| 以磁通量表示的自感 |
\(\displaystyle LI=N\Phi_m\) |
| 以电动势表示的自感 |
\(\displaystyle \varepsilon = -L\dfrac{dI}{dt}\) |
| 螺线管(solenoid)的自感 |
\(\displaystyle L = \dfrac{\mu_0N^2A}{l}\) |
| 环形线圈(toroid)的自感 |
\(\displaystyle L = \dfrac{\mu_0N^2h}{2\pi}\ln\left(\dfrac{R_2}{R_1}\right)\) |
| 电感器的能量 |
\(\displaystyle U = \dfrac{1}{2}LI^2\) |
| RL电路中的I-t关系 |
\(\displaystyle I(t) = \dfrac{\varepsilon}{R}(1-e^{-\frac{t}{\tau_T}})\) |
| RL电路中的时间常数 |
\(\displaystyle \tau_T = \dfrac{L}{R}\) |
| LC电路中的电荷震荡 |
\(\displaystyle q(t) = q_{0}\cos(\omega t + \phi)\) |
| LC电路中的角频率 |
\(\displaystyle \omega = \sqrt{\dfrac{1}{LC}}\) |
| LC电路中的电流震荡 |
\(\displaystyle i(t) = \omega q_{0}\sin(\omega t + \phi)\) |
| RLC电路中的q-t关系 |
\(\displaystyle q(t) = q_{0}e^{-\frac{R}{2L}t}\cos(\omega t + \phi)\) |
| RLC电路中的角频率 |
\(\displaystyle \omega = \sqrt{\dfrac{1}{LC}-\left(\dfrac{R}{2L}\right)^2}\) |
交流电路
关键方程
| 说明 |
方程 |
| 交流电压 |
$ \displaystyle v=V_0\sin\omega t$ |
| 交流电流 |
$ \displaystyle i=I_0\sin\omega t$ |
| 容抗 capacitive reactance |
$ \displaystyle X_C = \dfrac{1}{\omega C}$ |
| 感抗 inductive reactance |
$ \displaystyle X_L = \omega L$ |
| RLC串联电路的相位角 |
\(\displaystyle \tan\phi = \dfrac{X_L-X_C}{R}\) |
| RLC串联电路的阻抗 |
\(\displaystyle Z = \sqrt{R^2+(X_L-X_C)^2}\) |
| 欧姆定律交流版本 |
\(\displaystyle I_0 = \dfrac{V_0}{Z}\) |
| 电流的有效值 |
\(\displaystyle I_{rms} = \dfrac{I_0}{\sqrt{2}}\) |
| 电压的有效值 |
\(\displaystyle V_{rms} = \dfrac{V_0}{\sqrt{2}}\) |
| 电路元件平均功率 |
\(\displaystyle P_{avg} = \dfrac{1}{2}I_0V_0\cos\phi\) |
| 电阻器的平均功率 |
\(\displaystyle P_{avg} = \dfrac{1}{2}I_{0}V_{0}=I_{rms}V_{rms}=I_{rms}^2R\) |
| 电路的谐振角频率(resonant angular frequency) |
\(\displaystyle \omega_0 = \sqrt{\dfrac{1}{LC}}\) |
| 电路的品质函数 |
\(\displaystyle Q = \dfrac{\omega_0L}{R} = \dfrac{1}{\omega_0CR}=\dfrac{\omega_0}{\Delta\omega}\) |
| 变压器的电压比 |
\(\displaystyle \dfrac{V_2}{V_1} = \dfrac{N_2}{N_1}\) |
| 变压器的电流比 |
\(\displaystyle \dfrac{I_2}{I_1} = \dfrac{N_1}{N_2}\) |
电磁波
关键方程
| 说明 |
方程 |
| 位移电流(displacement current) |
\(\displaystyle I_d = \varepsilon_0\dfrac{d\Phi_E}{dt}\) |
| 高斯定律 |
\(\displaystyle \oint \vec{\mathbf{E}}\cdot d\vec{\mathbf{A}} = \dfrac{Q_{in}}{\varepsilon_0}\) |
| 高斯磁定律 |
\(\displaystyle \oint \vec{\mathbf{B}}\cdot d\vec{\mathbf{A}} = 0\) |
| 法拉第定律 |
\(\displaystyle \oint \vec{\mathbf{E}}\cdot d\vec{\mathbf{s}} = -\dfrac{d\Phi_m}{dt}\) |
| 安培-麦克斯韦定律 |
\(\displaystyle \oint \vec{\mathbf{B}}\cdot d\vec{\mathbf{s}} = \mu_0I_{}+\mu_0\varepsilon_0\dfrac{d\Phi_E}{dt}\) |
| 平面电磁波的波动方程 |
\(\displaystyle \dfrac{\partial^2E_y}{\partial x^2} = \varepsilon_0\mu_0\dfrac{\partial^2E_y}{\partial t^2}\) |
| 电磁波的速度 |
\(\displaystyle v = \dfrac{1}{\sqrt{\varepsilon_0\mu_0}} = c\) |
| 电磁场中电场和磁场的比值 |
\(\displaystyle \dfrac{E}{B} = c\) |
| 能量通量矢量(Poynting vector) |
\(\displaystyle \vec{\mathbf{S}} = \dfrac{1}{\mu_0}\vec{\mathbf{E}}\times\vec{\mathbf{B}}\) |
| 电磁波的平均强度 |
\(\displaystyle I=S_{avg} = \dfrac{c\varepsilon_0}{2}E_{max}^2=\dfrac{c\mu_0}{2}B_{max}^2=\dfrac{E_{max}B_{max}}{2\mu_0}\) |
| 完全吸收时的辐射压力 |
\(\displaystyle P = \dfrac{I}{c}\) |
| 完全反射时的辐射压力 |
\(\displaystyle P = \dfrac{2I}{c}\) |
