UCB-CS161 笔记

Memory Safety

Buffer overflow

You should keep only 61C's config (not 161's config), and when SSHing, you need to explicitly type the usernames: ssh cs61c-xyz@hive22 or ssh cs161-xyz@hive22.

ebp always points to sfp.

看以下这个例子

char buf[8];
int authenticated = 0;
void vulnerable() {
    gets(buf);
}

由于 gets(buf) 不会检查，所以可能导致缓冲区溢出

比如如果攻击者可以将 9 个字节的数据写入 buf （第 9 个字节设置为非零值），则会将 authenticated 标志设置为 true，并且攻击者将能够获得访问权限。

被覆盖的也可以是一个指向地址的指针，这样就会在试图跳转到原本指向的地址时跳转到覆写的任何地址上，从而执行一些恶意指令

void func(int len, char *data){
	
}

memcpy 中的 size_n 是 unsigned 的

Cryptography

In a nutshell, cryptography is about communicating securely over insecure communication channels.

Introduction

这里有个攻击 CS61A 考试的 Lab，如果想做的话可以发邮件给 Maddie

几个主要角色:

• Alice and Bob: The main characters trying to send messages to each other over an insecure communication channel (之后还会有 Carol 和 Dave)
• Eve: An eavesdropper who can read any data sent over the channel (也被称为 honest-but-curious attacker)
• Mallory: A manipulator who can read and modify any data sent over the channel (也被称为 malicious attacker)

三大属性:

• Confidentiality(机密性): An adversary cannot read our messages.

• Integrity(完整性): An adversary cannot change our messages without being detected.

• Authenticity(真实性): I can prove that this message came from the person who claims to have written it.

  • 注意真实性依赖于完整性(如果信息被篡改，无论信息来源如何都没有意义)

Roadmap

	Symmetric-key	Asymmetric-key
Confidentiality	One-time pads Block ciphers with chaining modes (e.g. AES-CBC) Stream ciphers	RSA encryption ElGamal encryption
Integrity, Authentication	MACs (e.g. HMAC)	Digital signatures (e.g. RSA signatures)

Define of Security: Security Game

IND-CPA

全称是 indistinguishability under chosen plaintext attack，用来定义 confidentiality

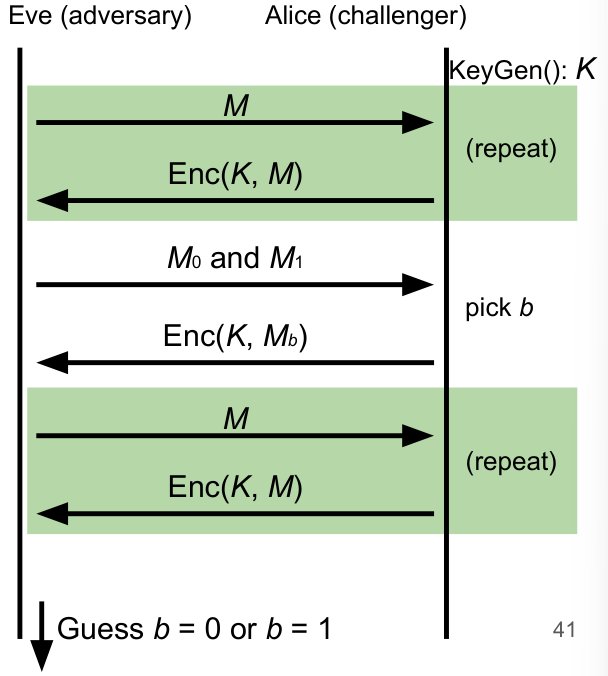
IND-CPA game works as follows:

1. Eve 选择两条不同信息 $M_0$ 和$M_1$，发给 Alice
2. Alice 随机选择一条信息进行加密并发回 Eve
3. Eve 可以任意选择明文并查看 Alice 对其加密的密文(这个操作可以在任意时候重复做)
4. Eve 猜 Alice 加密了哪一条

如果最后 Eve 猜中的概率高于随机猜(也就是一半的概率)，那么这个 scheme 就是不安全的，反之安全

需要注意的几点:

1. $M_0$ 和$M_1$ 长度必须一致，否则将会是一个很 trivial 的情形(直接根据长度判断即可)
   • 因为我们的加密算法必然泄漏长度，否则所有的明文都被映射到有限的相同长度的密文
2. 只需保证 Eve 需要的时间低于多项式时间即可
3. Eve 猜中的概率在可忽略的范围内和 $\dfrac{1}{2}$ 相等即可，比如 $\dfrac{1}{2} + \dfrac{1}{2^{128}}$

EU-CPA

全称是 existential unforgeability under chosen-plaintext attack，用来定义 integrity

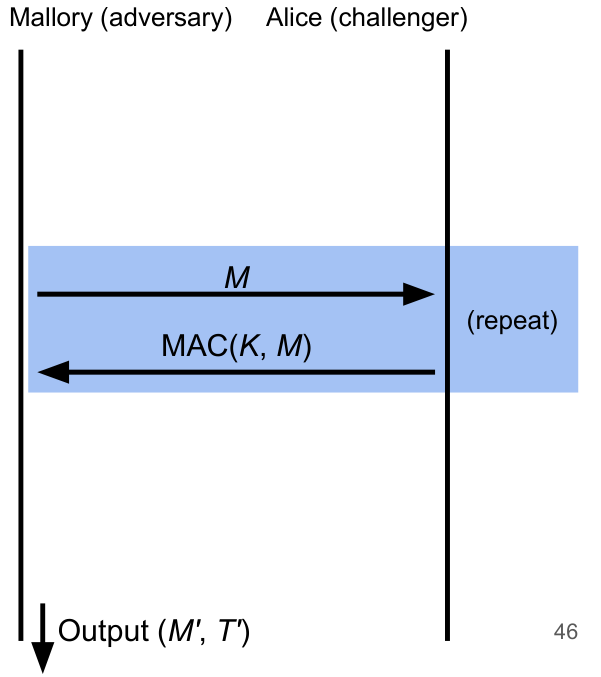
类似于 IND-CPA

1. Mallory may send messages to Alice and receive their tags
2. Eventually, Mallory creates a message-tag pair $(M', T')$
   • $M'$ cannot be a message that Mallory requested earlier
   • If $T'$ is a valid tag for $M'$, then Mallory wins. Otherwise, she loses.

A scheme is EU-CPA secure if for all polynomial time adversaries, the probability of winning is 0 or negligible

Symmetric-Key

A symmetric-key encryption scheme has three algorithms:

• $\text{KeyGen}() → K$: Generate a key $K$

• $\text{Enc}(K, M)$ → $C$: Encrypt a plaintext $M$ using the key $K$ to produce ciphertext $C$

• $\text{Dec}(K, C)$ → $M$: Decrypt a ciphertext $C$ using the key $K$

One-Time Pad

1. Key generation: Alice and Bob pick a shared random key $K$.

2. Encryption algorithm: $C=M⊕K$.

3. Decryption algorithm: $M=C⊕K$.

具有 Confidentiality，但不能重复使用 (Two-Time Pads 只需要再次发送 $M_0$ 或 $M_1$ 其中之一即可确认)

事实上，所有 deterministic 的密码都不是 IND-CPA 安全的，只需如法炮制上述过程即可

Block Cipher

An encryption/decryption algorithm that encrypts a fixed-sized block of bits. ( $n$ bits $\to$ $n$ bits)

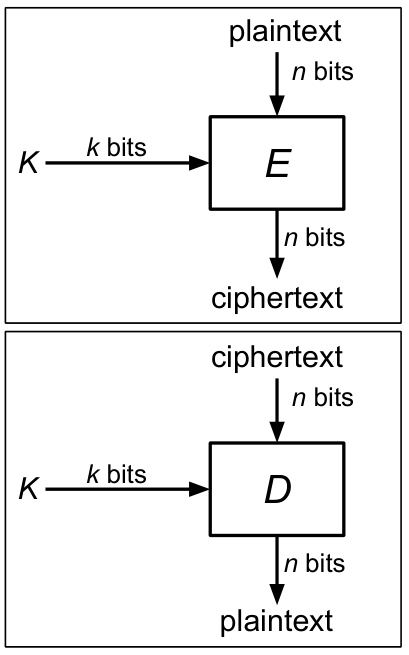
如图，Block Ciphers 要求 $E_K(M)$ 和 $D_K(C)$ 是互逆的函数(即都是双射函数，亦即 $E_K(M)$ 是一个 permutation)，否则我们不可能从密文还原出确定的明文

但是 Block Ciphers 有几个问题:

• 不是 IND-CPA 安全的(使用相同的 $K$ )
  • 可以用 randomized 或者 stateful 的方法来解决
• 只能加密 $n$-bit 的信息
  • 分块，把长信息拆成等长的短信息
  • Padding (PKCS #7 填充，即填充需要填充的字节数，例如 0000000010111 填充为0000000010111333)
    • 如果不需要填充，则直接附加一个新块

---

最常用的 Block Ciphers 就是 AES，但 AES 本身不是 IND-CPA 的(因为其确定性)，所以有以下几种改良版本(操作模式)，注意 $IV$ 不能重复使用，否则会丧失 Confidentiality，但是 $IV$ 被泄漏则不会有影响(**唯一需要保持 secrecy 的只有 $Key$ **)

需要注意的是单独使用以下模式全都会泄露明文长度(要求明文长度不泄露是更强的安全要求)

• ECB(electronic code book) : 简单地进行分组加密，$Enc(K, M) = C_1 || C_2 || … || C_m$

  

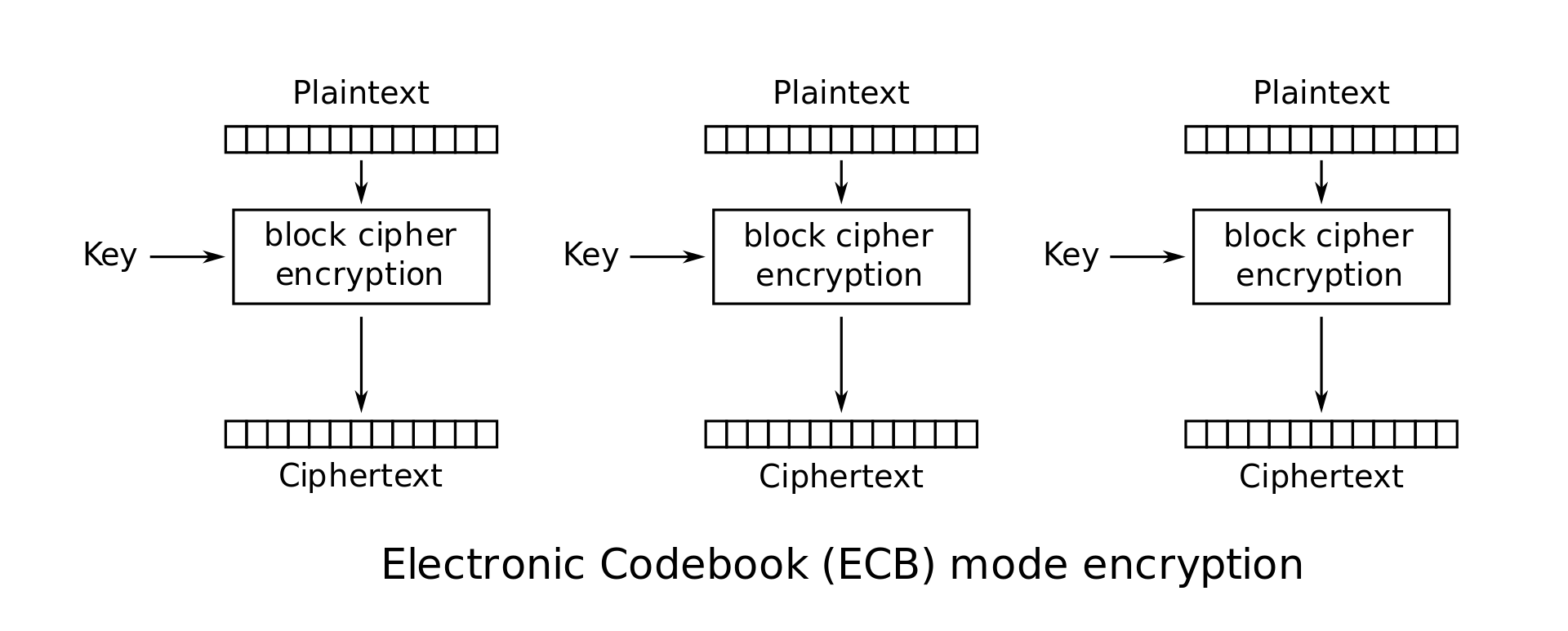
• CBC (Cipher Block Chaining): 是一种 stateful 的方法，并且拥有一个 randomized 的 IV (Initialization Vector)，泄露了 $IV$ 就会全部泄露。

  • Enc: $C_i = E_K(M_i ⊕ C_{i-1})$，$C_0 = IV$

    

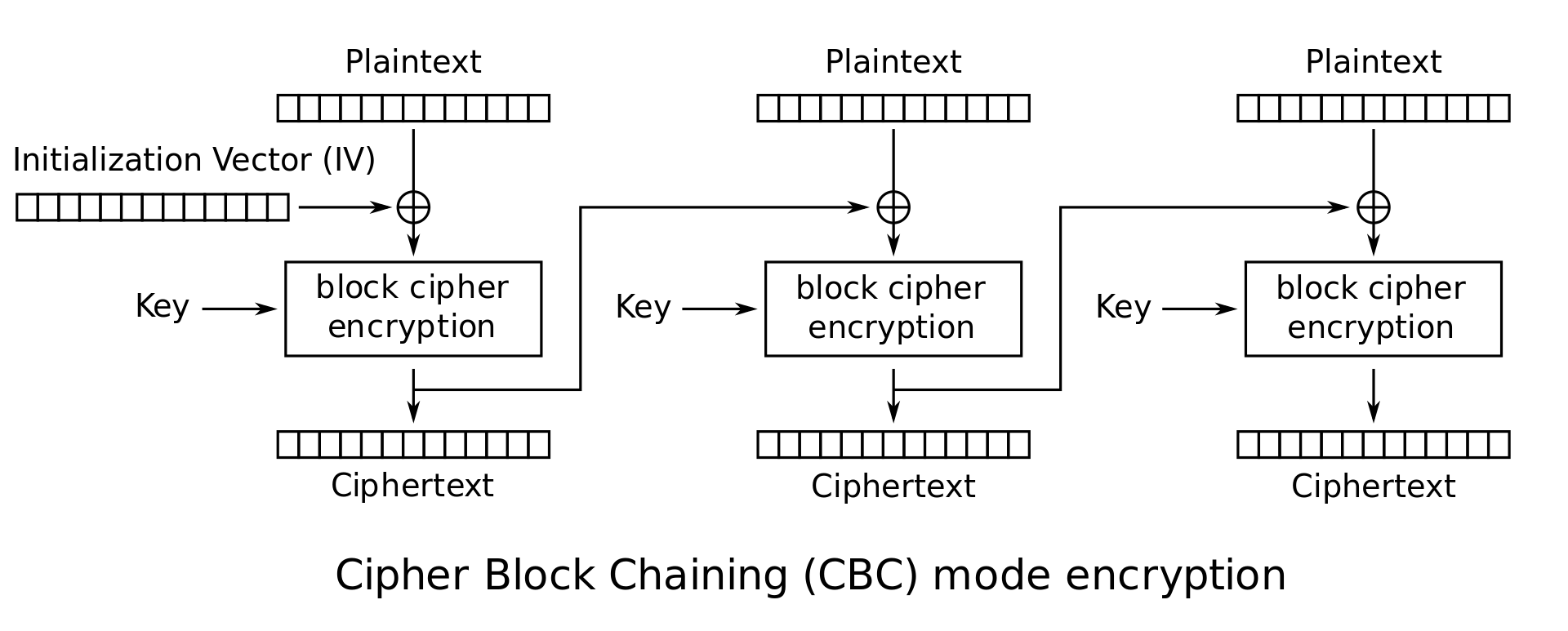
  • Dec: $M_i=D_K(C_i)⊕C_{i−1}$，注意这可以并行化 (Parallelization) 处理

    

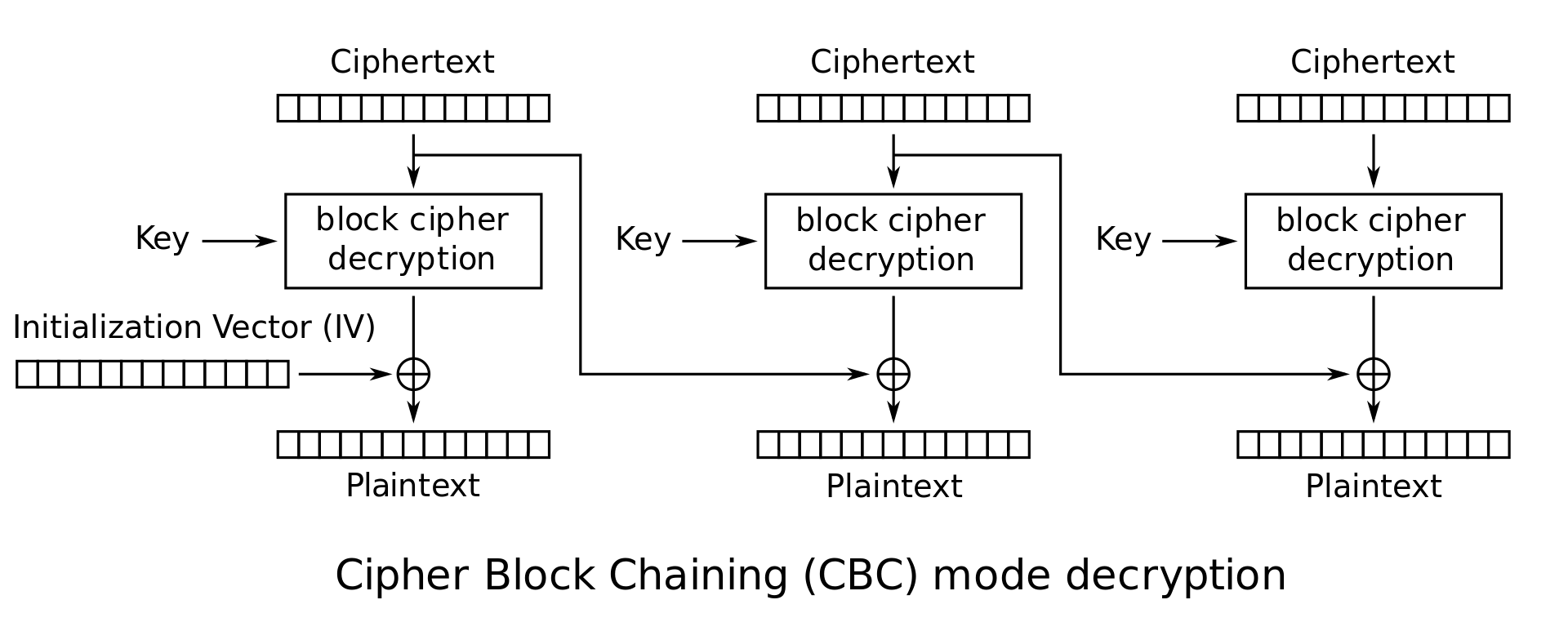
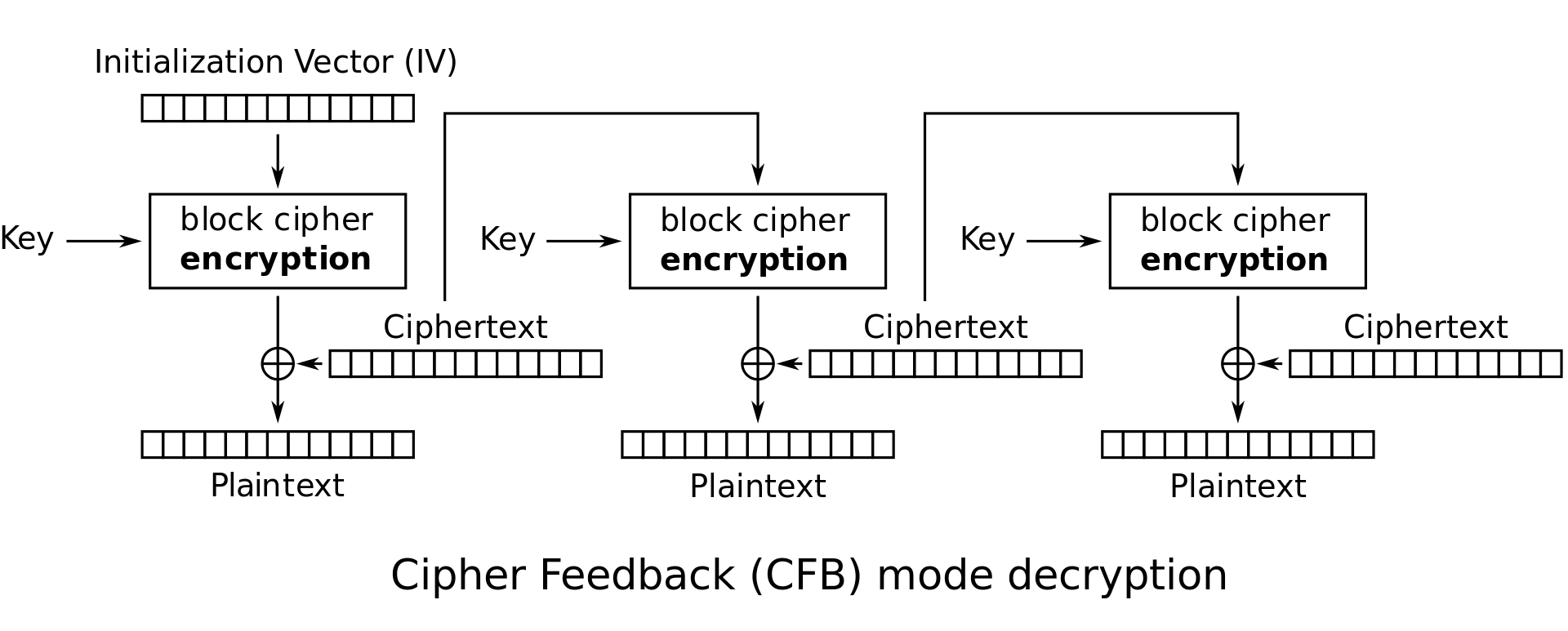
• CFB (Ciphertext Feedback): 注意加密和解密使用的是同一个函数。在这种模式下，加密另一条信息时即使重用 $IV$，也只会泄漏前面一部分，问题不大(事实上，从第一个不同的位置所在的块开始，前面一样是显而易见的)

  • Enc: $C_i = E_K(C_{i-1}) ⊕ M_i$，$C_0 = IV$，不需要 padding

    

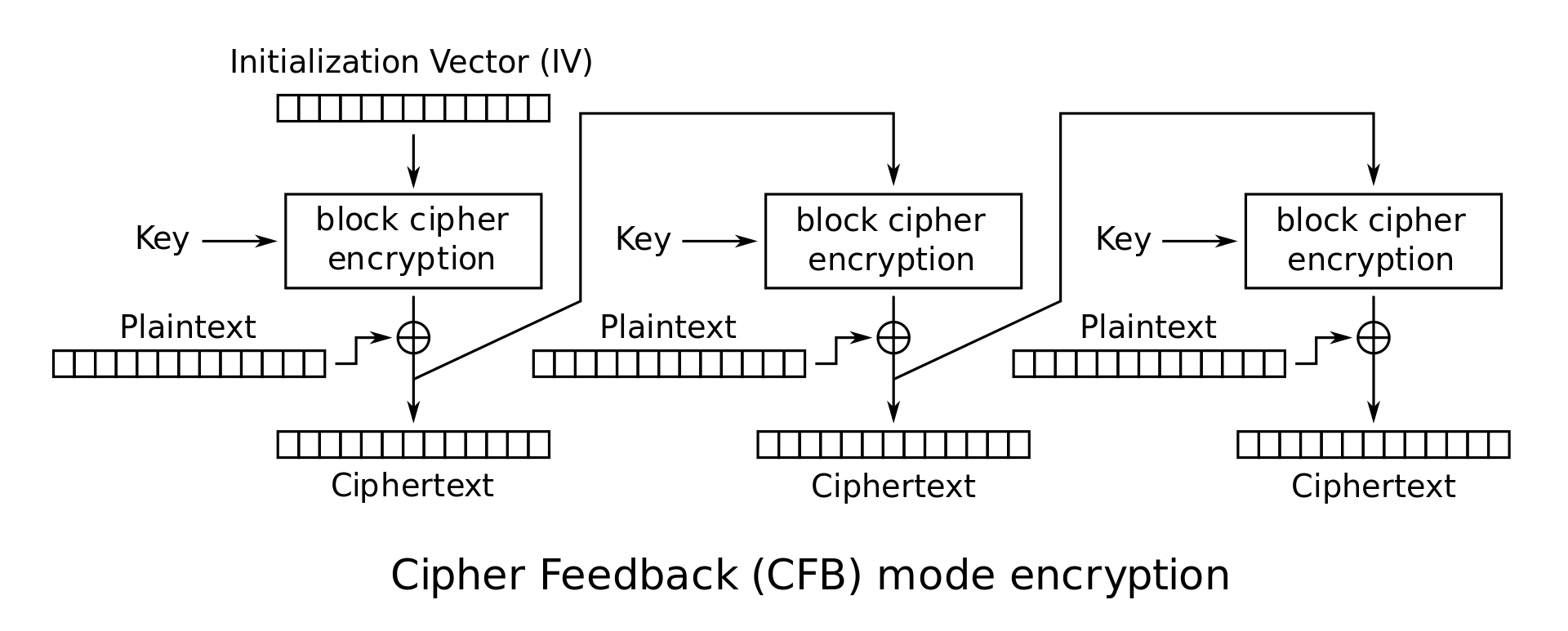
  • Dec: $M_i = E_K(C_{i-1}) ⊕ C_i$，$C_0 = IV$，可以并行化

    

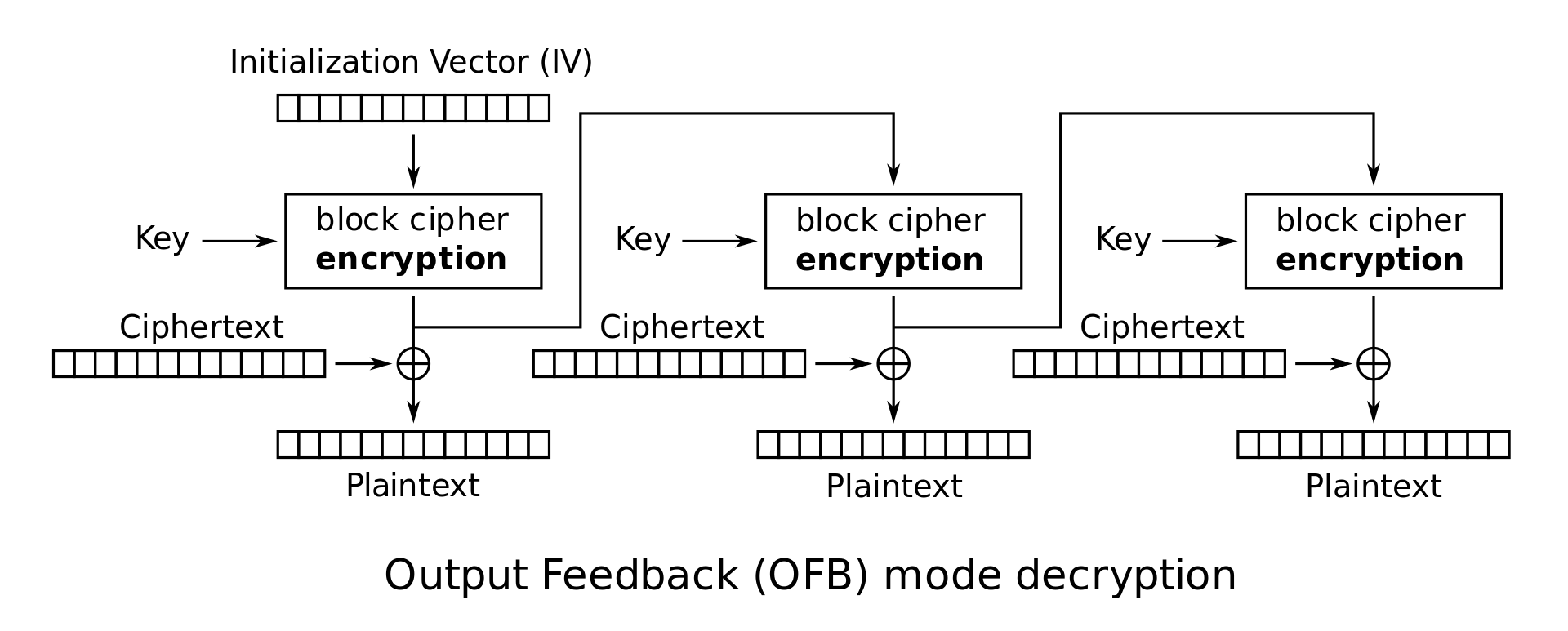
• OFB (Output Feedback): 一直对 $IV$ 进行操作，有 $Z_0=IV$，$Z_i=E_K(Z_{i-1})$

  • Enc: $C_i = Z_i ⊕ M_i$

  

  • Dec: $M_i = Z_i ⊕ C_i$

    

• Counter (CTR): 将 OFB 模式中的 $Z_i$ 替换为 $IV + i$ 即可，此时我们会称 $IV$ 为 $nonce$ (number used once()，这里不再需要 Padding 了，直接异或前一部分即可。方便的同时如果我们重用 $nonce$ 会带来比 OFB 更严重的后果，每个相同位置上的 block 信息都会泄露

  • Enc: $C_i = E_K(IV + i) \oplus M_i$，可以并行化

    

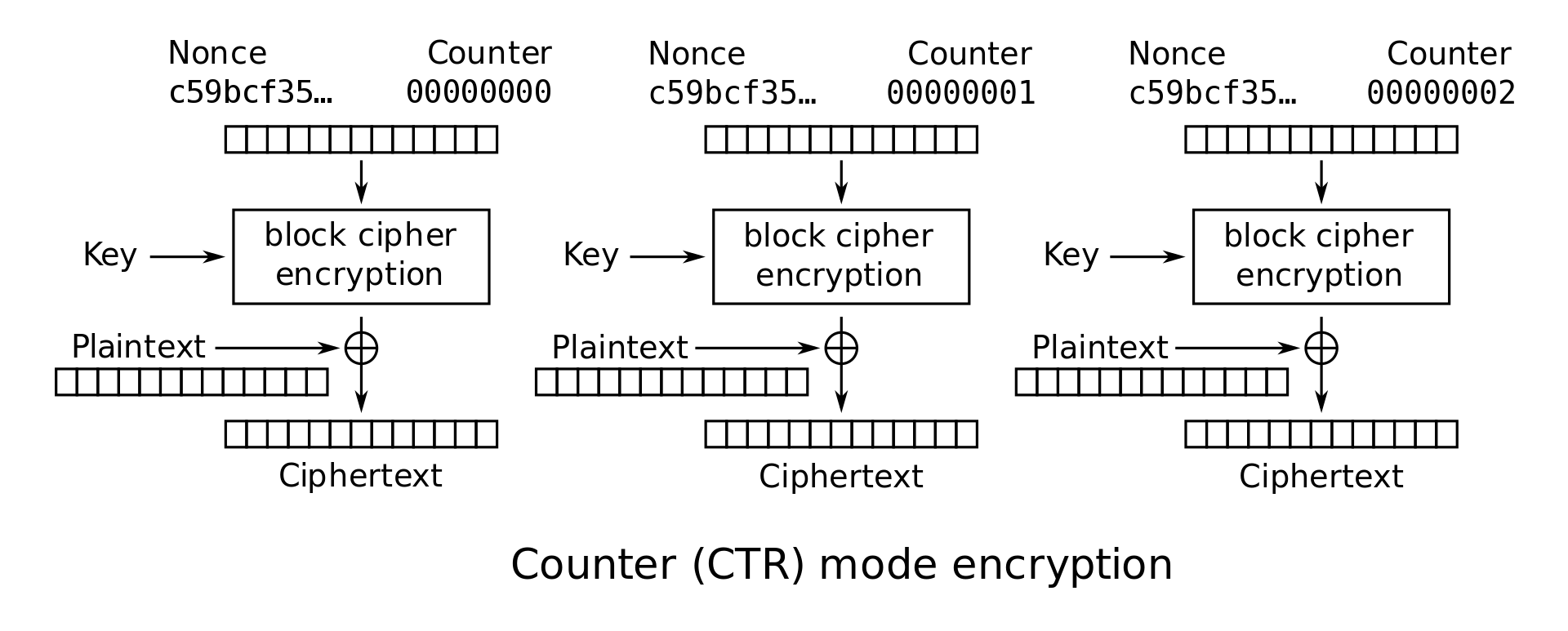
  • Dec: $M_i = E_K(IV + i) \oplus C_i$，可以并行化

    

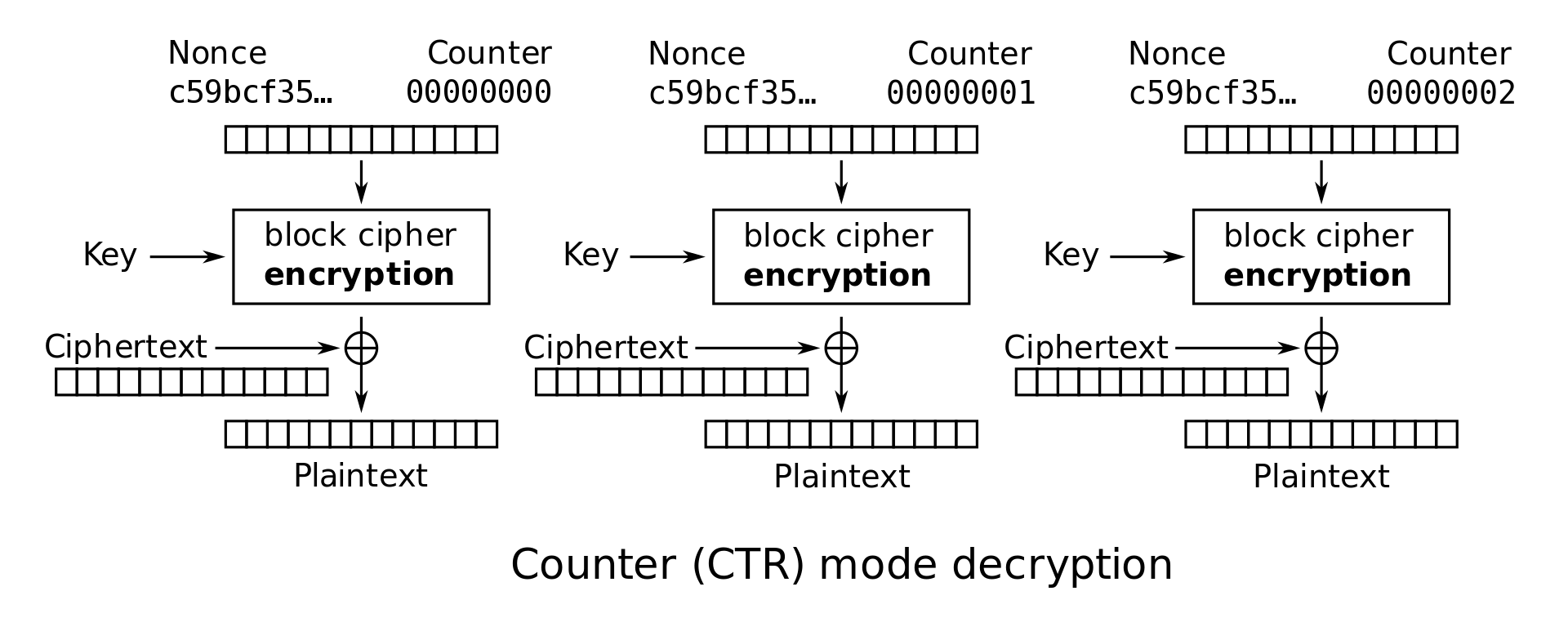
Cryptographic Hash

输入任意长度的信息 $M$ 输出固定长度的 hash 值，也可以写作 $\{0, 1\}^* → \{0, 1\}^n$

几个重要性质：

• One-way-ness (“preimage resistance”): Given an output $y$, it is infeasible to find any input $x$ such that $H(x) = y$

• Collision-resistance: It is infeasible to (i.e. no polynomial time attacker can) find any pair of inputs $x' ≠ x$ such that $H(x) = H(x')$

  • It implies Second preimage resistant: Given an input $x$, it is infeasible to find another input $x'$ such that $x'≠x$ but $H(x)=H(x')$.

• Random/unpredictability: Changing 1 bit in the input causes the output to be completely different (avalanche effect)

在一些威胁模型下可以用来保证 integrity (Mallory 只能改 messages 而不能改 hashes)

MAC

全称是 Message Authentication Codes，MAC 保证 integrity 但不保证 confidentiality

由两部分组成

• $\text{KeyGen}() → K$: Generate a key $K$

• $\text{MAC}(K, M) → T$: Generate a tag $T$ for the message $M$ using key $K$

  • Inputs: A secret key and an arbitrary-length message
  • Output: A fixed-length tag on the message

一个简单的例子是 $\text{NMAC}(K_1, K_2, M) = H(K_1 \Vert H(K_2 \Vert M))$， 其中 $K_1$ 和 $K_2$ 是产生的不相关的随机数且长度一致，均为 hash 输出的长度 $n$

This is for security reasons, because having longer than $n$ bits for a n-bit hash output is redundant (bruteforcing all $n$ bit hashes is more efficient than guessing a key longer than $n$ bits). Technically, the keys need only be the length of the hash block size (but for our purposes, this is usually the same size as the output).

我们可以进一步改进使其只需要一个随机数 $K$，即 $\text{HMAC}(M,K) = H((K' \oplus opad) \Vert H((K' \oplus ipad) \Vert M ))$

其中如果 $K$ 的长度小于 $n$ 补零即可，反之进行一次 Hash，即 $K' = H(K)$

HMAC (其中 H 是 Hash 的意思) 结合了 MAC 和底层哈希的优点。即使有密钥也很难还原出信息。

$opad$ 和 $ipad$ 只需要有一位不同即可，但出于密码工程师的 paranoia，通常将其硬编码为重复的 0x5c 和 0x36 (直到长度等于 $n$)

Authenticated Encryption

定义: A scheme that simultaneously guarantees confidentiality and integrity (and authenticity, depending on your threat model) on a message.(同时保证几大属性)

We need an IND-CPA encryption scheme and an unforgeable MAC scheme

两种方案:

• MAC-then-encrypt: $\text{Enc}(K_1, M || \text{MAC}(K_2, M))$

  • 不好，因为不具备 ciphertext integrity，必须对解密之后才能判断消息是否被篡改，但某些时候运行解密算法是很危险的(因为我们不知道输入的到底是什么)，并且已经被 side channel vectors 方法攻击过

    In a side channel attack, improper usage of a cryptographic scheme causes some information to leak through some other means besides the algorithm itself, such as the amount of computation time taken or the error messages returned.

• Encrypt-then-MAC: $\text{MAC}(K_2, \text{Enc}(K_1, M))$

  • 更常用，因为更 robust

注意，不要 Key Reuse (在两种不同的 scheme 中使用相同的 Key，比如 HMAC 和 Enc)

• 这意味着不同用途 (e.g. computing HMACs on different messages in the same context with the same key) 不是 key reuse

PRNG

即 Pseudorandom Number Generators

PRNG 按照一个确定的算法生成伪随机数(当然如果不知道内部状态的话和真随机数无法区分)，如下:

• PRNG.Seed(randomness): 用真随机数的熵初始化其状态
• PRNG.Generate($m$): 生成 $m$ 个伪随机数

PRNG 具有 rollback-resistant: 抗回滚性，即使了解了当前状态也推不出前面的

用一个 CTR mode就可以实现一个 PRNG

• PRNG.Seed($K | IV$)

• Generate(m) = $E_k(IV|1) | E_k(IV| 2) | E_k(IV|3) … E_k(IV| ceil(m/n))$

Stream Cipher

如果用 PRNG 来生成 one-time pad (当然，要避免 key reuse)，就可以不停地加密解密(一次一位)

• $Enc(K, M) = \langle IV, PRNG(K, IV) \oplus M \rangle$
• $Dec(K, IV, C_2) = PRNG(K, IV) \oplus C_2$

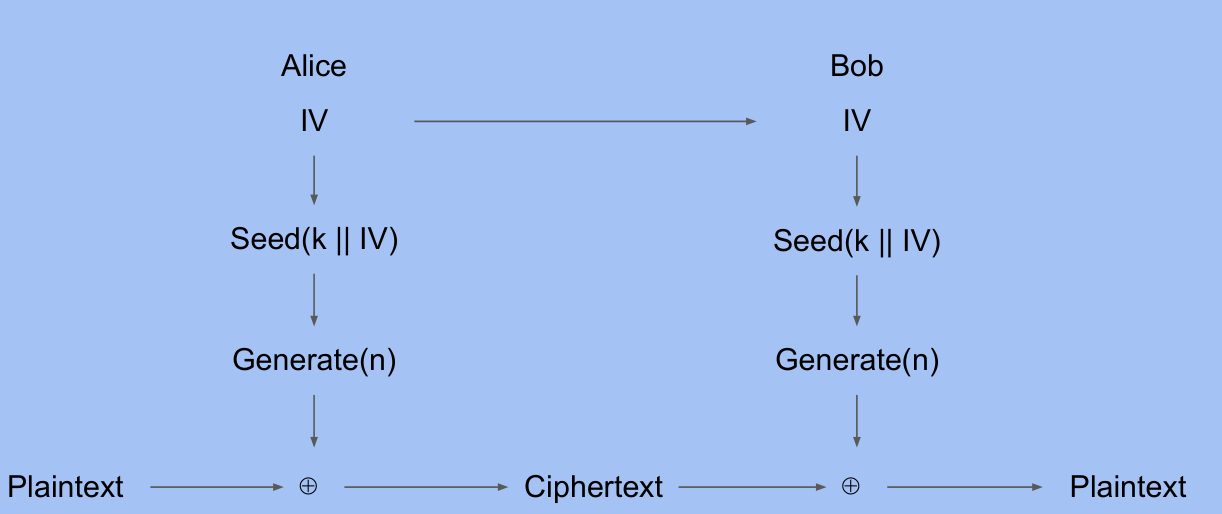
If you squint carefully, AES-CTR is a type of stream cipher, and modes like AES-CBC need padding to function, so doesn’t function well on streams

像 CTR 这种包含计数器的模式的一个很好的性质是能够加密或解密消息中的任意点，而无需从头开始

流密码在输出不是太多的情况下是 IND-CPA 的，具体来说如果 key 有 $n$ 位，输出一般不要超过 $2^{n/2}$

Asymmetric Key (Public Key)

由以下三部分组成，好处是不再需要 Alice 和 Bob 共享密钥，坏处就是慢

• $\text{KeyGen}() → PK, SK$: Generate a public/private keypair, where $PK$ is the public key, and $SK$ is the private (secret) key

• $\text{Enc}(PK, M) → C$: Encrypt a plaintext $M$ using public key $PK$ to produce ciphertext $C$

• $\text{Dec}(SK, C) → M$: Decrypt a ciphertext $C$ using secret key $SK$

依赖于几个问题:

• Discrete logarithm problem
• Diffie-Hellman assumption: 给定 $g$，$p$，$g^a \bmod p$，$g^b \bmod p$，无法在多项式时间内计算出 $g^{ab} \bmod p$

Diffie-Hellman Key Exchange

用于交换密钥 $K = g^{ab}$ (前几节讨论的对称密码都需要共同密钥)，如图所示

• 注意是 Ephemeral: Short-term and temporary, not permanent
  • 交换完成之后这些密钥 $a,b,K$ 不再使用
  • 所以也叫 Diffie-Hellman ephemeral, or DHE

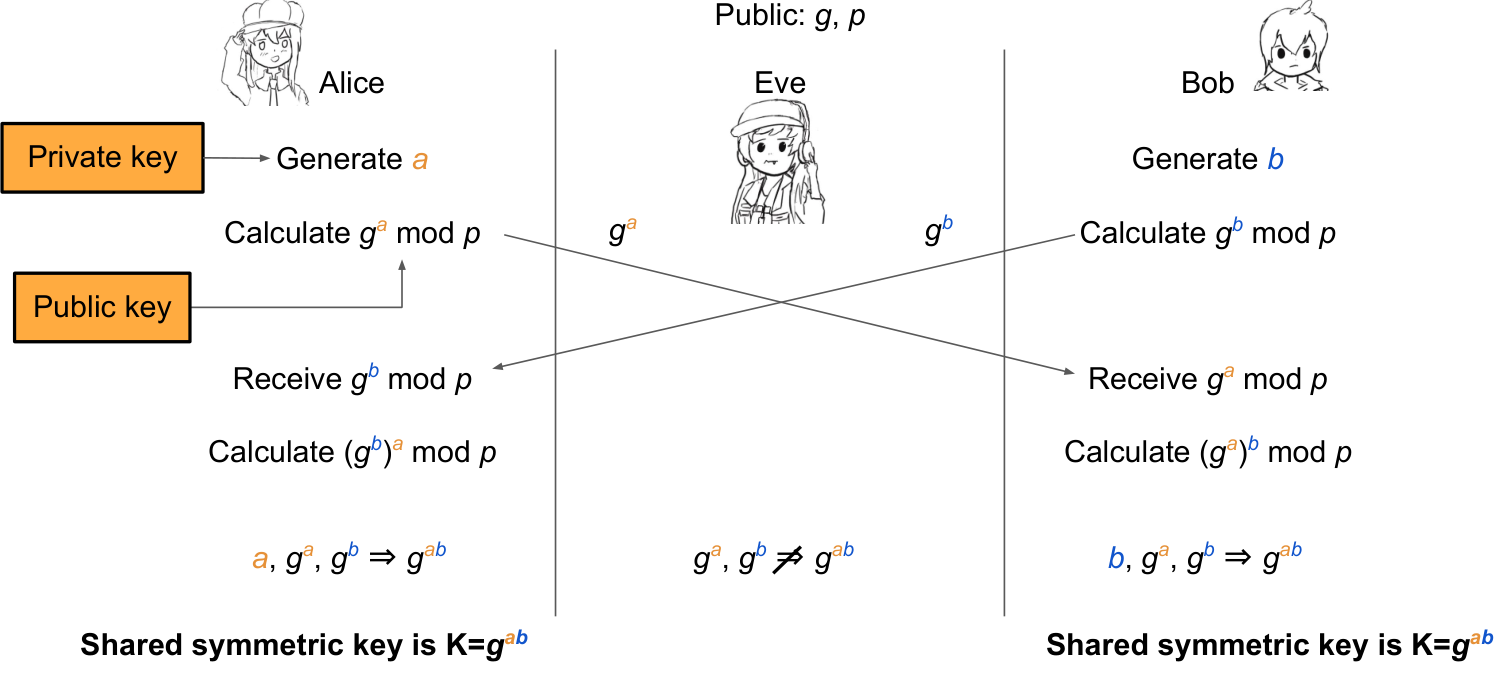
DHE 不保证 authentication!!!，MITM(Man-in-the-middle attack) 攻击如下图

还有一个问题是 active protocol: Alice 和 Bob 必须同时在线(不想一些聊天软件，先把消息发到服务器)

ElGamal Encryption

• $\text{KeyGen}()$: Bob 生成私钥 $b$ 和公钥 $B = g^b \bmod p$

• $\text{Enc}(B, M)$: Alice 生成一个随机的 $r$ 并计算 $R = g^r \bmod p$，然后发送 $C_1 = R$，$C_2 = M × B^r \bmod p$

• $\text{Dec}(b, C_1, C_2)$: Bob 计算 $C_2 × C_1^{-b} = M × B^r × R^{-b} = M × g^{br} × g^{-br} = M \bmod p$

但是问题很大，既没有 confidentiality 也没有 integrity

• confidentiality:攻击者可以发送 $M_0 = 0$，$M_1 ≠ 0$
  • 可以通过加 padding 之类的方法解决
• integrity: ElGamal 具有 Malleability，这意味着攻击者可以发送 $C_1' = C_1$，$C_2' = 2 × C_2 = 2 × M × g^{br}$，看起来就像加密了 $C_2'$ 一样

RSA Encryption

正确性来自数论中的欧拉定理

• $\text{KeyGen}()$:
  1. 随机选择两个大素数 $p$ 和 $q$
  2. 计算公钥 $N=pq$
  3. 随机选择一个与 $(p-1)(q-1)$ 互质的公钥 $e$
  4. 计算私钥 $d=e^{-1} \bmod (p-1)(q-1)$
• $\text{Enc}(e,N,M)$: 输出 $M^e \bmod N$
• $\text{Dec}(d,C)$: 输出 $C^d = M^{ed} \bmod N$

RSA 有几个问题

• deterministic，这意味着没有 confidentiality
• 即使多次发送同一 message 时用不同密钥加密仍然会导致泄露 (使用中国剩余定理)
• 加密时间和 private key 以及 message 相关，利用某些精妙的分析可以获得一些信息

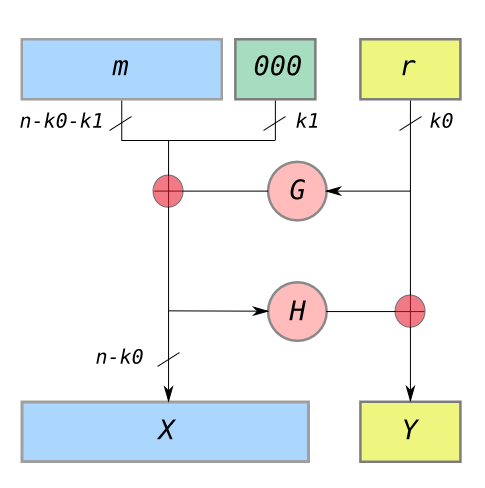
用 OAEP (Optimal asymmetric encryption padding) 可以解决，这会在信息上 pad 一些 randomness，如下，其中 G 和 H 均为 Hash 函数

Digital Signature

以一种 asymmetric 的方式提供 integrity/authenticity ，有三部分

• $\text{KeyGen}() → PK, SK$: Generate a public/private keypair, where $PK$ is the verify (public) key,
  and $SK$ is the signing (secret) key

• $\text{Sign}(SK, M) → sig$: Sign the message $M$ using the signing key $SK$ to produce the signature $sig$

• $\text{Verify}(PK, M, sig) → {0, 1}$: Verify the signature $sig$ on message $M$ using the verify key $PK$ and
  output 1 if valid and 0 if invalid

正确性要求 $\text{Verify}(PK, M, \text{Sign}(SK, M)) = 1$

在实际中，我们先对 $M$ 进行 Hash 再签名

RSA Signature

• $\text{KeyGen}()$: 和 RSA 加密一样
• $\text{Sign}(d, M)$: 计算 $H(M)^d \bmod N$
• $\text{Verify}(e, N, M, sig)$: 验证 $sig^e = H(M) \bmod N$

Certificate

用于解决公钥分发的问题(我们不知道得到的公钥是不是攻击者伪造的!)，主要思想就是 Endorse

另一个方法是 Trust-on-first-use(也叫 Leap-of-Faith): 相信第一次通信时的公钥，并在之后发现更改时发出警告，一个例子就是 SSH

中心化的架构是 Trusted Directory: One server holds all the keys, and everyone has the TD’s
public key

树型结构 Certificate Authorities: 一个 root CA 和很多 intermediate CA

Revocation

• Expiration Date: 给每个 Certificate 都安排一个 Expiration Date
  • Pros: 那些错误证书最终会过期
  • Cons: 要 renew，麻烦
• Announcing Revoked Certificate: 维护一个无效证书列表
  • Cons: 列表最终会非常长，并且用户必须实时更新(否则就无法得知最新的被无效化的证书)

Password Hashing

在存用户密码的时候，只是单纯对密码加密一下即存储 $H(password)$ 是不太可行的(可以暴力破解)

• 事实上，假设有 $M$ 个可能的密码和 $N$ 个用户，暴力破解可以优化到 $O(M+N)$

如果我们为每一个用户设置一个(可以公开的) $salt$ ，存储 $H(password || salt)$，暴力破解就只能 $O(MN)$

我们也可以采取增大常数的方法: 采用一个更慢的 Hash 函数

对密码的攻击可以分为以下两种:

• Offline attack: 比如 Mallory 偷了整个密码文档然后自己在本地暴力 Hash，可以并行

• Online attack: 和服务器交互，不能并行

  • 可以通过加时限或者加数量限制来防御

Merkle Tree

Consider a database that we want to guarantee integrity on to a third party, without revealing more than absolutely necessary

我们想要证明 row #x 确实在 database 中，但是

• 每次只能发送少量信息
• 在更新数据库的时候不用重复计算太多次
• 不要泄漏额外信息

有几个很 naive 的想法:

1. 发送 $(row,H(row))$ : 不行，因为 Hash 函数是公开的
2. 发送$(row,\text{HMAC}(K,row))$: 这下别人不能伪造了，但我们自己还是可以(因为 Key 就是我们自己创建的)

我们可以用下面的树状结构!!!!! (Merkle Tree)

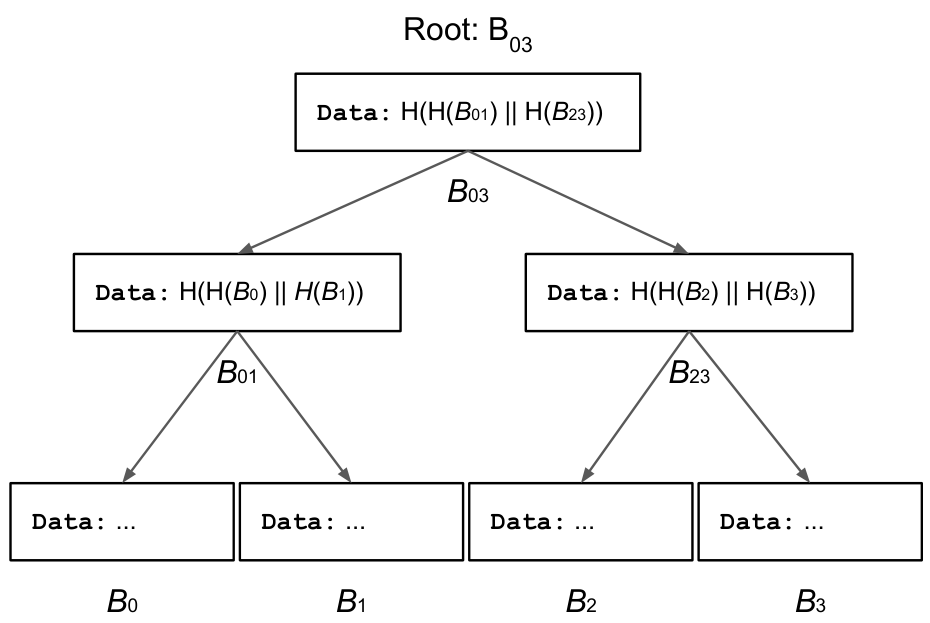
发送信息 $B$ 的时候，发送 $B$ 本身以及到根节点路径上所有兄弟节点的 Hash 值

• 比如发送 $B_0$ 时就需要发送 $B_0, H(B_1),H(B_{23})$

验证的时候逐级向上验证，最终和根节点比对

• 上述例子，在验证时依次计算 $B_{01}$ 和 $B_{03}$，然后 check $B_{03}$ 是否吻合

这样第三方只要 trust root 就可以 trust all

更新的代价显然是对数级别的

HW3 3.6第4问 4.2

6.10 应该是n-1 9

HW4 1.5 2.3 4.4 5.2 6.2 8.1 8.4 9.1