量子计算机编程 从入门到实践

106287780_p11

Programming Quantum Computers —— Essential Algorithms and Code Samples

QPU编程入门

QCEngine实验网址

QPU指令集

以下是一个汇总

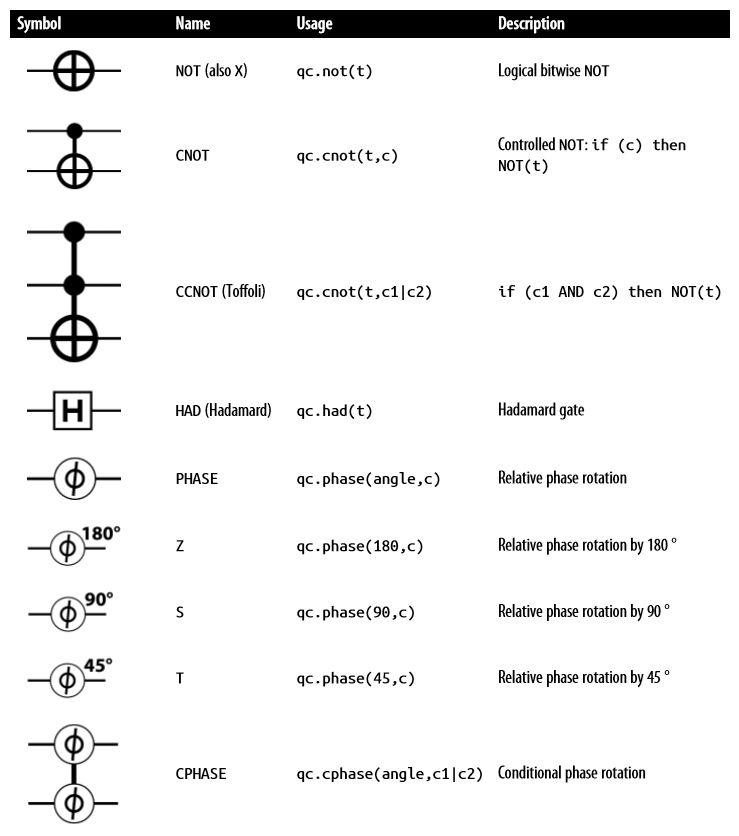
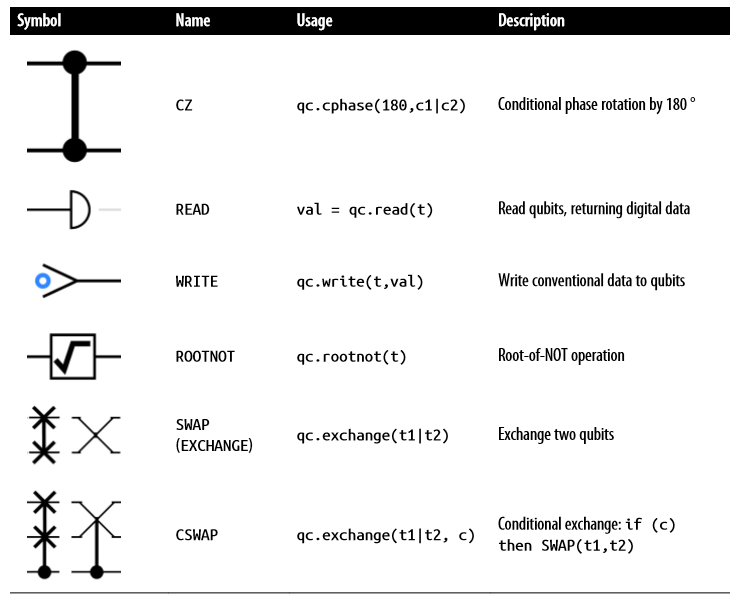
QPU-instruction

QPU-instruction

下面介绍几个比较难的(尤其是经典电路里面没有的门)

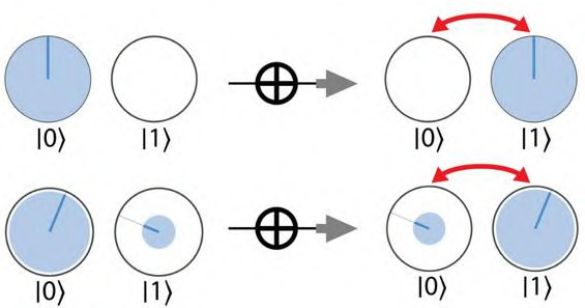
NOT

简单地调换 0 和 1
image-20230526000700265

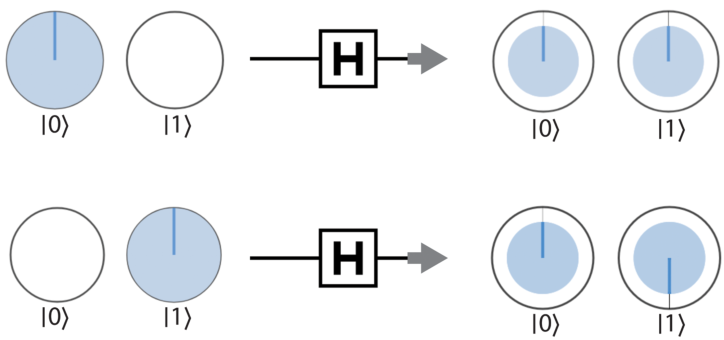
HAD

Hadamard 门的作用是:

\[H(\alpha|0\rangle+\beta|1\rangle)=\frac{\alpha+\beta}{\sqrt{2}}|0\rangle+\frac{\alpha-\beta}{\sqrt{2}}|1\rangle \]

对 \(|1\rangle\) 态应用 HAD，会在一个圆中产生非零旋转(相对相位)
所以可以使用 HAD 门来产生一个随机数(因为进入了叠加态)
注意这个操作的逆操作就是自身
image-20230526010107749

PHASE

注意只有 \(|1\rangle\) 态才会被旋转(因为只关心相对相位)
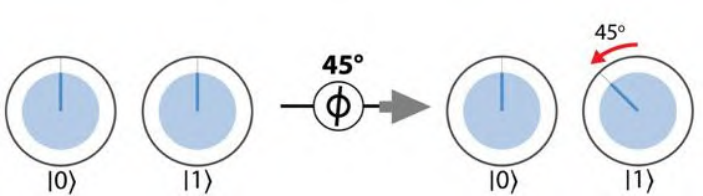
image-20230526001334171

img
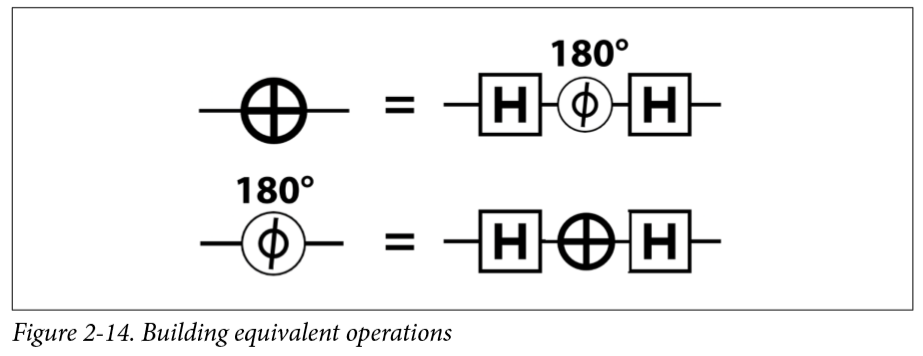
这里可以构造出几个等效操作，可以实验验证一下

qc.reset(1);         // allocate one qubit
qc.write(1);         // write the value zero
qc.had();            // place it into superposition of 0 and 1
qc.not();
qc.had();
var result = qc.read();  // read the result as a digital bit

RNOT

Root of NOT，这个指令经典电路里面没有，两个 RNOT 门连在一起一个 NOT 门
一个简单的实现如下

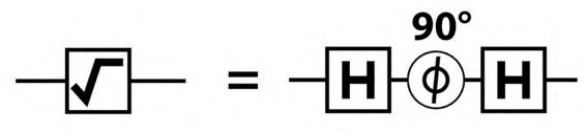
image-20230526002356101

注意到 HAD 门的逆操作是自身，所以由之前的等效电路可以证明出来(感觉有点像矩阵对角化那个，之后学了这里面的数学表述再来看看)

实践: 量子监听测试

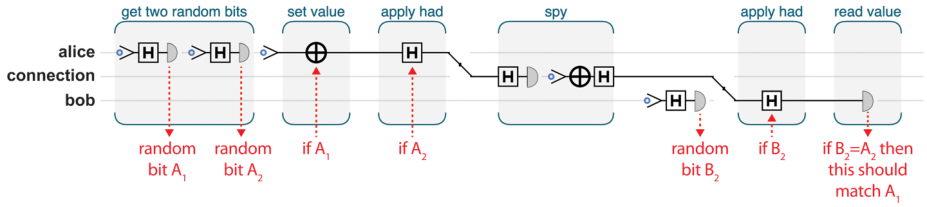
image-20230526005535721
原理在于可以通过 HAD 门抵消自身，但是监听者并不知道有没有使用，所以会导致结果不一致
代码中的 spy 猜测使用了 HAD 门并发出去，正确率为 50%(?)，采用多个量子比特传输可以使得概率极小

qc.reset(3);
qc.discard();
var a = qint.new(1, 'alice');
var fiber = qint.new(1, 'fiber');
var b = qint.new(1, 'bob');

function random_bit(q) {
    q.write(0);
    q.had();
    return q.read();
}
// Generate two random bits
var send_had = random_bit(a);
var send_val = random_bit(a);
// Prepare Alice's qubit
a.write(0);
if (send_val) // Use a random bit to set the value
    a.not();
if (send_had) // Use a random bit to apply HAD or not
    a.had();
// Send the qubit!
fiber.exchange(a);
// Activate the spy
var spy_is_present = true;
if (spy_is_present) {
    var spy_had = 0;
    if (spy_had)
        fiber.had();
    var stolen_data = fiber.read();
    fiber.write(stolen_data);
    if (spy_had)
        fiber.had();
}

// Receive the qubit!
var recv_had = random_bit(b);
fiber.exchange(b);
if (recv_had)
    b.had();
var recv_val = b.read();

// Now Alice emails Bob to tell
// him her choice of operations and value.
// If the choice matches and the
// value does not, there's a spy!
if (send_had == recv_had)
    if (send_val != recv_val)
        qc.print('Caught a spy!\n');

多个量子比特的状态表示

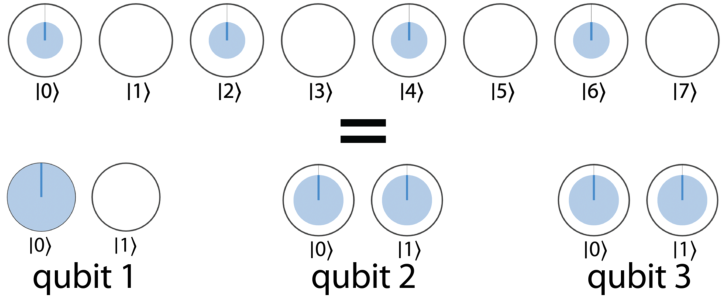
image-20230526012635544

注意看，qubit 1 的\(|0\rangle\)其实就是 0，2，4，6 位 \(|0\rangle\)的和，其他类似，可以通过这种方法把多量子转化回几个单量子

qc.reset(3);
qc.write(0);
var qubit1 = qint.new(1, 'qubit 1');
var qubit2 = qint.new(1, 'qubit 2');
var qubit3 = qint.new(1, 'qubit 3');
qubit2.had();
qubit3.had();

在使用 qc.reset() 在寄存器中设置一些量子比特后，使用 qint.new() 将它们分配给 qint 对象。qint.new() 的第 1 个参数指定了要从 qc.reset() 创建的栈中拿多少个量子比特分配给这个 qint 对象。第 2 个参数是在量子电路可视化工具中要使用的标签。

多量子比特运算

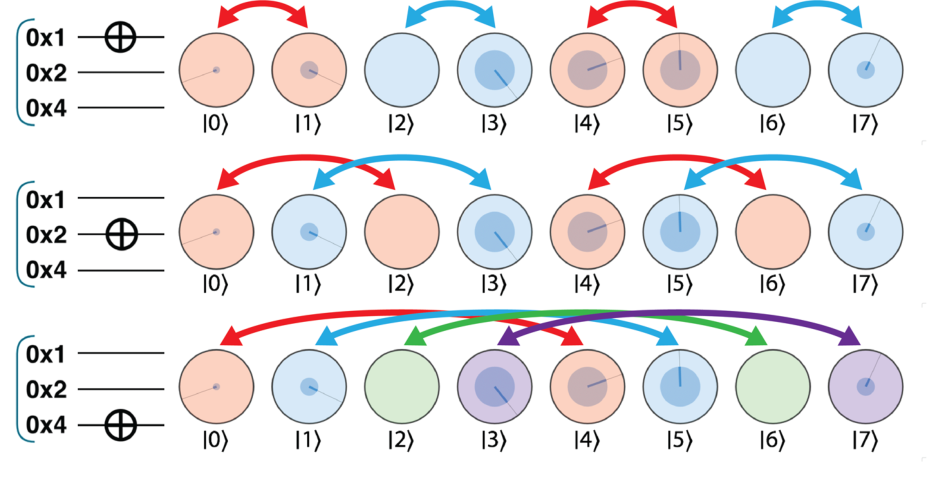
image-20230526162635711

多量子比特运算对算子对(operator pair)进行运算，比如如果对 0x4 进行运算，那么每个算子对会包括差正好为 4 的那些圆

PHASE

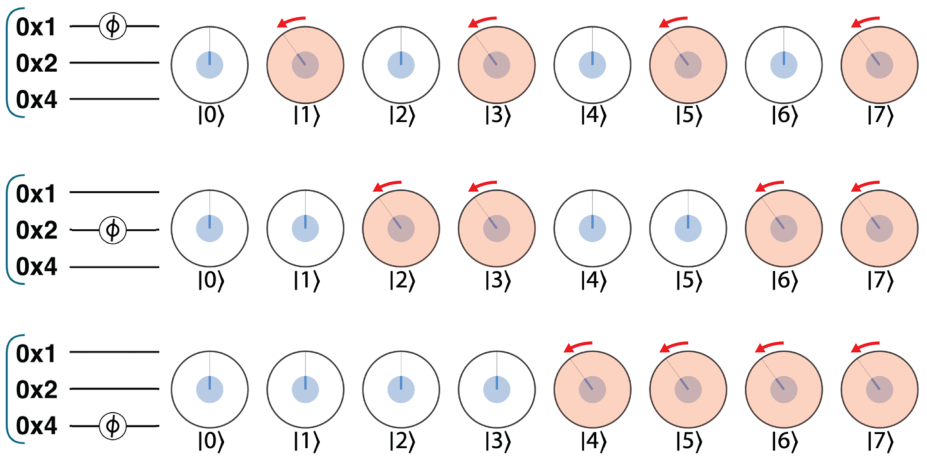
image-20230526163117986
旋转算子对中右边的圆

READ

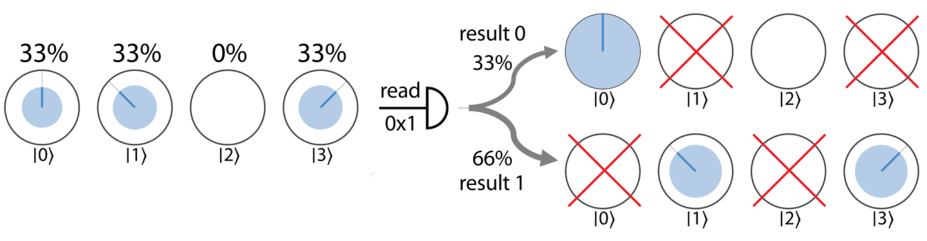
image-20230526163210951
注意与结果不一致的圆概率会被清零，剩下的概率会重新按比例分配

CNOT和CCNOT

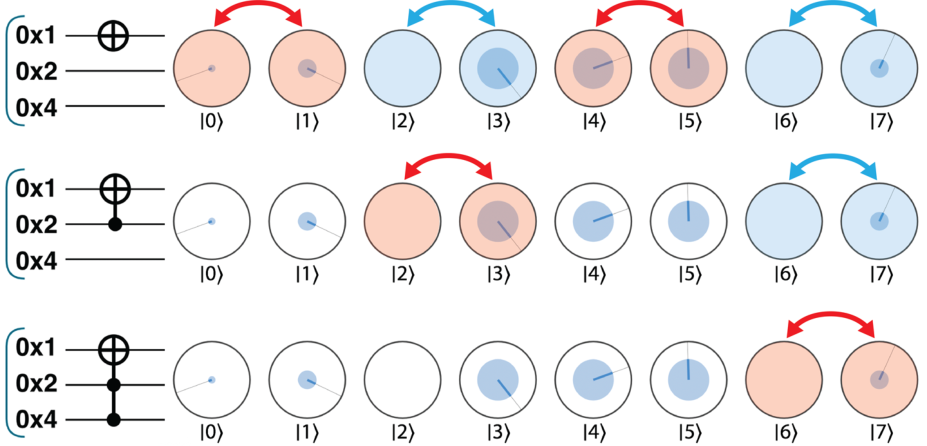
image-20230526172350969
这是条件指令，只有当条件量子比特为 1 时才会执行，否则不执行，结合图很好理解
(其实就是固定几个二进制位进行 NOT 操作，所以仍然保持 NOT 的可逆性，自身即为逆运算)

CPHASE

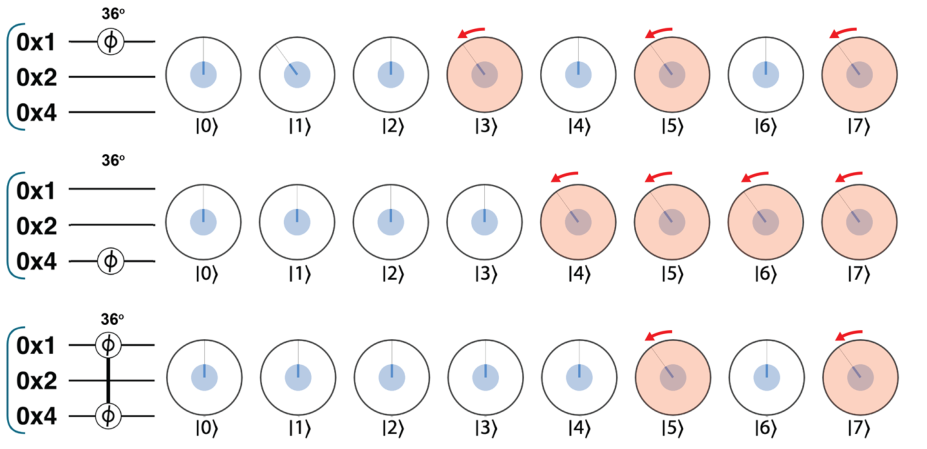
image-20230526164634129
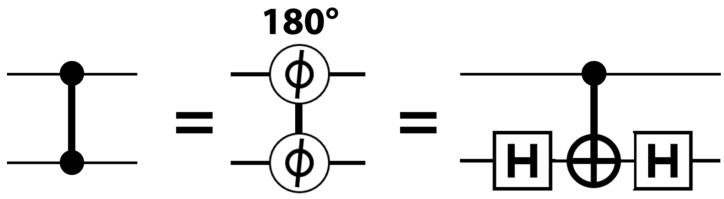
同样是控制二进制位，和 PHASE 类似也有等价表示方法

image-20230526164721852

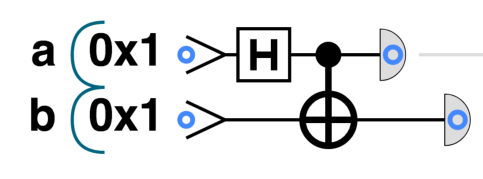
实践: 贝尔对(Bell Pairs)

这里的两个量子比特在读取时永远一致(从电路图可以看出这是显然的)，这实际上是一种量子纠缠
image-20230526164330544

实践: 相位反冲(Phase Kickback)

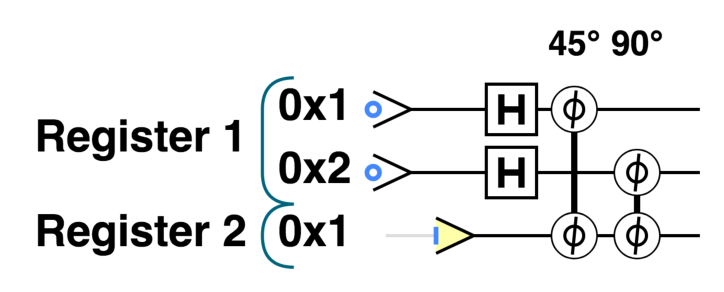
image-20230526171847132

注意 Register2 一直保持\(|1\rangle\)的状态，可以说他没有变化(事实上 Register2 根本没有进入叠加态)

qc.reset(3);
// Create two registers
var reg1 = qint.new(2, 'Register 1');
var reg2 = qint.new(1, 'Register 2');
reg1.write(0);
reg2.write(1);
// Place the first register in superposition
reg1.had();
// Perform phase rotations on second register,
//conditioned on qubits from the first
qc.phase(45, 0x4, 0x1);
qc.phase(90, 0x4, 0x2);

利用相位反冲可以构造更通用的条件运算

实践: 交换测试(Swap Test)

这个测试可以用来检测两个量子比特是否相同，如果相同，那么最后的结果为 1，否则为 0

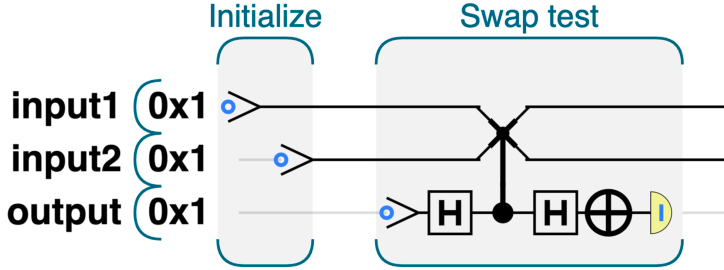
image-20230527003209262

注意原理，这里只会交换 5 和 6 对应的圆，而如果原来是 0 或者 3 状态，经过 output 位上的 HAD 门之后不会有概率被分配到 5 和 6 对应的圆上，相当于一个空操作，反之会进入叠加态导致有概率出错

实践: 量子隐形传态(Quantum teleportation)

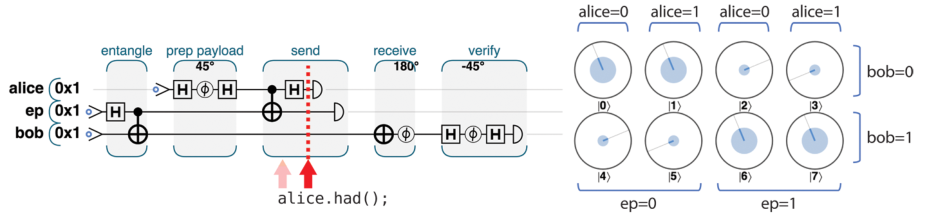
image-20230527103035968

如图，receive 环节中也可以采用 CNOT 和 CZ 来实现(注意这里 alice 和 ep 都变成了传统比特)，对右图的解释如下

• In the first column (where alice=0 and ep=0), we have Alice’s payload, exactly as she prepared it.
• In the second column, we have the same thing, except with a PHASE(180) applied.
• In the third column, we see the correct payload, but with a NOT having been applied to it (∣0⟩ and ∣1⟩ are flipped).
• Finally, the last column is both phase-shifted and flipped (i.e., a PHASE(180) followed by a NOT).

量子算数与逻辑

  • Moving and copying data: 我们不能使用赋值运算(不支持)，因为我们不能移动或者复制量子比特
  • Reversibility and data loss: 除了 READ 操作，其他都是可逆的(尽量不要用不可逆操作，否则我们为什么不使用传统计算机？)

量子算术运算

下面是几个比较简单的量子整数运算(其实和传统电路差不多，只不过可以对叠加态操作)

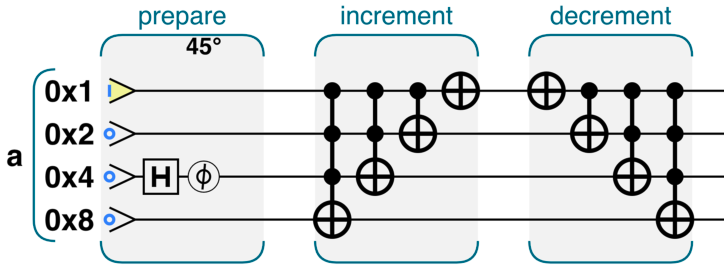
image-20230531103927788

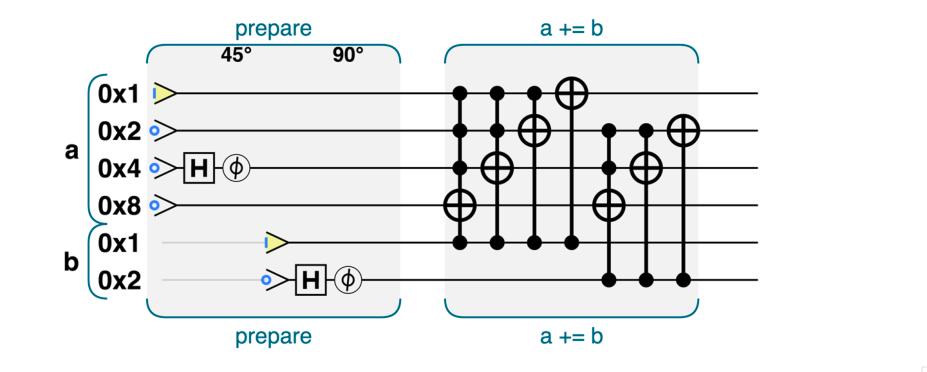
image-20230531104132395

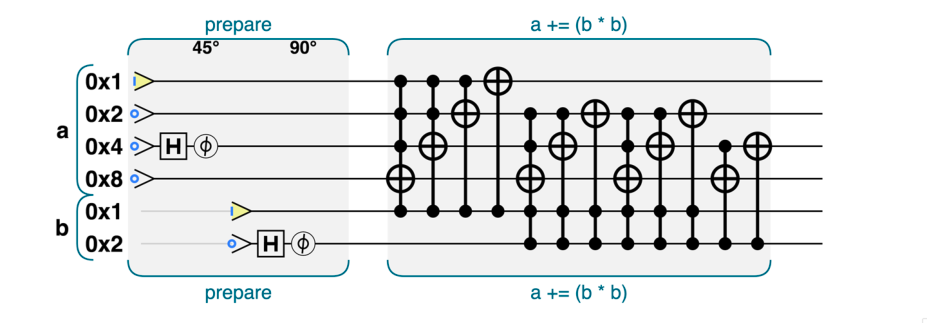
image-20230531104219907

量子条件执行

image-20230531105251890

一个重要应用: 相位编码，它可以帮助我们找到不被读操作破坏的答案(因为完成运算的时候寄存器强度保持不变，读出每个值的概率保持不变)

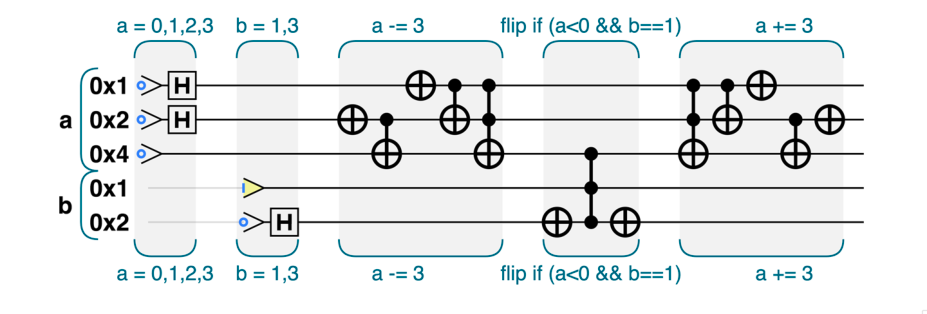
image-20230531110810479

可逆性和临时量子比特

很多运算没有可逆性(Reversibility)，比如绝对值运算，因为丢失了信息。那么我们如果想要用量子方法实现就必须把丢失的信息保存起来，这样才能保证可逆性，用于保存丢失的信息的单元就是临时量子比特(Scratch Qubits)

以绝对值运算为例，用圆形表示法的观点来理解就是将后面四个圆移动到了第二行，然后操作

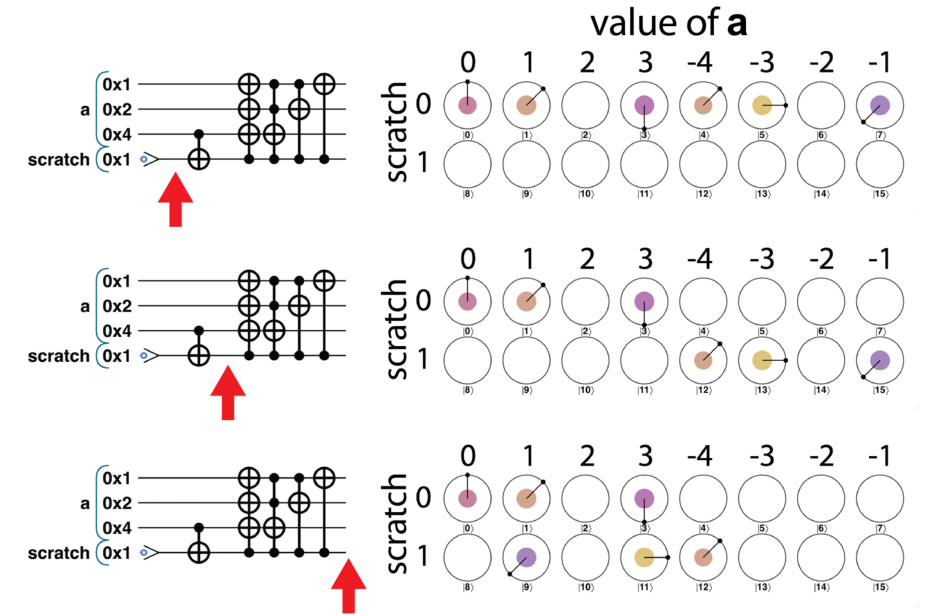
image-20230531113204756

反计算(Uncomputing)

在使用临时量子比特的时候，临时量子比特会和 QPU 寄存器纠缠在一起，如果我们要进行别的不可逆计算就必须要新的量子比特(因为强制清零会影响到 QPU 寄存器)，所幸我们有一个技巧解决这个问题，就是反计算(Uncomputing)

一旦运用这个技巧，我们的 QPU 也将退回计算前的初始状态(并且不能在此之前复制或者移动)，但是一般情况下我们会将结果在反计算之前传输出去(因为别的计算需要这个结果)，反之我们可以就直接读取

In quantum computation, this trick is extremely common: use temporary scratch qubits to perform an otherwise-irreversible computation, perform other operations conditional on the result, and then uncompute.

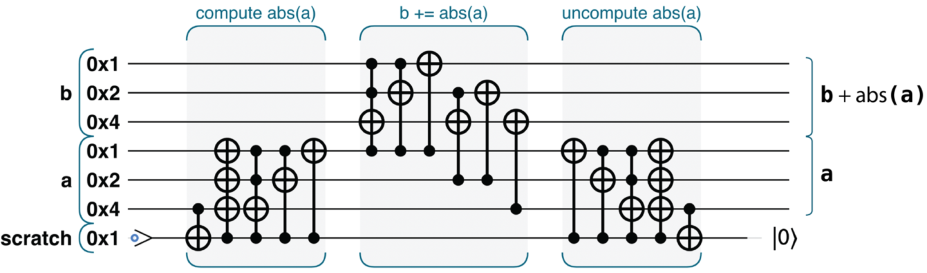
image-20230531114126820

反计算的另一个十分常见的应用涉及执行某个运算（可能会用到临时量子比特），将结果存储在输出寄存器的相对相位中，然后对结果进行反计算操作。只要初始运算和最后的反计算步骤不干扰输出寄存器的相对相位，相位信息就可以在整个过程中完好无损。

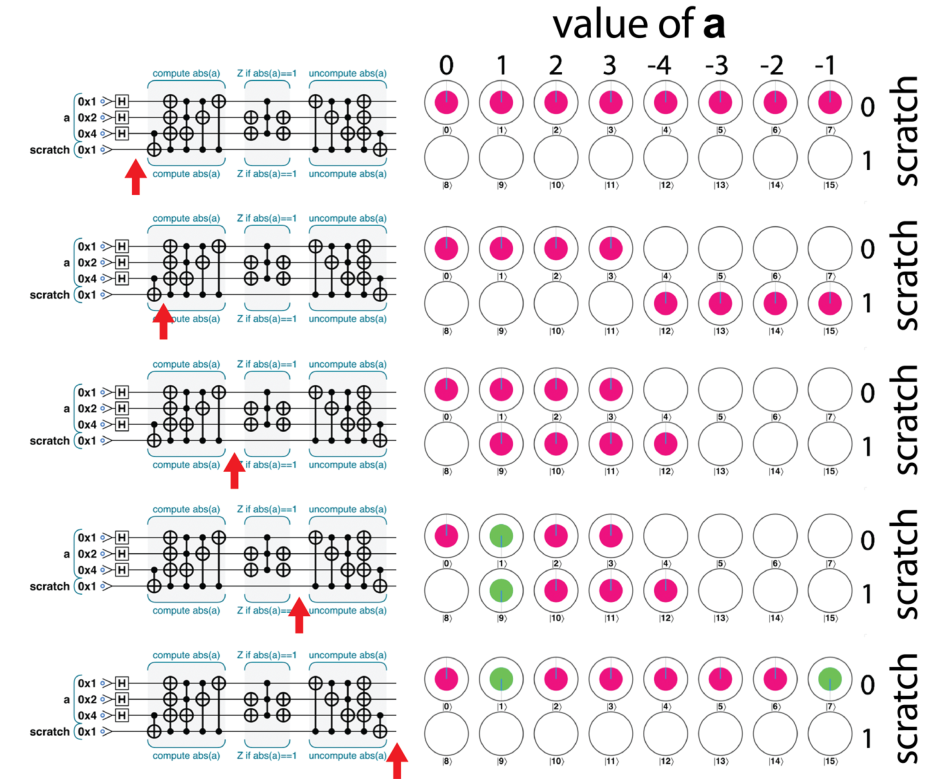
image-20230531115534834

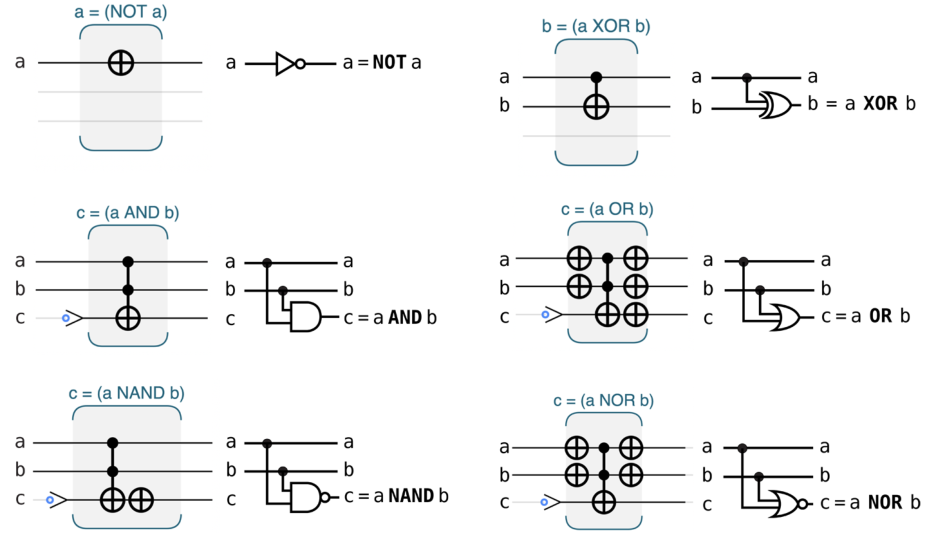
量子逻辑运算

与传统逻辑类似，但是需要使用临时量子比特维持可逆性，以下是用 CNOT 门构建的传统逻辑组件

image-20230531120137274

振幅放大

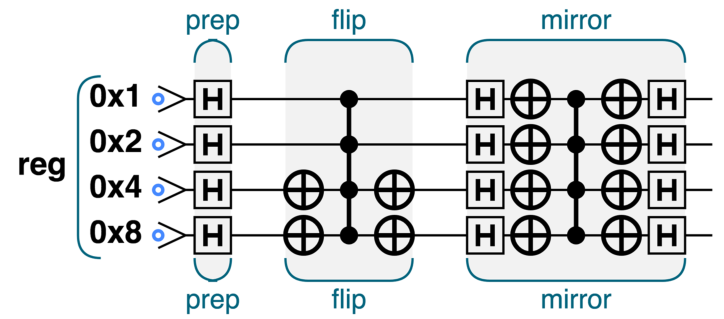
image-20230531124727561

注意翻转操作，通过圆形表示法很好理解，中间的步骤就是翻转第 15 位，两边的 NOT 门负责转换到第 3 位，由此我们也可以得到翻转的一般电路(此处略去，就是需要翻转的位置如果二进制表示的某一位为 0，那么就需要一个 NOT 门，如果是 1 就不需要)

对于镜像操作，可以把相位差转化为强度差，这样我们就可以读出变化(这非常重要)，注意镜像操作在量子计算文献当中通常被称为格罗弗迭代

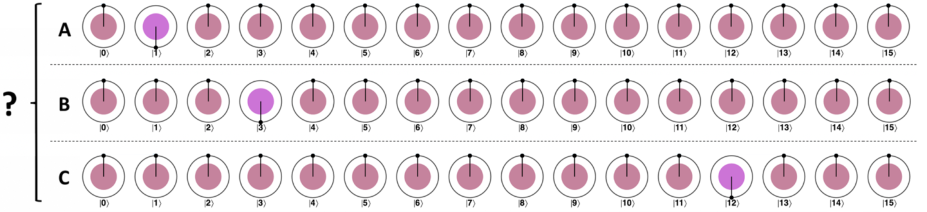
image-20230531125151614

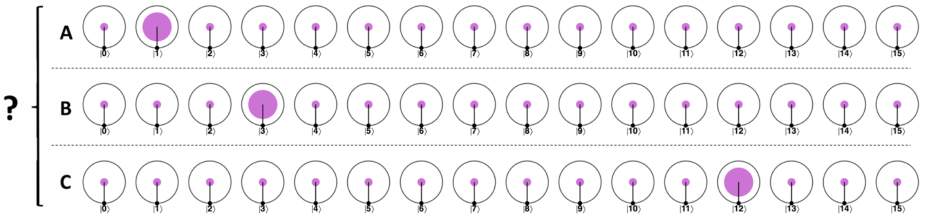
image-20230531125206266

镜像操作的理解

从圆形表示法来看，镜像子例程执行以下步骤

  1. 求所有值（圆）的平均值。这可以通过对圆内各点的 \(x\) 值和 \(y\) 值进行数值平均来实现。在计算平均值时，应将零值（空心圆）作为 [0.000, 0.000] 包含在内

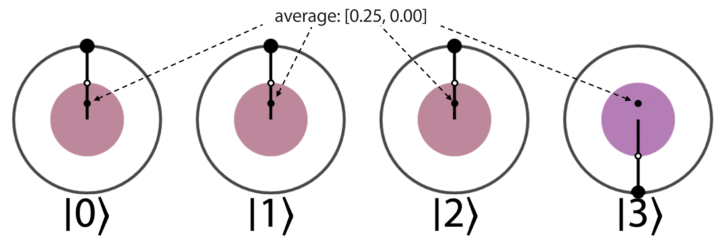
    image-20230531154247737

  2. 根据平均值进行翻转

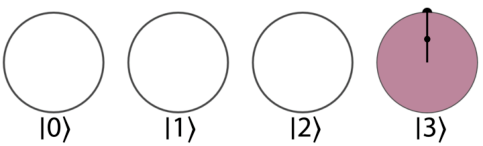
    image-20230531154258179

因为大多数值是相同的，所以平均值接近大多数值，而远离具有相反相位的值。这意味着，当根据平均值翻转时，具有不同相位的值会像“弹弓”一样，弹射到平均值的另一侧，并从其他值中脱颖而出

AA 迭代

组合以上两个操作即可，代码如下，这个组合被称作振幅放大迭代(amplitude amplification iteration)简称 AA 迭代

var number_to_flip = 3; // The 'marked' value
var num_qubits = 4;
qc.reset(num_qubits);
var reg = qint.new(num_qubits, 'reg')
reg.write(0);
reg.hadamard();

// Flip the marked value
reg.not(~number_to_flip);
reg.cphase(180);
reg.not(~number_to_flip);

reg.Grover();

但并不是迭代次数越多越好

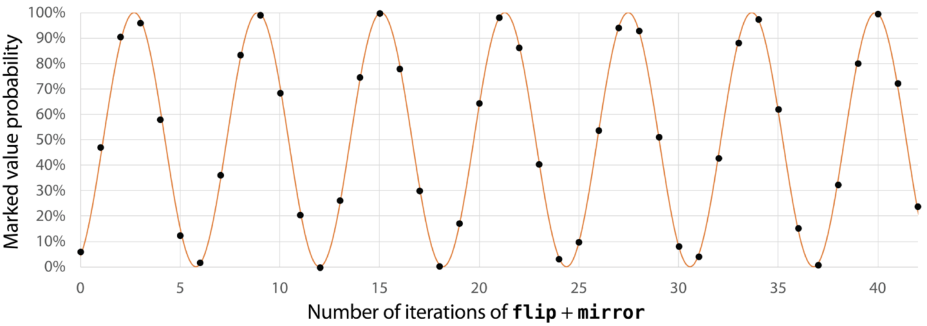
image-20230531144019509

一般来说，设量子比特数为 \(n\) ，则最佳迭代次数为:

\[N_AA = \lfloor\dfrac{\pi\sqrt{2^n}}{4} \rfloor \]

多个标记值的情况类似，只是曲线的周期变小，设 \(m\) 为标记值的数量，则最佳迭代次数为:

\[N_AA = \lfloor\dfrac{\pi}{4} \sqrt{\dfrac{2^n}{m}}\rfloor \]

量子傅里叶变换

振幅放大不能区分出下面几个状态(注意它们都是正弦波)

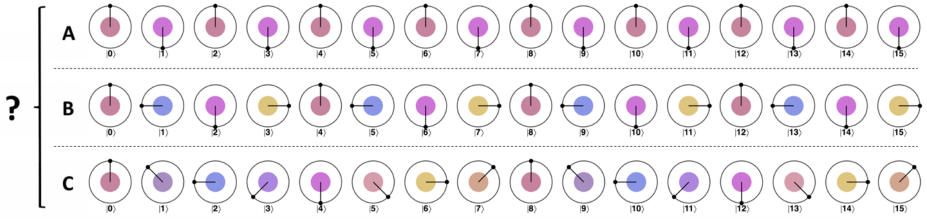
image-20230601100520929

但是量子傅里叶变换 (QFT) 可以，按照周期的不同，上面几个状态分别被变换为

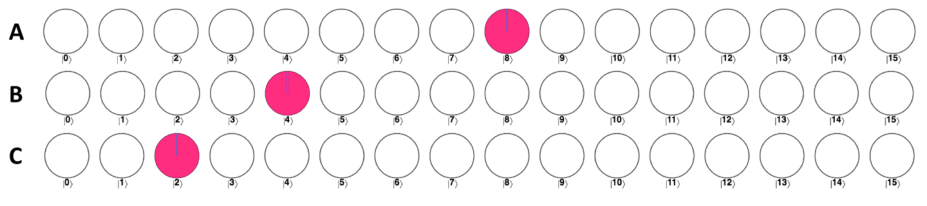
image-20230601100637615

电路图如下(原理先不要深究，当成一个黑箱，后面再解释)

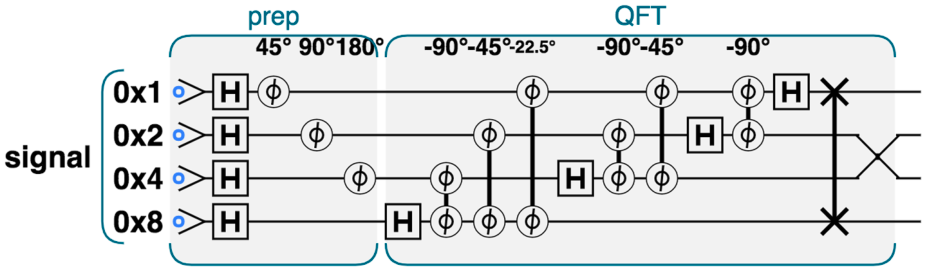
image-20230601113436802

离散傅里叶变换 (DFT)

The DFT acts on discrete samples taken from a signal, whether it be a musical waveform or a digital representation of an image. Although conventional signals are normally thought of as lists of more tangible real values, the DFT will also work on complex signal values. This is especially reassuring for us, since (although we try our best to avoid it) the full representation the state of a QPU register is most generally described by a list of complex numbers.

DFT 将信号转换成频率空间 (frequency space)，对于实数输入信号而言会有下图所示的对称效应(复数输入信号没有)

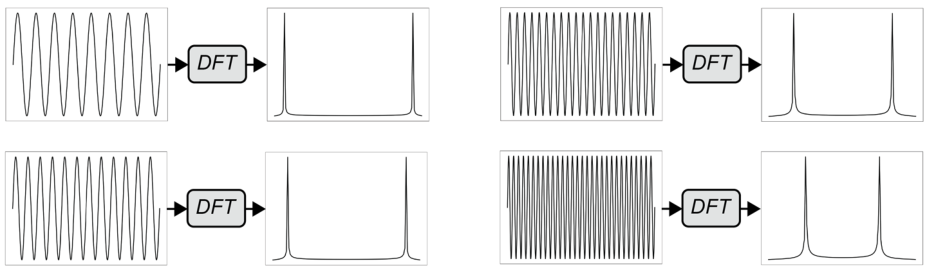
image-20230601114421593

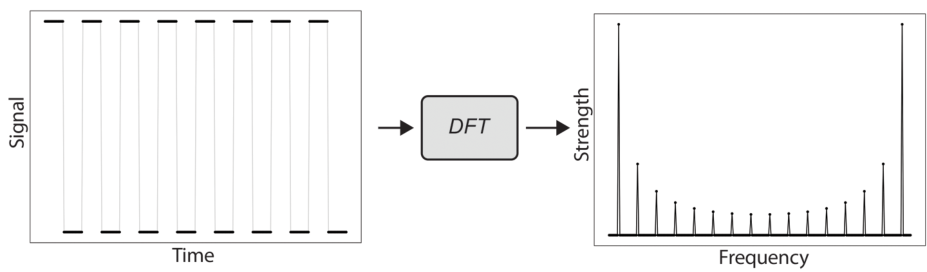
对方波信号应用 DFT 的结果如下

image-20230601114708978

QFT

对于正弦波的 QFT 已经在上面展示过了，下面展示方波的 QFT

image-20230601192048927

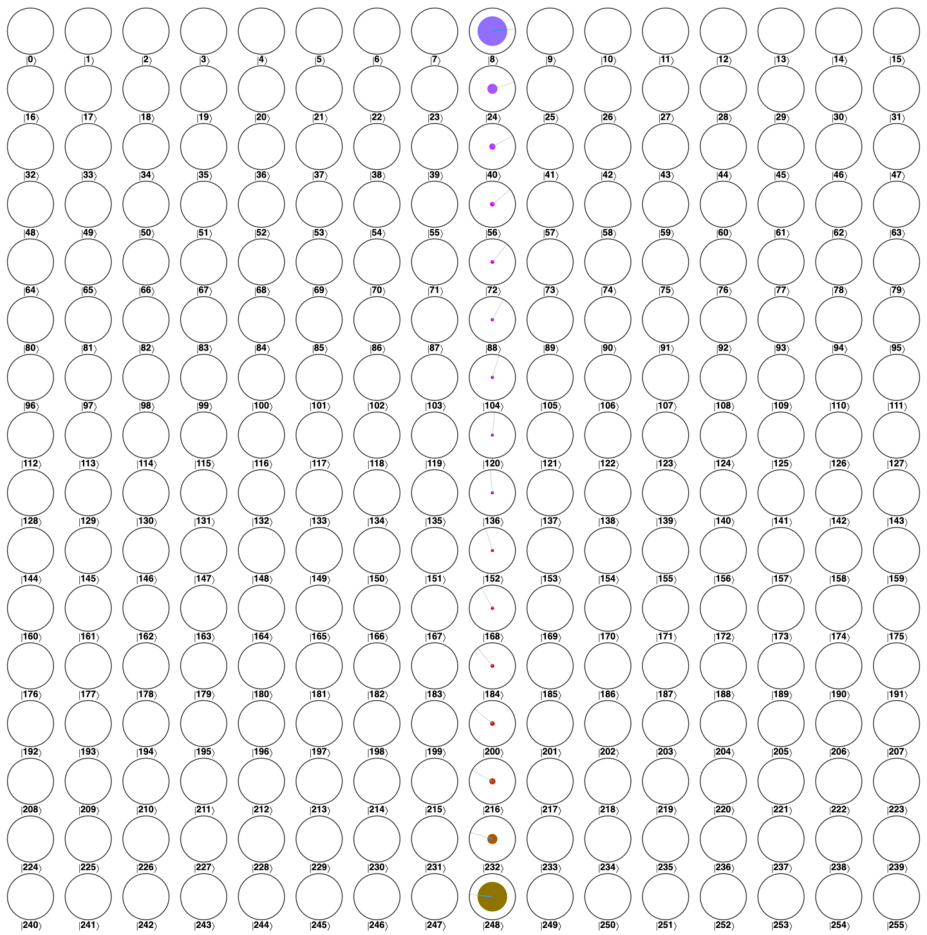
image-20230601192058771

可见频率空间中的每个分量都被编码在 QPU 寄存器状态的强度和相对相位中。这意味着针对应用 QFT 后的寄存器读出给定频率的概率取决于给定频率对信号的贡献程度。

invQFT

在量子计算里面大部分操作都可逆， QFT 也不例外，我们可以使用 invQFT 操作将频率空间的信号转换回去，从而制备周期性变化的寄存器叠加态，通常比用电路来制备容易

  • 周期性相位变化( from 一个实数纯态)

    image-20230601201119011

  • 周期性强度变化( from 一个对称实数信号)

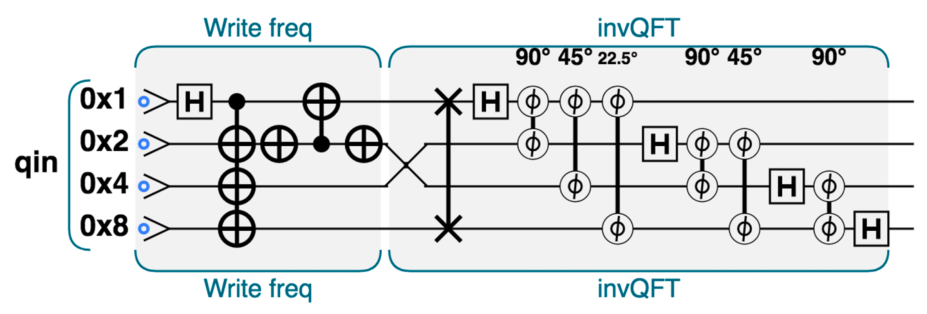
    image-20230601201244419

有了 invQFT， 我们可以就可以修改频率(先用 QFT 转换到频率空间进行操作，比如加法，然后再用 invQFT 转换回来)

image-20230601201656330

内部原理

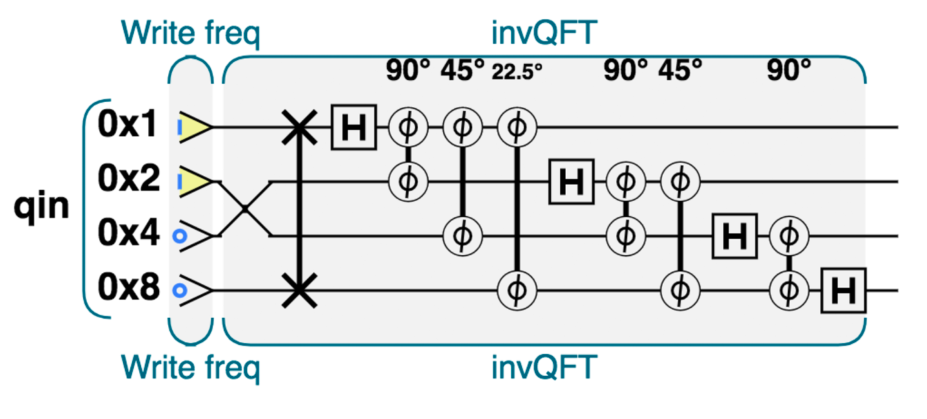
由于运算的互逆性，我们弄懂 invQFT 就行，先来看一个很容易理解的产生相位编码的电路(原理就是二进制拆分)

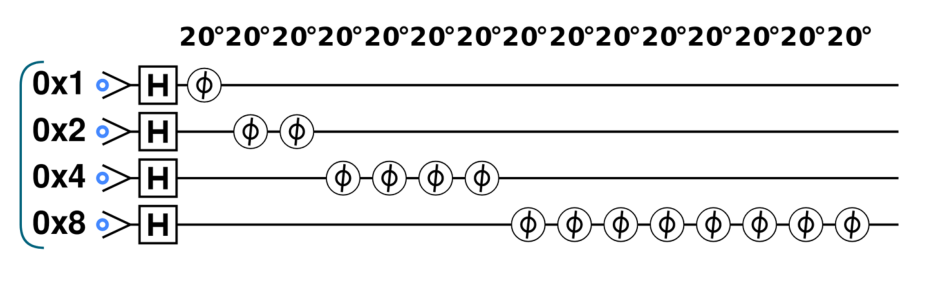
image-20230601225547306

之后的没太懂，之后再来补

Shor 分解算法

这个与 RSA 公钥加密有关，有关的内容读者可以自行查询，此处不做赘述

我们实际上是要求满足 \(x^r\equiv 1\pmod N\) 的最小的 \(r\) (其中 \(n\) 和 \(x\) 互质)，这可以转化成一个求周期的问题，先看个例子

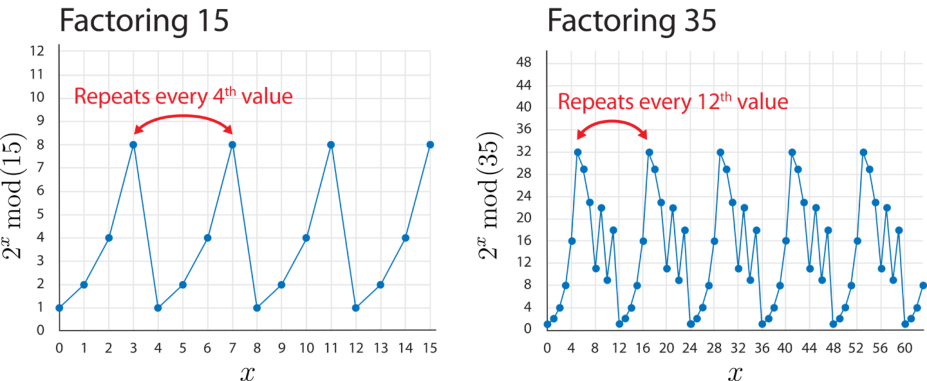
image-20230604102453888

原理

从一些群论的知识我们可以推出，如果 \(n\) 和 \(x\) 互质，那么这个同余类就是 \([1, n-1]\) 的所有整数，一共有 \(n-1\) 个数，必然存在周期性，上限即为 \(n-1\) ，一旦哦我们确定了这个周期，倘若 \(r\) 是偶数，那么我们可以得到

\[(x^{\frac{r}{2}}-1)(x^{\frac{r}{2}}+1)\equiv 0\pmod N \]

由于\(r\)是最小的周期，所以 \(x^{\frac{r}{2}}-1 \not \equiv 0 \pmod N\) ，如果此时 \(x^{\frac{r}{2}}+1 \not \equiv 0 \pmod N\) 的话，我们就有两个都不能被 \(n\) 整除的数，而它们的乘积却能被 \(n\) 整除，所以 \(gcd(x^{\frac{r}{2}}-1,n)\) 和 \(gcd(x^{\frac{r}{2}}+1,n)\) 之中至少有一个是 \(n\) 的非平凡因子，这样我们就可以分解 \(n\) 了

实例

先制备叠加态然后在该进行乘法的地方进行乘法
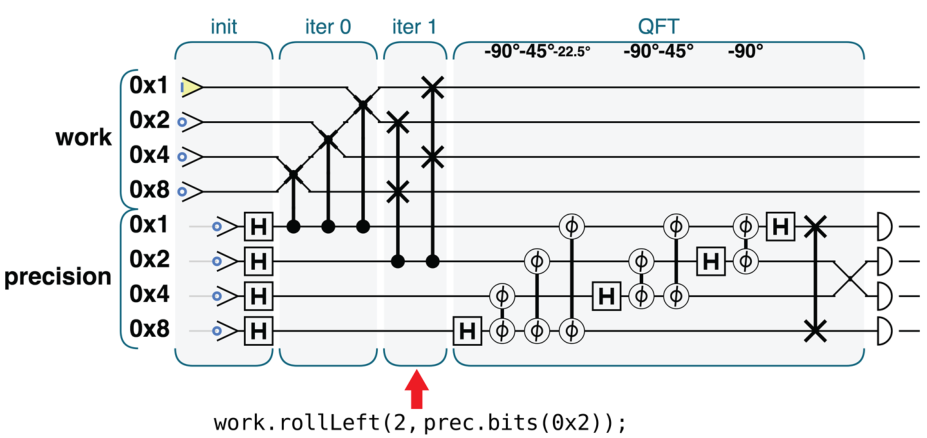
image-20230604171450669

可以看出已经有了循环的样式
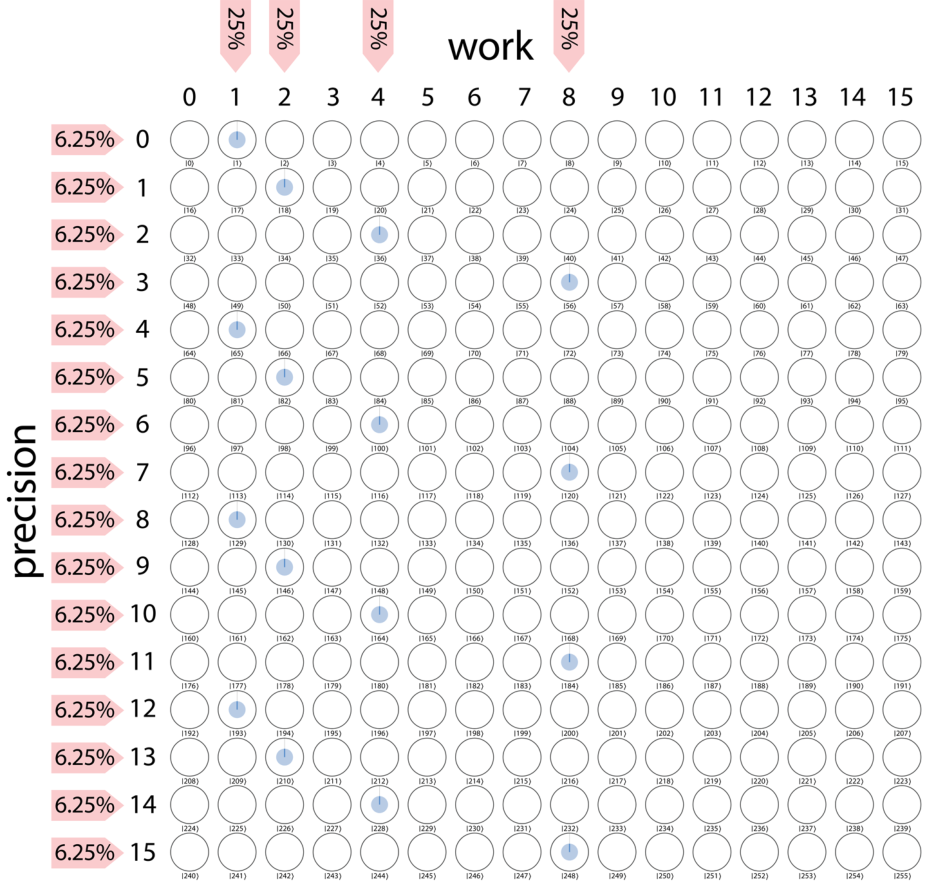
image-20230604171630631

进行一个 QFT 之后变成了这样

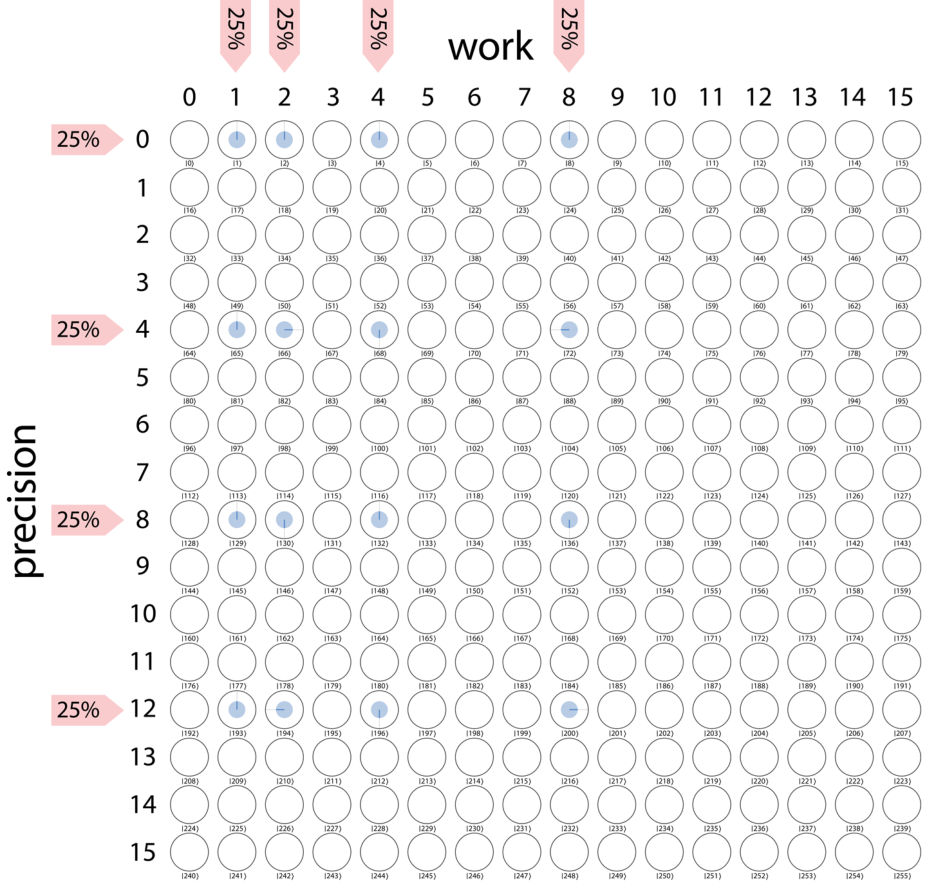
image-20230604172012814

之后进行读取就可以了

posted @ 2023-05-21 10:20  520Enterprise  阅读(405)  评论(0)  编辑  收藏  举报