kmeans算法代码实现

import matplotlib.pyplot as plt #画图用
import random
import copy
import operator #判断列表相等
k=2 #簇数量
data=[(1,2),(2,3),(2,4),(3,3),(10,16)]
def show(x):
    for j in x:
        plt.scatter([i[0] for i in j],[i[1] for i in j])#取第一列元素
   #plt.show()
    plt.savefig('zz.png')

# 1，随机选定K个值作为初始聚类中心
def chushi():
    core=[]
    data3=copy.deepcopy(data) #避免出现修改原数据的情况
    for i in range(k):
        el=random.choice(data3)
        data3.remove(el)#排除重复元素
        core.append(el)
    print("初始核心为",core)
   # print("数组为",data)
    return core
# 2，求每个样本与K个聚中心的距离，取最近的中心，作为该样本的标记中心
def setcu():
    p = [[] for j in range(k)]
    return p
def getjuli(x):
    p=setcu()

    for i in data:
        num = 0  # 数组号
        num1= 0
        juli = 1000  # 距离
        for j in x:

            len=pow(pow(i[0]-j[0],2)+pow(i[1]-j[1],2),0.5)
            len=round(len,2)
            print(len)
            num = num + 1
            if(len<juli):
                juli=len
                num1=num
        print("分组为",num1-1)
        p[num1-1].append(i)
    return p


# 3，求各个聚类簇的均值，得出k个新的中心点
def leijia(x):
    num=0
    x1=0
    y1=0
    re=[]
    if(x!=[]):
        for i in x:
            num=num+1
            x1=x1+i[0]
            y1=y1+i[1]
        x1=x1/num
        x1=round(x1,2)
        y1=y1/num
        y1=round(y1, 2)
        re.append(x1)
        re.append(y1)
        return re
    else:
        return []
# 如果与旧中心点一样，结束聚类过程

# 如果与旧中心点不一样，将新的中心点作为聚类中心重复第二步
#
# 确定K中心点个数的方法：1，经验法
#
# 2，手肘法，通过观察中心点K数量和簇内误方差SSE相关曲线，找到最低的一个点就是最佳的K值

if __name__ == '__main__':
    core=chushi();
    p=getjuli(core)
    print("第一组有",p[0])
    print("第二组有",p[1])
    print("聚类一次后，第一组核心",leijia(p[0]))
    print("聚类一次后，第二组核心",leijia(p[1]))
    num=1
    while(1):
        newcore=[]
        newcore.append(leijia(p[0]))
        newcore.append(leijia(p[1]))
        core=newcore
        print("——————————————————第",num,"次分类过程————————————————————————————————")
        num=num+1
        print("新聚类核心为",core)
        p = getjuli(core)
        print("间距为",leijia(p[0]))
        print("间距为",leijia(p[1]))
        print("第一组有", p[0])
        print("第二组有", p[1])
        if(operator.eq(core[0],leijia(p[0]))&operator.eq(core[1],leijia(p[1]))):
            break
    print("最终聚类核心为",core)
    data1=[]
    data1.append(p[0])
    data1.append(p[1])
    print(data1)
    show(data1)

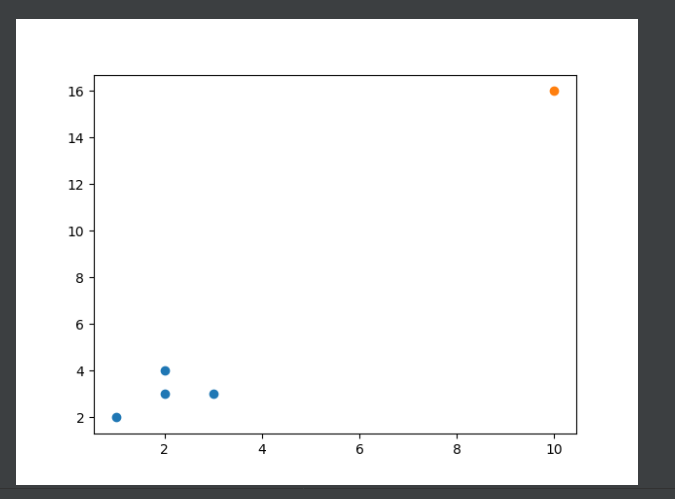
运行结果：

 

 

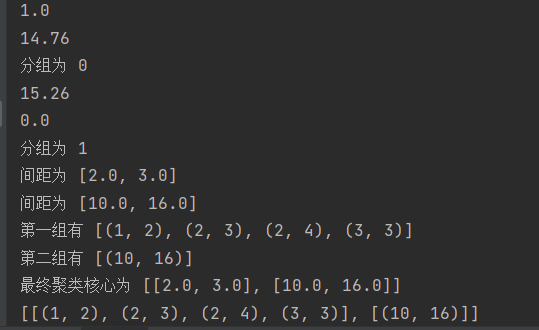
 生成图片为：