多元线性回归
矩阵和向量
矩阵：由数字组成的矩形阵列并写在方括号内
向量是只有一列是矩阵，即nx1的矩阵
Xij表示矩阵元素
Yi表示向量元素
默认从1开始下标，大写表示矩阵小写表示向量
预测=数据矩阵X参数矩阵可以简化计算
矩阵车乘法没有交换律只有结合律
多元线性回归方程
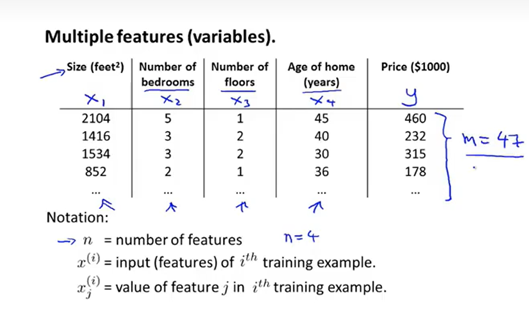
m表示样本数量
n表示特征值数目
xi表示第i个输入样本
xij表示第i个输入样本的第j个参数
线性回归函数假设：
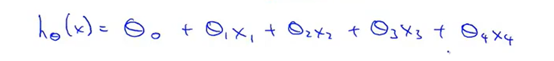
X的特征向量是一个从0开始的n+1维向量
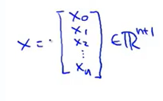
参数向量为
上述回归函数假设可以写成：
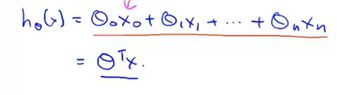
这就是多元线性回归
，代价函数为：
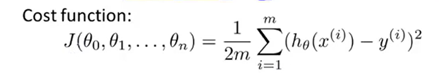
特征值处理
如果在两个影响参数变化范围相差过大的情况下，比如说，影响房价因素，一个是面积变化范围为0-2000英尺，一个是卧室数量，在0-5之间。二者最后会导致，等值线图变得非常的细，扁，这样会导致，梯度下降的过程变得十分艰难，很难得到最优解
因此就需要进行特征值缩放
更容易通过梯度下降得到最优解
除了用参数值除以最大值，还可以通过均值归元化的方式
学习率
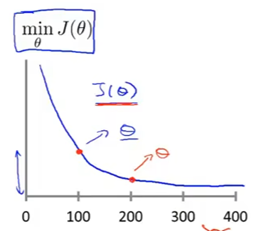
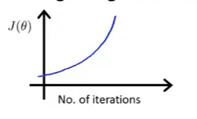
每步迭代后代价函数值和迭代次数之间的关系
如果学习率阿尔法过大就会导致代价函数值变大
从而导致代价函数和迭代次数的函数图像发生变化，就是过拟合
