代价函数以及梯度下降法概述

代价函数

假设训练集是（1,1），（2,2），（3,3）

首先假如给定的拟合函数斜率为不同值，计算在x=1,2,3点处不同的值与实际训练集的值的差的平方，再除以2m(训练集个数)得到的就是代价函数在该斜率点的值

 

 

 

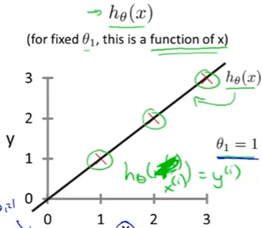
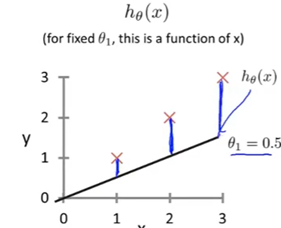
对应的代价函数如下：

 

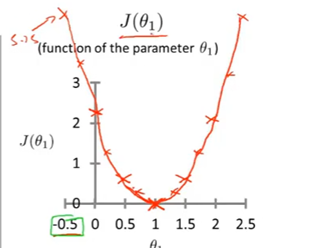
最小值是1，就是目标函数T函数

这是简化的代价函数，线性拟合函数是正比例函数，而非一般的一次函数

 

 

 

 

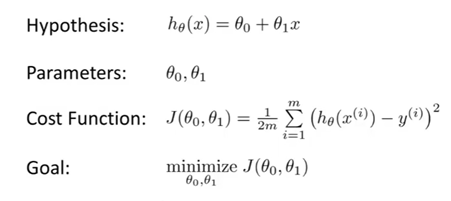
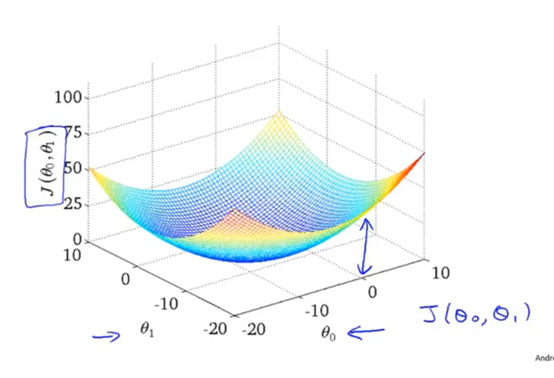
因为拟合函数具有两个参数，所以代价函数的图像如上图

 

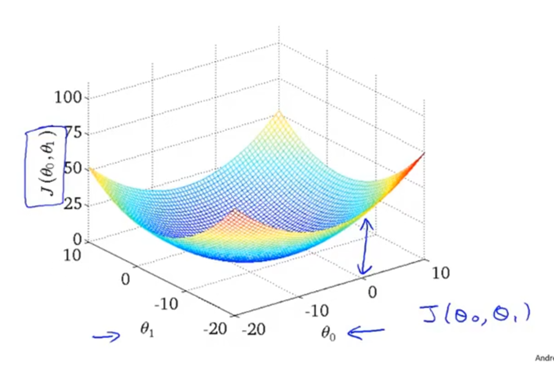
寻找最佳目标函数的方法：

梯度下降

给定初始化的参数值，q0,q1

寻找梯度最小的点，沿着接着最小的点

得到梯度为0点，即为局部最小值点

 

 

 

 

 

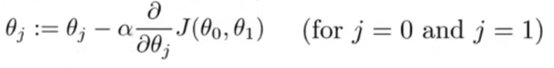
：=表示赋值，赋值运算符

 

赋值更新参数时候要做到同步更新

 

 

 

其中的参数有用到

α是学习率，决定了梯度变化的快慢，即为

 

 

 

在每一点处都对横坐标进行更新，如果其斜率为正就往左移，斜率为负就往右移，最后得到的就是改函数最小值即斜率最低点

 

 

 

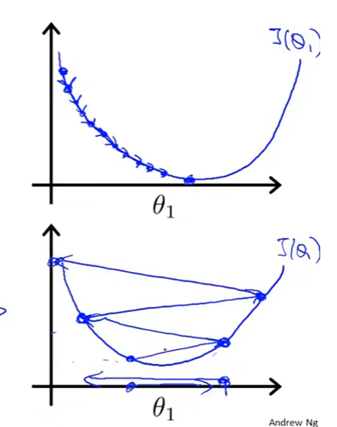
如果α太小，需要很多步才能达到全局最低点

如果α太大，会跨过最低点，最后很难达到最低点

 

 

越靠近最低点，梯度下降会因为斜率变小，自动变慢，直至达到最适合的点，也就是局部最优点

 

线性回归的梯度下降

 

 

 

代价函数带入梯度下降求导数

 

 

 

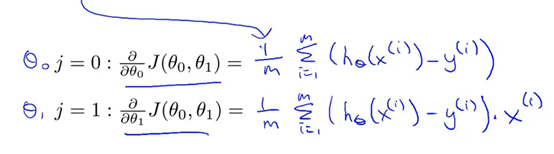
两个参数。求；两次偏导