关于欧拉定理与费尔马定理-费马小定理

关于欧拉定理：看到很多地方包括百科上都是下面方式定义的

如果a,m都属于正整数，且gcd(a,m)=1 ,则会有a^φ(m)≡1(mod m) 

也看到有的数论教材，是设的m是大于1的整数，应下图所示

当然实际上对于这个定理，对于a和m是可以等于1的，甚至都等于1也满足定理

因此只要满足：如果a,m都属于正整数，且gcd(a,m)=1 ,即两个数互质，则会有a^φ(m) ≡ 1 (mod m) 

这里也介绍一下关于欧拉这位杰出的数学家吧

莱昂哈德·欧拉（Leonhard Euler ，1707年4月15日～1783年9月18日），瑞士数学家、自然科学家。
1707年4月15日出生于瑞士的巴塞尔，1783年9月18日于俄国圣彼得堡去世。欧拉出生于牧师家庭，自幼受父亲的影响。13岁时入读巴塞尔大学，15岁大学毕业，16岁获得硕士学位。

 

提到欧拉定理，这里也需要提一下另一个很有名的定理，费马小定理（Fermat's little theorem)

即如果p是一个素数，p不能整除a,也即a不是p的倍数，则会有 a^(p-1) ≡ 1 (mod p）

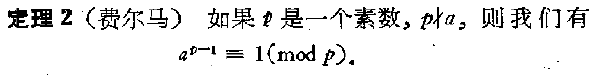
如果先有欧拉定理，费马小定理也非常好推理，因为费尔马定理是欧拉定理的一个特殊情况，但实际上是先有的费马小定理

这里也介绍一下费马这个杰出的数字学吧，关键他还是只是一个业余的数学家，但成就不比职业的数学家差，被誉为"业余数学家之王"

皮埃尔·德·费马(Pierre de Fermat，1601年8月17日～1665年1月12日），法国律师和业余数学家。
他在数学上的成就不比职业数学家差，他似乎对数论最有兴趣，亦对现代微积分的建立有所贡献。被誉为"业余数学家之王"。

 

 

 

尊重别人的劳动成果 转载请务必注明出处：https://www.cnblogs.com/5201351/p/17229709.html