排序 --> Python 实现
了解和实现冒泡排序、选择排序、插入排序、希尔排序、归并排序、和快速排序。
1.冒泡排序
冒泡排序要对一个列表多次重复遍历。
- 它要比较相邻的两项,并且交换顺序排错的项。
- 每对列表实行一次遍历,就有一个最大项排在了正确的位置。
- 大体上讲,列表的每一个数据项都会在其相应的位置“冒泡”。
它们的顺序是否正确。
- 如果列表有n项,第一次遍历就要比较n-1对数据。
- 需要注意,一旦列表中最大(按照规定的原则定义大小)的数据是所比较的数据对中的一个,
- 它就会沿着列表一直后移,直到这次遍历结束。
- 第二次遍历开始时,最大的数据项已经归位。
- 现在还剩n-1个待排数据项,即有n-2个要比较的数据对。
- 由于每一次遍历都会使下一个最大项归位,所需要遍历的总次数就是n-1。
- 完成n-1次遍历之后,最小的数据项一定已经归位,此时不需要再执行其他步骤。
def bubble_sort(alist):
n = len(alist)
# 外层循环控制比较几次
for i in range(n-1):
# 内存循环控制 第i次 交换 n-i 趟
# -i 是不再换前i次已经排好的
for j in range(n-i-1):
if alist[j] > alist[j+1]:
alist[j], alist[j+1] = alist[j+1], alist[j]
# print(alist)
由于冒泡排序要遍历整个未排好的部分,它可以做一些大多数排序方法做不到的事。
- 尤其是如果在整个排序过程中没有交换,我们就可断定列表已经排好。
- 因此可改良冒泡排序,使其在已知列表排好的情况下提前结束。
- 这就是说,如果一个列表只需要几次遍历就可排好,冒泡排序就占有优势:它可以在发现列表已排好时立刻结束。
- 改良版冒泡排序。它通常被称作“短路冒泡排序”。
def shortBubbleSort(alist):
n = len(alist)
# 外层循环控制比较几次
for i in range(n-1):
# 假设已经完全排好序
sorted = True
# 内存循环控制 第i次 交换 n-i 趟
# -i 是不再换前i次已经排好的
for j in range(n-1-i):
if alist[j] > alist[j+1]:
alist[j], alist[j+1] = alist[j+1], alist[j]
# 未完全排好序
sorted = False
if sorted: # 发现列表已排好时立刻结束
return
print(alist)
2.选择排序
选择排序提高了冒泡排序的性能,
- 它每遍历一次列表只交换一次数据,即进行一次遍历时找到最大的项,完成遍历后,再把它换到正确的位置。
- 和冒泡排序一样,第一次遍历后,最大的数据项就已归位,第二次遍历使次大项归位。
- 这个过程持续进行,一共需要n-1次遍历来排好n个数据,
- 因为最后一个数据必须在第n-1次遍历之后才能归位。
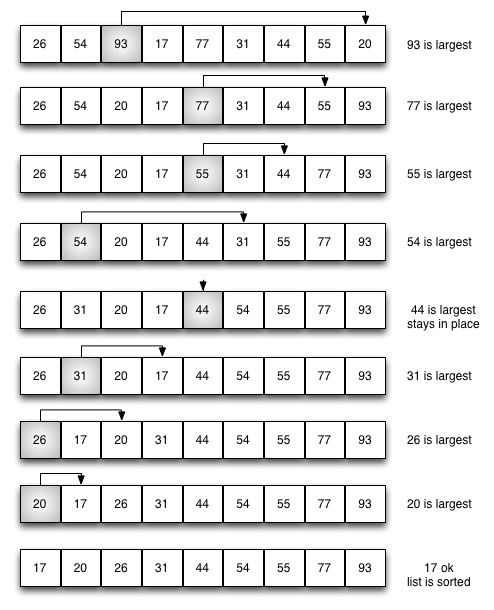
- 每一次遍历,最大的数据项被选中,随后排到正确位置。
- 第一次遍历排好了93,第二次排好了77,第三次排好了55,以此类推。
def selectionSort(alist):
# 外层控制比较几次,一共需要 n-1 次遍历来排好 n 个数据
for fillslot in range(len(alist)-1, 0, -1):
# 假设第一次元素就是最大值
position_max = 0
# 内层控制元素比较和更新索引
for location in range(1, fillslot+1):
# 进行比较
if alist[location] > alist[position_max]:
# 更新索引
position_max = location
# 退出循环后,交换数据
alist[fillslot], alist[position_max] = alist[position_max], alist[fillslot]
测试:
if __name__ == "__main__":
alist = [54, 26, 93, 17, 77, 31, 44, 55, 20]
print(alist)
selectionSort(alist)
print(alist)
3.插入排序
插入排序的算法复杂度仍然是O(n2),但其工作原理稍有不同。
- 它总是保持一个位置靠前的已排好的子表,
- 然后每一个新的数据项被“插入”到前边的子表里,排好的子表增加一项。
图4展示了插入排序的过程。阴影区域的数据代表了程序每运行一步后排好的子表。

- 我们认为只含有一个数据项的列表是已经排好的。
- 每排后面一个数据(从1开始到n-1),这个的数据会和已排好子表中的数据比较。
- 比较时,我们把之前已经排好的列表中比这个数据大的移到它的右边。
- 当子表数据小于当前数据,或者当前数据已经和子表的所有数据比较了时,就可以在此处插入当前数据项。
def insertionSort(alist):
# 外层循环控制 从右边第二个元素开始 向前面排好序的子列表中插入
for index in range(1, len(alist)):
pos = index
# 内存循环 依次从子列表的最后一个最大的元素 和 你要插入的元素比较
# 如果你的当前要插入的元素小,两个元素交换位置
while pos > 0 and alist[pos-1] > alist[pos]:
alist[pos], alist[pos - 1] = alist[pos-1], alist[pos]
pos -= 1
测试:
if __name__ == '__main__':
lst = [54, 26, 93, 17, 77, 31, 44, 55, 20]
print(lst)
insertionSort(lst)
print(lst)
4. 希尔排序
希尔排序有时又叫做“缩小间隔排序”,它以插入排序为基础,将原来要排序的列表划分为一些子列表,再对每一个子列表执行插入排序,从而实现对插入排序性能的改进。划分子列的特定方法 是希尔排序的关键。我们并不是将原始列表分成含有连续元素的子列,而是确定一个划分列表的增量“i”,这个i更准确地说,是划分的间隔。然后把每间隔为i 的所有元素选出来组成子列表。

这里有一个含九个元素的列表。
- 如果我们以3为间隔来划分,就会分为三个子列表,每一个可以执行插入排序。
- 这三次插入排序完成之后,虽然这个列表还没有完全排好序,
- 但有趣的是,经过我们对子列的排序之后,列表中的每个元素更加靠近它最终应该处在的位置。
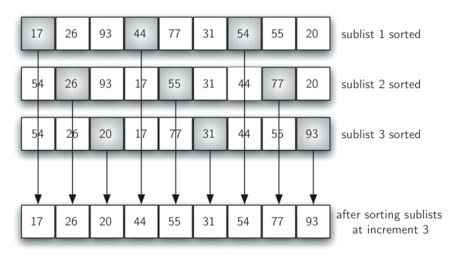
- 最终以1为间隔进行插入排序,即标准的插入排序的过程。
- 注意到,通过对前面子列进行排序之后,我们减少了将原始列表排序时需要比对和移动的次数。
在这个例子中,我们仅需要再进行四次移动就可以完成排序。

- 特定选取划分间隔的方法是希尔排序的独特之处。
- 代码1中的函数使用了一组不同的间隔。
- 在这个例子中,我们从含2个元素的子列开始排序;
- 下一步排含4个元素的子列。
- 最终,整个数列用基本的插入排序排好。
def shellSort(alist):
# 我们从含2个元素的子列开始排序, 子列表的数目 就是列表长度的一半
sublistcount = len(alist)//2
while sublistcount > 0:
# 每个子列表执行插入排序
for startpostion in range(sublistcount):
# 间隔正好是 子列表的数量
print("alist: %s" % alist, "startpostion: %d" % startpostion, "sublistcount %d" % sublistcount)
gapInsertionSort(alist, startpostion, sublistcount)
print("After increments of size", sublistcount, "The list is", alist)
sublistcount = sublistcount // 2
def gapInsertionSort(alist, start, gap):
for i in range(start+gap, len(alist), gap):
pos = i
while pos >= gap and alist[pos-gap] > alist[pos]:
alist[pos], alist[pos-gap] = alist[pos-gap], alist[pos]
pos -= gap
测试:
if __name__ == '__main__':
# 奇数次第一组第一次是三个元素 [54,77,20]
# alist = [54, 26, 93, 17, 77, 31, 44, 55, 20]
# 偶数次比较好看
alist = [54, 26, 93, 17, 77, 31, 44, 55]
shellSort(alist)
print(alist)
缩减版:
def shell_sort(lst):
step = int(len(lst)/2)
while step > 0:
for i in range(step, len(lst)):
while i >= step and lst[i] < lst[i - step]:
lst[i], lst[i - step] = lst[i - step], lst[i]
i -= step
step = int(step/2)
print(lst)
alist = [54, 26, 93, 17, 77, 31, 44, 55, 20]
shell_sort(alist)
- 乍一看,你可能会觉得希尔排序不会比插入排序要好,因为它最后一步执行了一次完整的插入排序。
- 但事实上,最后的一次排序并不需要很多次的移动,
- 因为正如上面所讨论的,这个列表已经在之前的对子列的插入排序中实现了部分排序。
- 换句话说,每个步骤使得这个列表与原来相比更趋于有序状态。这使得最后的排序非常高效。
对希尔排序的综合算法分析已经远超出讨论范围,基于对该算法的描述,
- 我们可以说它的时间复杂度大致介于O(n)和O(n2)之间。
- 如果使用某些间隔时,它的时间复杂度为O(n2)。
- 通过改变间隔的大小,比如以2k-1(1,3,5,7,15,31等等)为间隔,希尔排序的时间复杂度可以达到O(n3/2)。
5.归并排序
我们现在把注意力转移到用分而治之的策略来改进排序算法的表现。
- 我们要学的第一种算法就是归并排序。
- 归并排序是一种递归算法,它持续地将一个列表分成两半。
- 如果列表是空的或者只有一个元素,那么根据定义,它就被排序好了(最基本的情况)。
- 如果列表里的元素超过一个,我们就把列表拆分,然后分别对两个部分调用递归排序。
- 一旦这两个部分被排序好了,那么这种被叫做归并的最基本的操作,就被执行了。
- 归并是这样一个过程:把两个排序好了的列表结合在一起组合成一个单一的,有序的新列表。
- 图10就展示了我们熟悉的作为例子的列表如何被归并排序算法拆分,
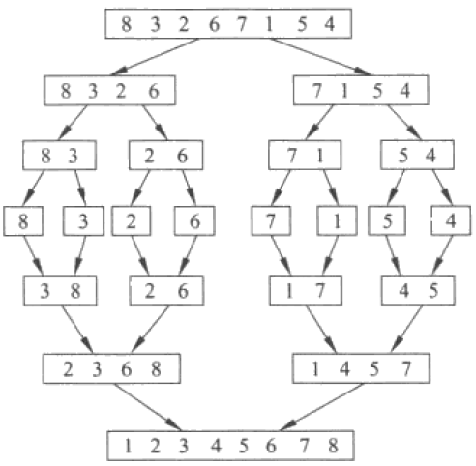
def merge_sort(alist):
n = len(alist)
# 递归结束条件
if n <= 1:
return alist
# 中间位置
mid = n // 2
# 递归拆分左侧
left_lst = merge_sort(alist[:mid])
# 递归拆分右侧
right_lst = merge_sort(alist[mid:])
return merge(left_lst, right_lst)
def merge(left, right):
print(left, right)
# 需要两个游标,分别指向左列表和右列表的第一个元素
left_point, right_point = 0, 0
# 定义最终返回的结果集
result = []
# 循环合并数据
while left_point < len(left) and right_point < len(right):
# 谁小放前面
if left[left_point] <= right[right_point]:
# 放入结果集
result.append(left[left_point])
# 游标移动
left_point += 1
else:
result.append(right[right_point])
right_point += 1
# print("合并数据后:", result)
# print('left: ', left[left_point:])
# print('right: ', right[right_point:])
# 退出循环时,形成左右两个序列
result += left[left_point:]
result += right[right_point:]
return result
if __name__ == '__main__':
li = [54, 26, 93, 17, 77, 31, 44, 55, 20]
lst = [8, 3, 2, 6, 7, 1, 5, 4]
print(lst)
sort_lst = merge_sort(lst)
print(lst)
print(sort_lst)
为了分析归并算法,我们需要考虑它实施的两个不同步骤。
- 第一步,列表被拆分,我们已经(在二分查找中)计算过,我们能通过logn的数量级的计算将长度为n的列表拆分。
- 而第二个过程是合并。
- 每个列表中的元素最终将被处理并被放置在排序好的列表中,所以合并操作对一个长度为n的列表需要n的数量级的操作。
- 因此分析结果就是,拆分需要logn数量级的操作
- 而每次拆分需要n数量级的操作因此最终操作的复杂度为nlogn。
- 归并排序是一种O(nlogn) 的算法。
6.快速排序
快速排序用了和归并排序一样分而治之的方法来获得同样的优势,但同时不需要使用额外的存储空间。
经过权衡之后,我们发现列表不分离成两半是可能的,当这发生的时候,我们可以看到,操作减少了。
- 快速排序首先选择一个中值。虽然有很多不同的方法来选择这个数值,我们将会简单地选择列表里的第一项。
- 中值的作用在于协助拆分这个列表。
- 中值在最后排序好的列表里的实际位置,我们通常称之为分割点的,是用来把列表变成两个部分来随后分别调用快速排序函数的。
快速排序算法的工作原理如下:
- 从数列中挑出一个元素,称为"基准"(pivot)。
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。
- 在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。

# first 理解为第一个位置的索引,last 是最后位置索引
def quick_sort(alist, first, last):
# 递归中止条件
if first >= last:
return
# 设置第一个元素为中间值
mid_value = alist[first]
# low 指向
low = first
# high
high = last
# 只要 low 小于 high 就一直走
flag = 0
while low < high:
# high 大于中间值,则进入循环
while low < high and alist[high] >= mid_value:
# high 往左走
high -= 1
# 出循环后,说明high小于中间值,low指向该值
alist[low] = alist[high]
# low 小于中间值,则进入循环
while low < high and alist[low] < mid_value:
# low 往右走
low += 1
# 出循环后,说明low 大于中间值,high 指向该值
alist[high] = alist[low]
if not flag:
print(alist)
# 退出整个循环后,low 和 high 相等
# 将中间值放到中间位置
alist[low] = mid_value
print(alist)
flag = 1
# 递归
# 先对左侧快排
quick_sort(alist, first, low-1)
# 对右侧快排
quick_sort(alist, low+1, last)
测试:
if __name__ == "__main__":
lst = [54, 26, 93, 17, 77, 31, 44, 55, 20]
print("原来的list:\n", lst)
quick_sort(lst, 0, len(lst) - 1)
print("快速排序后的list: \n", lst)
# python 风格的简易版本
def quick_sort_simple(array): if len(array) < 2: return array else: pivot = array[0] less = [i for i in array[1:] if i < pivot] greater = [i for i in array[1:] if i > pivot] return quick_sort_simple(less) + [pivot] + quick_sort_simple(greater) if __name__ == "__main__": lst = [54, 26, 93, 17, 77, 31, 44, 55, 20] print("原来的list:\n", lst) sorted_list = quick_sort_simple(lst) print("快速排序后的list: \n", sorted_list)
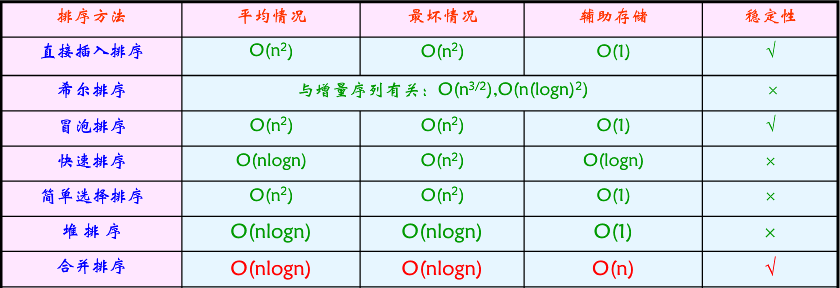
各种排序方法的比较: