索引OFDM调制解调系统的matlab性能仿真
1.算法仿真效果
本文所进行的仿真工作是《m索引OFDM调制解调系统的性能仿真分析》基础上做了完善。
首先仿真图的增减,可以对比两篇文章的仿真图,多出来的仿真图就是增加的内容。
另外对仿真过程的视频操作过程,配上了语音介绍(老版本操作视频不带语音)。
matlab2022a仿真结果如下(完整代码运行后无水印):
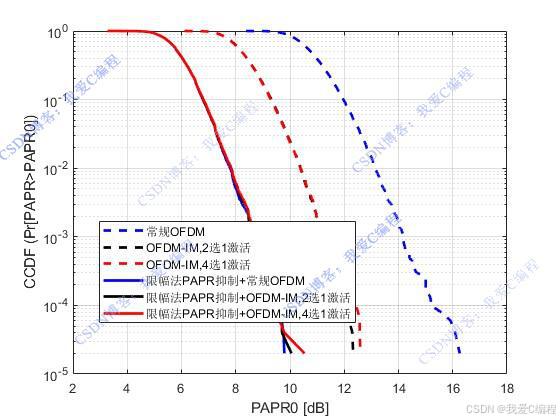
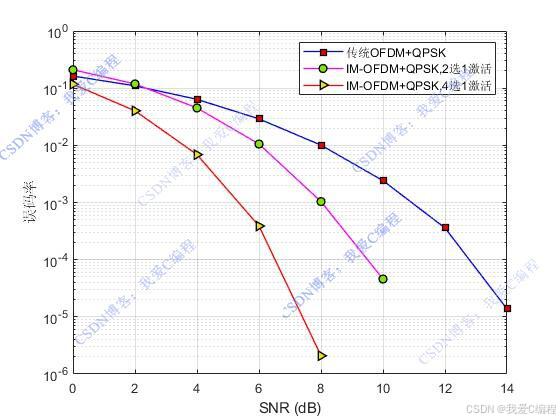
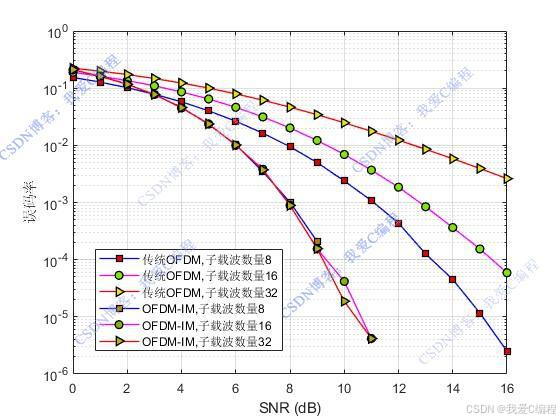
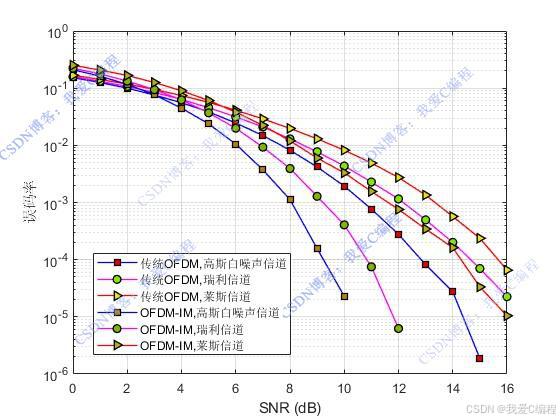
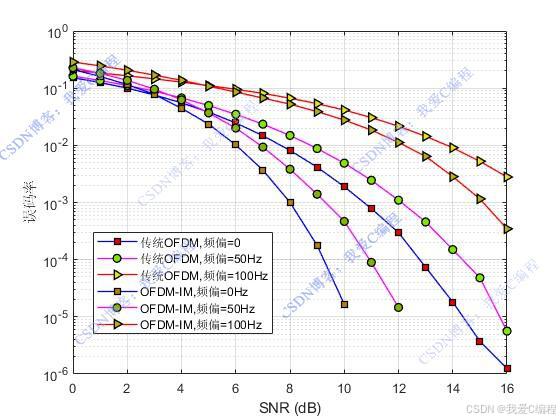
仿真操作步骤可参考程序配套的操作视频。
2.算法涉及理论知识概要
正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)是一种广泛应用于无线通信的技术,它通过将高速串行数据流分解为多个低速并行子载波来提高系统的抗多径干扰能力。然而,传统的OFDM技术在某些情况下仍存在一些不足,例如峰均功率比(PAPR)高、频谱利用率受限等问题。为了克服这些缺点,索引OFDM-IM(Index Modulation for OFDM, OFDM-IM)被提出,它结合了传统OFDM和空间调制的思想,进一步提高了系统的性能。
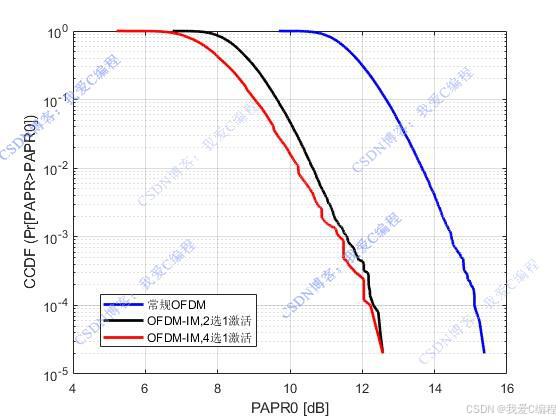
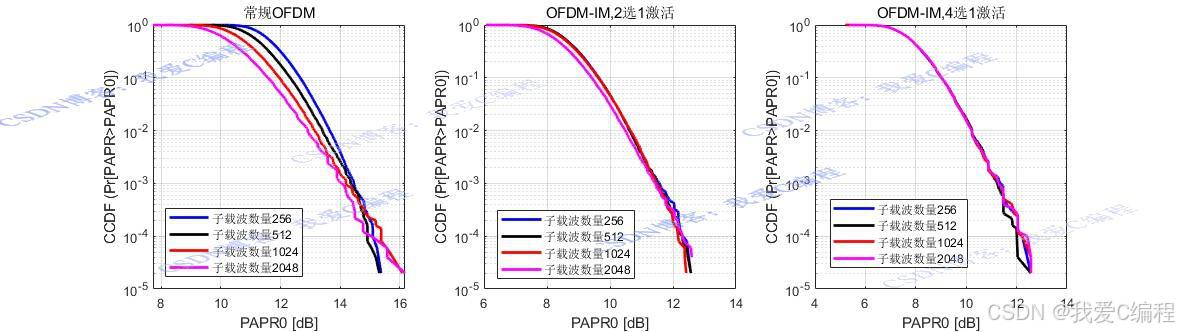
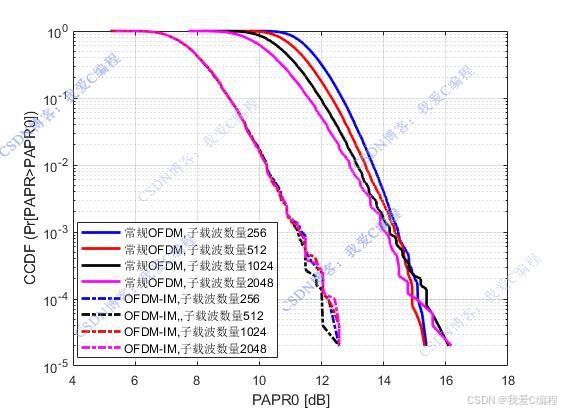
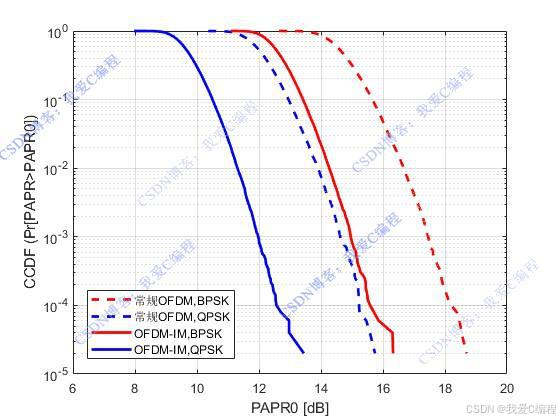
OFDM-IM的核心思想是通过激活不同的子载波组合来传输额外的信息,从而提高频谱效率和降低PAPR。
基于索引调制的OFDM(OFDM-IM,OFDM with Index Modulation)技术被提出,在频率选择性衰落信道上提升了系统的分集增益,特别是在较低频谱效率场景下能够有效降低系统的误比特率。在OFDM-IM方法中,特殊的索引信息传输方式以及索引结构的设计对分集增益的提高,引发了广泛的关注。如何通过索引结构的设计,取得比OFDM更低的误比特率以及更高的频谱效率成为了索引调制OFDM研究方向上的热点。
主要研究工作内容如下:
(1)针对OFDM中索引调制技术存在频谱效率较低的问题,本文提出了OFDM联合子块索引调制技术(OFDM-JS-IM,OFDM with Joint Subblock Index Modulation),将索引映射中被丢弃部分索引组合,在联合子块空间中进行了重复利用。仿真验证及理论分析表明,OFDM-JS-IM方法能够以轻微的误比特率性能损失为代价,有效提高OFDM-IM的频谱效率。
(2)针对索引结构与分集性能的关系进行了分析。由于OFDM-IM的特殊结构,索引比特的分集阶数高于一般的符号比特,使得OFDM-IM性能优于OFDM。然而,OFDM中的索引调制结构也仅仅能将部分比特的分集阶数提高至2。本文提出了OFDM全索引方法(OFDM with All Index Modulation,OFDM-AIM),不再使用低分集阶数的符号比特传输信息,而将所有信息以索引比特的方式传输,并提出了提高子块分集阶数的搜索算法,能够构建具有高分集阶数的合法子块集合。仿真结果表明,该方法能够有效提升系统的分集增益。
(3)基于上述OFDM-AIM技术,本文还提出了可变子块长度的子块设计辅助的OFDM-AIM。由于OFDM-AIM中子块长度决定了系统的最高分集阶数,因此可以适当提高子块长度以寻找更多较高分集阶数的子块,以提高分集增益。根据系统的频谱效率和计算复杂度要求,该方法能通过变化子块长度在实际应用中达到更好的性能权衡。
(4)分集阶数只是评价发射端信号的特性,而系统的误比特率性能不仅与分集阶数有关,还与不同子块符号间的欧式距离以及信道特性有关。针对该问题,本文将启发式算法中的遗传算法用于搜索具有最低误比特率的子块查找表。
但是,在高速场景下,子信道间的正交性会受到多普勒频移的破坏而引起载波间干扰,并且ofdm多个子信道信号叠加也会导致较高的峰均比,这些缺点时ofdm不适用于高速场景。而基于索引调制的正交频分复用(ofdm-im)技术将空间调制技术与传统的正交频分复用(ofdm)技术相结合,其思想是不仅激活子载波可以传输调制信号,而且可以传输其静默子载波的位置信息,从而弥补静默子载波不发送数据造成的损失。静默子载波的存在使得多普勒频移所带来的子载波间的干扰降低,使得系统对频偏不敏感。同时,大量静默子载波的存在又降低了整个输出符号的峰均比,这些优点使得索引调制技术成为5g研究热点之一。
OFDM-IM技术和传统的OFDM技术不同之处在于其在调制阶段,加入了索引调制步骤,根据索引调制比特信息,通过映射关系表,选择子载波进行激活并发送相应的比特数据,而未被选择的子载波则处于静默状态。这些索引调制比特数据同时补偿未被激活的静默子载波产生的频谱利用率低的问题。而在OFDM-IM接收部分,则通过子载波块的检测模块来恢复出索引信息和数据符号信息。
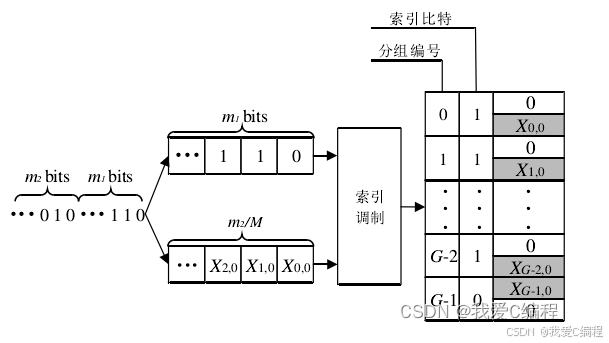
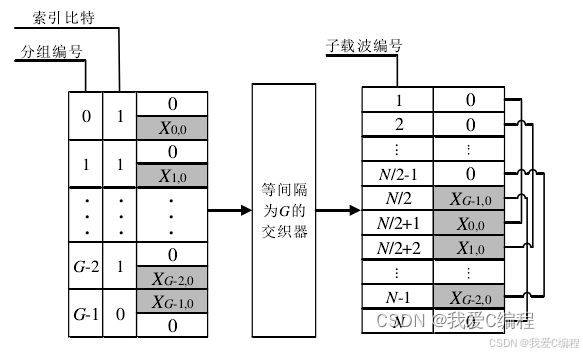
如上所示,OFDM-IM调制系统主要有两种调制方式,一种是相邻分块的调制方式(如图1所示),一种是交织调制方式(如图2所示)。从图1和图2可知,基于相邻分块的调制方式,其主要通过子载波以相邻的方式进行分块划分,而基于交织分块的调制方式,其通过在频域上加入一个交织深度为G的等间隔交织器来实现分块划分。
OFDM-IM索引调制系统相对于传统的OFDM系统而言,其最要区别在于被激活的子载波数量被降低,因此其对子载波数量相对于OFDM系统而言较为稀疏,那么其对频偏更加的不敏感。另外一方面,通过OFDM-IM索引调制技术,则可以在传统OFDM调制系统的基础上加入一个调制域,补偿未被激活的子载波带来的频谱利用率方面的损失,从而起到提高频谱利用率,提升系统误码率性能的需求。
3.MATLAB核心程序
%子载波数量
Nsub = 2048;
%子块
G = 16; %2个子载波作为一个块
Phase_Set = [1 -1];
Nlength = 50000;%数据长度
PAPR_SLM = zeros(3,Nlength);
BPSK = 1;%BPSK调制
X = zeros(1,Nsub);
for ij=1:Nlength%开始循环仿真
ij
%产生数据bit信息
bitsource = rand(1,Nsub)>=0.5;
%产生索引比特
index = rand(1,Nsub)>=0.5;
%调制,在调制过程中加入单个索引的调制方式
X0 = modulation(bitsource,BPSK);
X = reshape(X0,[G,Nsub/G]);
Xindex = reshape(index,[G,Nsub/G]);
X2 = zeros(G,2*Nsub/G);
for i=1:G
%选择前面4个作为索引比特
IMtable = Xindex(i,:);
S = X(i,:);
for j = 1:length(S)
if IMtable(j) == 1
X2(i,2*j-1) = S(j);
X2(i,2*j) = 0;
else
X2(i,2*j-1) = 0;
X2(i,2*j) = S(j);
end
end
end
X3 = reshape(X2',[1,2*Nsub]);
%IFFT
x = ifft(X3,[],2);
%计算PAPR
Signal_Power = abs(x.^2);
%PTS
K = 128; % SIZE OF FFT
V = 4;
Choose_Len=16;
A = zeros(V,K);
Choose = [1 1 1 1; 1 1 1 2; 1 1 2 1; 1 2 1 1; 2 1 1 1;
1 1 2 2; 1 2 1 2; 1 2 2 1; 2 2 1 1; 2 1 2 1; 2 1 1 2;
2 2 2 1; 2 2 1 2; 2 1 2 2; 1 2 2 2; 2 2 2 2];
for v=1:V
A(v,v:V:K) = X(v:V:K);
end
a = ifft(A,[],2); %行变化,默认为列变化
min_value = 10;
for n=1:Choose_Len
temp_phase = Phase_Set(Choose(n,:)).';
temp_max = max(abs(sum(a.*repmat(temp_phase,1,K))));
if temp_max<min_value
min_value = temp_max;
Best_n = n;
end
end
aa = sum(a.*repmat(Phase_Set(Choose(Best_n,:)).',1,K));
Signal_Power = abs(aa.^2);
Peak_Power = max(Signal_Power,[],2);
Mean_Power = mean(Signal_Power,2);
PAPR_Orignal(ij) = 10*log10(Peak_Power./Mean_Power);
end
[cdf1, PAPR1] = ecdf(PAPR_Orignal);
%显示PAPR
figure;
semilogy(PAPR1,1-cdf1)
xlabel('PAPR0 [dB]');
ylabel('CCDF (Pr[PAPR>PAPR0])');
grid on
save R1imPTS.mat PAPR1 cdf1
0sj_016m



 浙公网安备 33010602011771号
浙公网安备 33010602011771号