m基于遗传优化的LDPC码NMS译码算法最优归一化参数计算和误码率matlab仿真

1.算法仿真效果

matlab2022a仿真结果如下：

 

遗传优化迭代过程：

 

 

 

误码率对比：

 

 

 

 

 

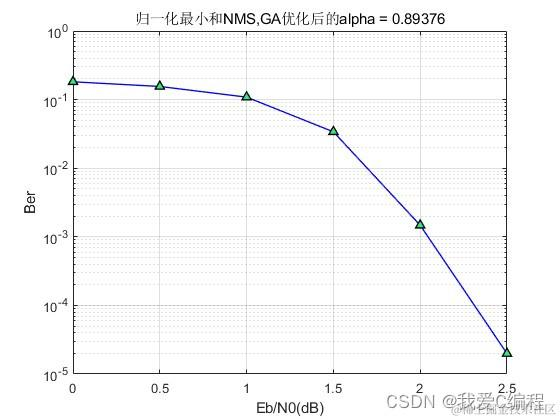
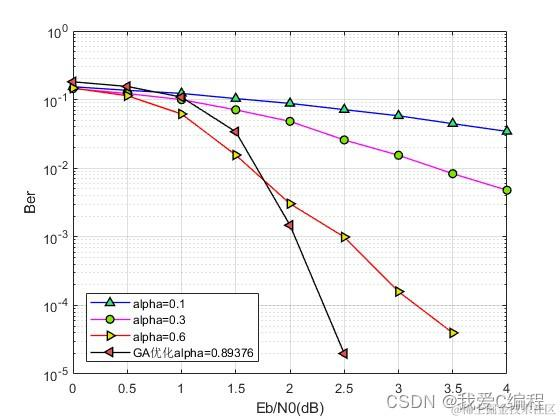
2.算法涉及理论知识概要

       低密度奇偶校验码(Low-Density Parity-Check Code, LDPC码)因其优越的纠错性能和近似香农极限的潜力，在现代通信系统中扮演着重要角色。归一化最小和(Normalized Min-Sum, NMS)译码算法作为LDPC码的一种高效软译码方法，通过调整归一化因子来改善其性能。而基于遗传优化的NMS译码算法最优归一化参数计算，旨在通过进化计算策略自动寻找最佳的归一化参数，进一步提升译码性能。

 

       LDPC码是由稀疏校验矩阵定义的一类线性分组码。其校验矩阵H具有较低的行和列权重，这使得使用迭代算法进行译码成为可能。NMS算法是基于最小和(Min-Sum, MS)算法的改进版本，旨在减小最小和算法的过估计问题。

 

      在NMS算法中，每个消息更新规则可以表示为：

 

 

 

        遗传算法(Genetic Algorithm, GA)是一种基于自然选择和遗传机制的全局搜索优化方法，适用于解决复杂的非线性优化问题。在基于遗传优化的NMS译码参数搜索中，归一化因子R被视为一个需要优化的基因，通过不断迭代的“选择”、“交叉”和“变异”操作，寻找使译码性能最优的R值。

 

       在迭代过程中，遗传算法通过不断探索搜索空间，逐渐逼近这个全局最优解。值得注意的是，归一化因子R的取值范围通常限制在(0, 1]区间内，因为过大的R可能导致消息放大失真，而过小的R则可能无法有效抑制过估计。

 

3.MATLAB核心程序

 

while gen < MAXGEN
      gen
      Pe0 = 0.999;
      pe1 = 0.001; 
 
      FitnV=ranking(Objv);    
      Selch=select('sus',Chrom,FitnV);    
      Selch=recombin('xovsp', Selch,Pe0);   
      Selch=mut( Selch,pe1);   
      phen1=bs2rv(Selch,FieldD);   
 
      for a=1:1:NIND  
          X           = phen1(a,:);
          %计算对应的目标值
          [epls]      = func_obj(X);
          E           = epls;
          JJ(a,1)     = E;
      end 
      
      Objvsel=(JJ);    
      [Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel);   
      gen=gen+1; 
 
 
      Error2(gen) = mean(JJ);
end 
figure
plot(Error2,'linewidth',2);
grid on
xlabel('迭代次数');
ylabel('遗传算法优化过程');
legend('Average fitness');
 
................................................................................
fitness=mean(Ber);
 
figure
semilogy(SNR, Ber,'-b^',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.2,0.9,0.5]);
 
xlabel('Eb/N0(dB)'); 
ylabel('Ber');
title(['归一化最小和NMS,GA优化后的alpha = ',num2str(aa)])
grid on;
save NMS4.mat SNR Ber Error2 aa