m根据给定系统传递函数自动绘制系统结构图matlab仿真,包括直接型,级联型以及并联型
1.算法仿真效果
matlab2022a仿真结果如下:
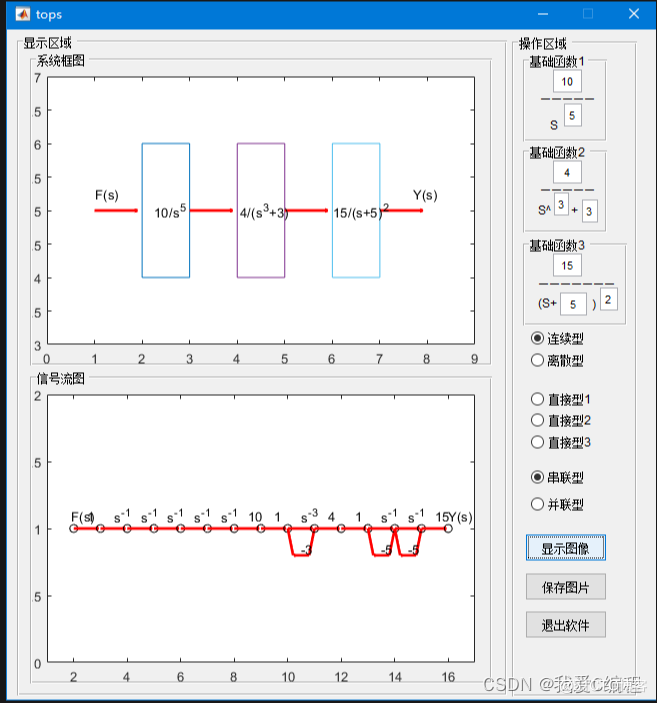

2.算法涉及理论知识概要
在控制系统分析和设计过程中,传递函数是一个重要的概念。通过传递函数,我们可以快速地分析系统的稳定性、响应特性等。同时,根据系统传递函数自动绘制系统结构图是一项非常有价值的技术,它可以帮助工程师更好地理解和设计复杂的控制系统。本文将详细介绍根据给定系统传递函数自动绘制系统结构图的方法,包括直接型、级联型以及并联型。我们将首先介绍传递函数的基本概念,然后分别讨论直接型、级联型和并联型系统结构图的绘制方法,最后对比本文提出的自动绘制算法与其他相关算法的优缺点。
1. 传递函数基本概念
传递函数(Transfer Function)是一个描述线性时不变系统(Linear Time-Invariant System, LTI系统)输入输出之间关系的数学模型。它的定义如下:
G(s) = \frac{Y(s)}{X(s)}
其中,G(s)为系统的传递函数,Y(s)和X(s)分别表示系统输出和输入的拉普拉斯变换。传递函数可以很方便地用于分析系统的频域特性,例如稳定性、相位裕量、增益裕量等。
2. 系统结构图的绘制方法
2.1 直接型系统结构图
直接型系统结构图是最简单的一种结构图,它将传递函数直接表示为各个子系统的传递函数之积。给定一个传递函数G(s),我们可以将其表示为:
G(s) = G_1(s)G_2(s)\cdots G_n(s)
其中,G_i(s)表示第i个子系统的传递函数。要绘制直接型系统结构图,我们只需将各个子系统的传递函数依次连接即可。具体步骤如下:
将传递函数G(s)分解为各个子系统的传递函数之积;
依次绘制各个子系统,将其输入端连接到上一个子系统的输出端,输出端连接到下一个子系统的输入端。
这种方法的优点是简单直观,容易实现;缺点是对于复杂的传递函数,直接型结构图可能不是最简洁的表示形式。
2.2 级联型系统结构图
级联型系统结构图是一种将传递函数表示为若干个子系统传递函数级联连接的结构图。对于一个传递函数G(s) ,我们可以将其表示为:
G(s) = G_1(s) + G_2(s) + \cdots + G_n(s)
其中,G_i(s)表示第i个子系统的传递函数。要绘制级联型系统结构图,我们需要将各个子系统的传递函数相加,然后将结果与其它子系统的传递函数级联连接。具体步骤如下:
将传递函数G(s)分解为各个子系统的传递函数之和;
依次绘制各个子系统,将其输入端连接到上一个子系统的输出端,输出端连接到下一个子系统的输入端;
将所有子系统的输出端连接到一个求和器,求和器的输出即为系统输出。
这种方法的优点是可以表示更复杂的传递函数,适用于多个子系统相互影响的情况;缺点是结构图可能较为复杂,不易于理解和分析。
2.3 并联型系统结构图
并联型系统结构图是将传递函数表示为若干个子系统传递函数并联连接的结构图。对于一个传递函数G(s),我们可以将其表示为:
G(s) = \frac{G_1(s)G_2(s) + G_3(s)G_4(s) + \cdots + G_{2n-1}(s)G_{2n}(s)}{G_{2n+1}(s)}
其中,G_i(s)表示第i个子系统的传递函数。要绘制并联型系统结构图,我们需要将各个子系统的传递函数两两相乘,然后将结果相加,并与其它子系统的传递函数并联连接。具体步骤如下:
将传递函数G(s)分解为各个子系统的传递函数之商;
依次绘制各个子系统,将其输入端连接到上一个子系统的输出端,输出端连接到下一个子系统的输入端;
将所有子系统的输出端连接到一个求和器,求和器的输出即为系统输出;
将求和器的输出连接到另一个子系统($G_{2n+1}(s)$)的输入端,该子系统的输出即为总系统输出。
这种方法的优点是可以表示更复杂的传递函数,适用于多个子系统相互影响的情况;缺点是结构图可能较为复杂,不易于理解和分析。
3. 实现过程
实现根据给定系统传递函数自动绘制系统结构图的主要步骤如下:
对给定的传递函数进行因式分解,得到各个子系统的传递函数;
根据所需的结构图类型(直接型、级联型或并联型),按照相应的绘制方法将各个子系统连接起来;
用图形表示法绘制出系统结构图。
在实现过程中,我们需要解决以下关键问题:
传递函数因式分解:对于给定的传递函数,我们需要将其分解为各个子系统的传递函数。这可以通过使用数学软件(如MATLAB、Mathematica等)或编写专门的分解算法来实现。
子系统表示:在绘制系统结构图时,我们需要用图形表示法表示各个子系统。这可以通过使用绘图库(如Matplotlib、Graphviz等)或编写专门的绘图程序来实现。
3.MATLAB核心程序
if option2==2
axes(handles.axes2);
[xy1]=func_s1(a1,n1,0,1,option1);
hold on
[xy2]=func_s2(a2,b2,n2,xy1(end,1)-2,1,option1);
hold on
[xy3]=func_s3(a3,b3,n3,xy2(end,1)-2,1,option1);
hold on
[xend,I1] = max([xy1(end,1),xy2(end,1),xy3(end,1)]);
[yend,I2] = min([xy1(end,2),xy2(end,2),xy3(end,2)]);
xlim([1,xend+1]);
ylim([0,2]);
[x0,y0]=func_block(0,0);
[x0a,y0a]=func_block(2,0);
[x0b,y0b]=func_block(4,0);
if option1 == 1
text(x0(1)-0.1,1.1,['F(s)']);
text(xend,1.1,['Y(s)']);
else
text(x0(1)-0.1,1.1,['F(z)']);
text(xend,1.1,['Y(z)']);
end
%对应的系统框图%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
axes(handles.axes1);
[x0,y0]=func_block(0,0);
hold on
quiver(x0(1)-1,mean(y0),1,0,'r','filled','LineWidth',2);
hold on
quiver(x0(2),mean(y0),1,0,'r','filled','LineWidth',2);
hold on
if option1 == 1
text(mean(x0)*0.9,mean(y0),[num2str(a1),'/','s^',num2str(n1)]);
else
text(mean(x0)*0.9,mean(y0),[num2str(a1),'/','z^',num2str(n1)]);
end


 浙公网安备 33010602011771号
浙公网安备 33010602011771号