m基于matlab的GPS卫星信号捕获和数据解析仿真

1.算法描述

       全球定位系统(gps)是一种全天候、全球覆盖、高精度、自动化的卫星导航定位系统，该系统向有适当接收设备的全球范围用户提供精确、连续的三维位置和速度信息。gps自投入运行以来，已经发展成为一个涵盖各领域的服务系统。       

 

 

 

 

       卫星信号的捕获算法是卫星定位接收机的关键，传统的捕获算法通常采用基于fft的相干积分和非相干积分相结合的方法，例如在使用gps信号进行定位和导航前首先需要对卫星信号进行捕获，gps卫星信号的传统捕获算法一般为频域并行捕获算法，频域并行捕获算法的原理框图如图3所示，频域并行捕获算法是一种基于fft的捕获算法，搜索覆盖全部搜索频点和全部伪码序列，对于正常功率的gps信号，通常只需要处理lms的导航数据，就能够完成gps信号的捕获，但是对于gps弱信号而言，通常处理lms的导航数据所获得的判决量并不可靠，难以实现捕获，此时就需要通过增加捕获算法所用的数据长度，采用相关积分和非相关积分相结合的方法，来提高捕获灵敏度，但同时导致fft相关运算的计算量将成倍增长，从而造成捕获速度降低。

 

为了跟踪和解码GPS信号,首先要捕获到GPS信号。将捕获到的GPS信号的必要参数立刻传递给跟踪过程，再通过跟踪过程便可得到卫星的导航电文。GPS卫星处于高速运动中，因此，其频率会产生多普勒频移。载波频率与C/A码的多普勒频移将在下面详细讲述。

 

       GPS卫星发送的信号一般由3个分量组成：载波、伪码和导航电文，其中伪码和导航电文采用BPSK技术去调制载波。

 

       为了跟踪和解码GPS信号，首先要捕获到GPS信号。将捕获到的GPS信号的数据传递给跟踪过程，再通过跟踪过程便可得到卫星的导航电文。传统的GPS捕获方法有：串行搜索捕获、滑动相关法、循环相关法、PMF算法。

 

       GPS卫星信号是发生在两个L波段频率的载波信号L1和L2，两个载波频率分别是L1的主频率fL1和L2的次频率fL2。在L波段进行调制可以避免拥挤，因为L波段的频率占据使用比率和其他波段相比要低一些，有助于全球性观测；L波段上更容易进行扩频（将低比特率的电文转换成高比特率的组合码，有利于卫星信号的保密性），发送宽带信号；L波段大气偏差和电离偏差小，接收设备可以更简单、更经济地接收和测量。每一颗卫星均有唯一的扩频码或伪随机序列，由此调制出载波频率。

 

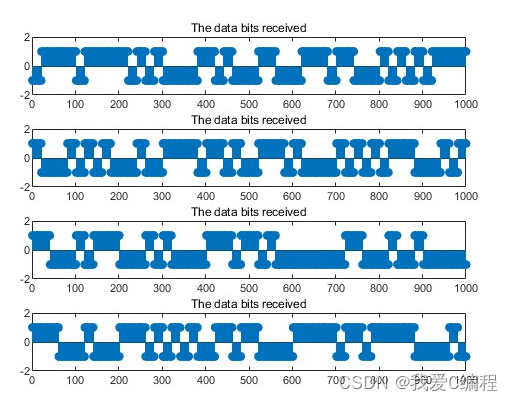
2.仿真效果预览

matlab2022a仿真结果如下：

 

 

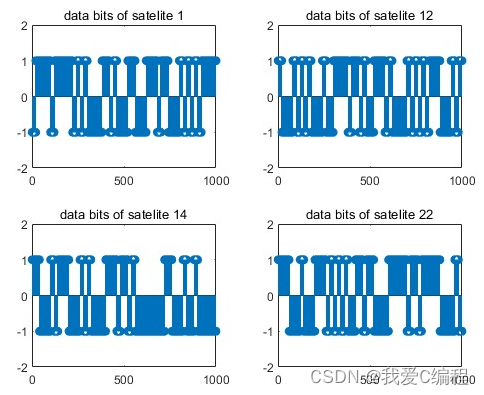
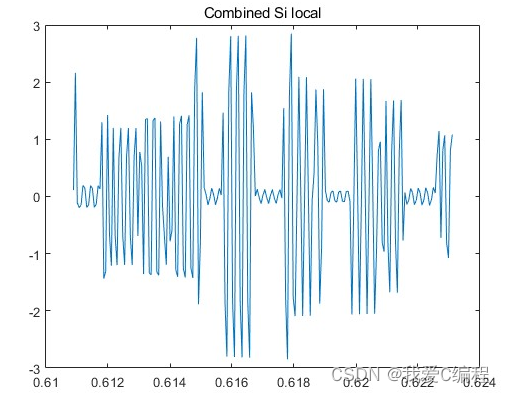
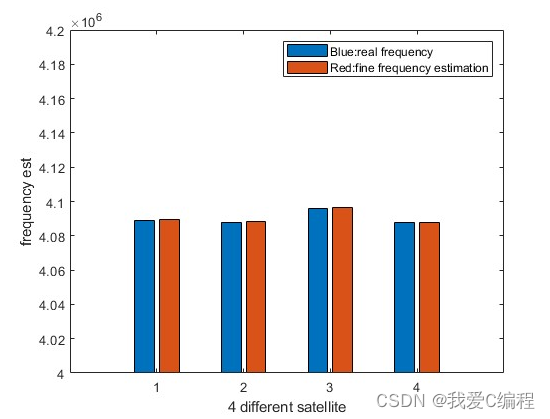
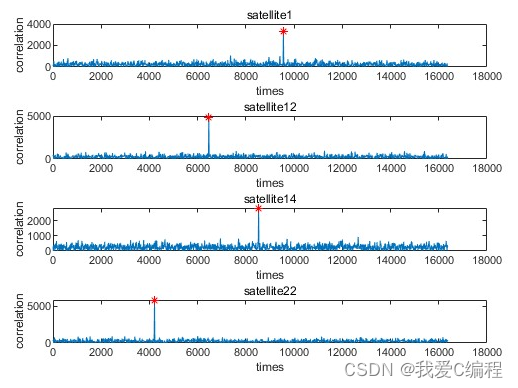
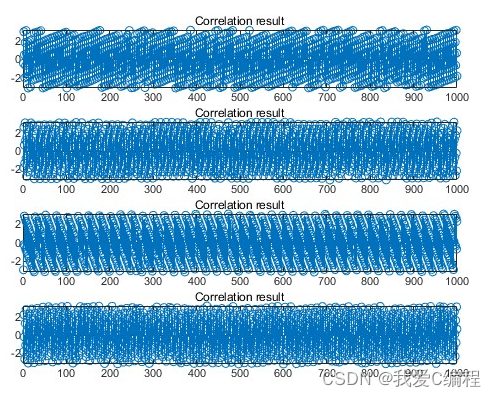
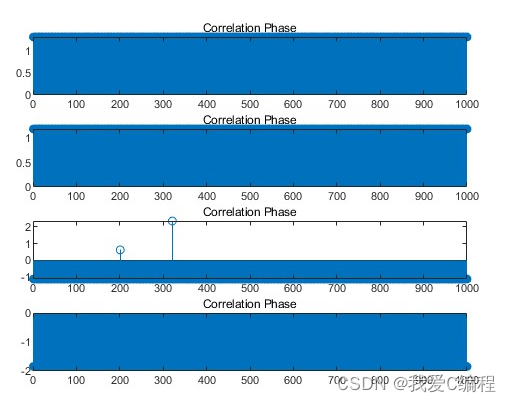
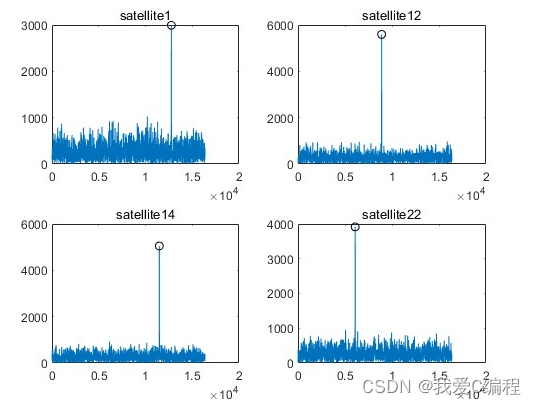
3.MATLAB核心程序

 

clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
 
rng('default')
%%
%11111111111111111111111111111111111111111111111111111111111
isnoise         = 0;%1:add noise;0 good signal
%nosie awgn
SNR             = -19;
 
%Q1
satellite       = [1,12,14,22];
satellitenumber = length(satellite);
fs              = 16.368e6; %sampling freq
IF              = 4.092e6;%centered
fIFD            = IF + 5e3 - 10e3*rand(1,satellitenumber);%no more than 5 KHz in absolute value
Fai             = 2*pi*rand(1,satellitenumber);%random values
Ai              = 0.7+0.3*rand(1,satellitenumber);%random between 1 and 0.7 for different satellites
taoi            = floor(4e5*rand(1,satellitenumber)) + 2e5; %random between 1 and 
Dur             = 20;%bit duration,20ms
Len             = 50;%data bit length,1s
%
CHIP_TIME       = 977.5e-9;    % chip time in seconds 
ts              = 1/fs;
n               = fs/1000; 
nn              = [0:n-1]; 
millisecond     = 1000;
 
x_bound         = (ts/2)/CHIP_TIME;  % Maximum offset 
d_samp          = 6; % sample offset between correlators 
d               = (d_samp*ts)/CHIP_TIME;  
msSamp          = 16368;
 
 
for i = 1:satellitenumber
    i
    %C
    %1ms with 16 samples
    code0   = digitizg(fs/1000,fs,0,satellite(i));
    %20ms
    code1   = [code0,code0,code0,code0,code0,code0,code0,code0,code0,code0,code0,code0,code0,code0,code0,code0,code0,code0,code0,code0];
    %len
    CA      = [];
    for j = 1:Len
        CA = [CA,code1];
    end
    %D
    Di0       = 2*double(rand(1,Len)>=0.5)-1;
    %output the data
    for j = 1:Len
        Dout2{i}(Dur*(j-1)+1:Dur*j) = Di0(j);
    end
    
    for j = 1:length(Dout2{i})
        Di2(length(code0)*(j-1)+1:length(code0)*j) = Dout2{i}(j);
    end
    %S
    signal0 = Ai(i).*CA.*Di2;
    %16times
    %delay taoi/61
    delays  = floor(taoi(i)/61);
    signal3 = [zeros(1,delays),signal0(1:end-delays)];
    
    %carrier
    t       = 0:1/fs:(length(signal3)-1)/fs;
    carrier{i} = cos(2*pi*fIFD(i)*t+Fai(i));
    Si0{i}     = signal3.*carrier{i};
end