m基于FH-GFSK信号的盲解调matlab仿真
1.算法描述
GFSK 高斯频移键控调制是把输入数据经高斯低通滤波器预调制滤波后,再进行FSK调制的数字调制方式。它在保持恒定幅度的同时,能够通过改变高斯低通滤波器的3dB带宽对已调信号的频谱进行控制,具有恒幅包络、功率谱集中、频谱较窄等无线通信系统所希望的特性。因此,GFSK调制解调技术被广泛地应用在移动通信、航空与航海通信等诸多领域中。
在无线通信中,为了对抗信道衰落和保证传输信息的安全常采用跳频(Frequency Hopping, FH)通信技术。高斯移频键控(Gauss Frequency Shift Keying, GFSK)具有恒幅包络、功率谱集中、频谱较窄等无线通信系统所希望的特性。FH-GFSK则结合了上述两种技术的优点,因此,在数字通信中得到广泛应用。
本课题采用基于GNU Radio的软件无线电接收机首先对FH-GFSK信号进行采集,随后对采集到的信号进行分析,最终实现信号的盲解调。
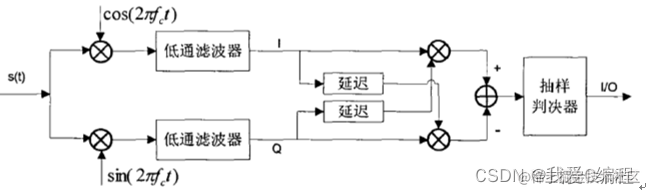
所以在进行盲估计时候,需要知道fc,和低通滤波器的参数,后面的是固定结构,就不用估计了。
然后题目中讲到:

高斯滤波器参数,实际上就是获得对应的低通滤波器;
然后调制指数的计算公式为:
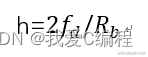
因此, 估计调制指数,实际上就是获得fd和Rb,而Rb表示符号速率,这个只要信号接收到,就可以得到的,不用估计,所以就是估计fd。FSK调制是载波的频率随信息符号成正比的一种调制方式,当发送信息符号1时发射频率向上搬移fdHz,当发送信息符号-1时发射频率向下搬移fdHz。 然后我们这里是调频通信,因此估计fd。
所以,这里,忙解调的参数估计,本质就是就是频率估计和滤波器参数估计两个部分。
常见的数字调制方法如:
ASK ——幅移键控调制,把二进制符号0和1分别用不同的幅度来表示。
FSK ——频移键控调制,即用不同的频率来表示不同的符号。如2KHz表示0,3KHz表示1。
GFSK——高斯频移键控,在调制之前通过一个高斯低通 滤波器来限制信号的频谱宽度。
GMSK——高斯滤波最小频移键控,是在MSK(最小频移键控)调制器之前插入高斯低通预调制滤波器的一种调制方式
2.仿真效果预览
matlab2022a仿真结果如下:
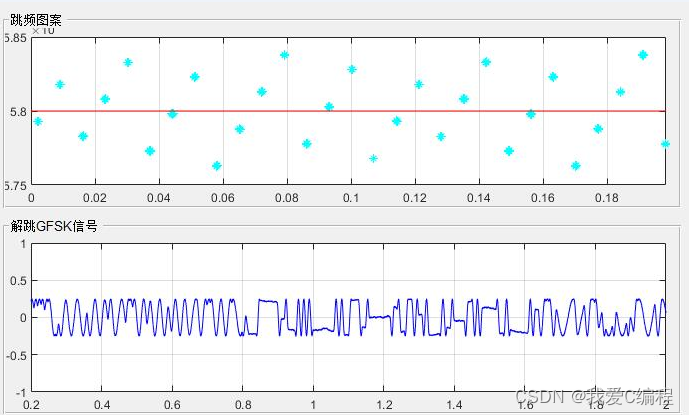


3.MATLAB核心程序
%滤波器估计值
%计算带宽,通过计算-3db频谱范围作为带宽
[x0,t,ssf,yy] = plotspec(Rx,1/fs);
Y2 = 10*log10(yy/max(yy));
Y3 = Y2(length(Y2)/2:end);
indx = find(Y3>=-3);
ssf2 = ssf(length(ssf)/2:end);
BB = (ssf2(indx(end))-ssf2(indx(1)));
BT = 100*BB/fs;
disp('调制指数');
set(handles.edit2,'string',num2str(BT));
Rfinal = [];
for i = 1:R
i
RR = selectRxFrame2(i,:);
[Isignal_,h] = glpfsignal(real(RR),fs,BT);
[Qsignal_,h] = glpfsignal(imag(RR),fs,BT);
%滤波这块比较费时,我这里只截取一部分进行处理
Isignal = Isignal_(1:length(RR));
Qsignal = Qsignal_(1:length(RR));
%输出二进制数据
tmps = Isignal.*[diff(Qsignal,1),0] - Qsignal.*[diff(Isignal,1),0];
%做下滤波处理
tmps = tmps-mean(tmps);
w = hamming(128);
tmps = conv(tmps,w);
tmps = tmps-mean(tmps);
Rfinal = [Rfinal,tmps];
end
tmps2= Rfinal>=0;
axes(handles.axes3);
plot(Rfinal)
axis([2000,20000,-2,3]);
axes(handles.axes4);
plot(tmps2)
axis([2000,20000,-1,2]);
01_153m



