【机器学习基础】——线性回归
之前看过一些有关机器学习的基础资料和视频，但很多知识点都记不太清了，现在专门开个专题，根据自己的理解将之前学过的进行回顾和整理，可能会引用一些例子和资料，资料主要来源于视频学习和《统计学习方法》一书，可能对于一些不清楚的问题会翻看一些博客等资料。
本节主要针对线性回归的原理以及梯度下降求解方法进行回顾。
线性回归
线性回归原理
线性回归是回归问题，不同于分类问题，线性回归的输出是一个scalar，即一个连续型的数值，即是给定一组数据{(x1，y1),(x2，y2),...,(xN，yN)}对数据进行回归分析，即对给定的数据进行拟合，找出最适合这组数据的一组参数w，b，从而拟合出方程y=wx+b，如图所示：
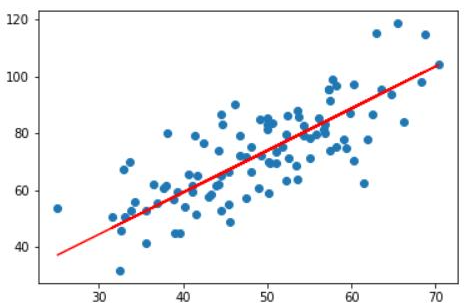
图上每个点就是一个数据，最终拟合出的红色的直线，这里的方程属于广义方程，并非简单的直线方程，后面会进一步解释。
既然线性回归属于机器学习一种方法，那么按照机器学习的三步走策略：
（1）给定一个模型及对应的一系列的模型参数（a set of function）
（2）找到一个衡量每个模型好坏的（goodness of function）
（3）从众多模型中选出一个最好的模型出来（training data）
下面我们结合一个具体的例子，对上面的步骤分别展开进行讨论，例子来源于李宏毅老师的机器学习的视频：
假设有10只宝可梦，就是10条训练数据，即属性分别是血量（hp）、身高（Height），体重（Weight）等，标签y为进化后的战斗力（combat pow，cp），我们希望通过这些属性对进化后的战斗力cp进行预测，即：
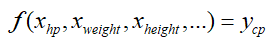
现在假设cp仅与hp有关，其他的属性暂时不考虑，即是一个二维的数据集，按照三步走的策略：
第一步a set of function：
给定一个模型集合，由于是线性回归，因此在二维空间中就是一条直线：
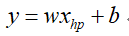
这里w，b可以取各种各样的值，即对应不同的模型，可以是如下这种：
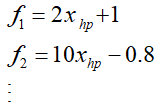
那么究竟哪种模型是最好的呢，这是我们需要给定一个衡量模型好坏的标准，因此进入
第二步goodness of function：
通常衡量模型好坏标准使用损失函数Loss Function，其输入是一个模型f，输出是这个模型f有不好，那么在线性回归中，如何定义LossFunction呢：
通常通过该模型的输出值与真实值之间的差别有多大作为损失，即平方损失或者绝对值损失两种，这里采用平方损失，即所有样本模型预测值与真实值之间差值的平方和，用ˆy表示真实值，f(x)表示模型的预测值，那么损失函数表示为：
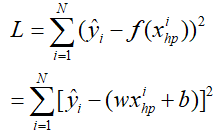
那么我们希望这样的损失越小越好，即找到一组参数w，b使得L最小，所得的w，b即与真实模型（这么说不恰当）是最接近的，即：
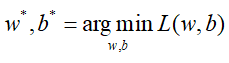
那么怎样找到这样一组参数呢？
第三步training data：
理论上根据所给定的数据集，穷举所有模型，依次代入模型，所求的最小的L即为最优参数w，b，但遗憾的模型所可能的取值并不能穷举。于是梯度下降可以对上述问题进行求解（后面会说为什么梯度下降），利用给定数据集，通过求解L分别w，b的求导，不断更新w，b朝着L减小的方向变化，直到结果收敛，这个过程就称之为线性回归的训练过程，即每次参数更新都朝着梯度的负方向移动，不断减小Loss的值，即更新规则为：
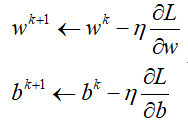
这里η为学习率learning_rate，即每次朝着Loss降低的方向移动的幅度，假设仅有一个参数w时，即Loss关于w的方程，那么上述过程放在图上即为：
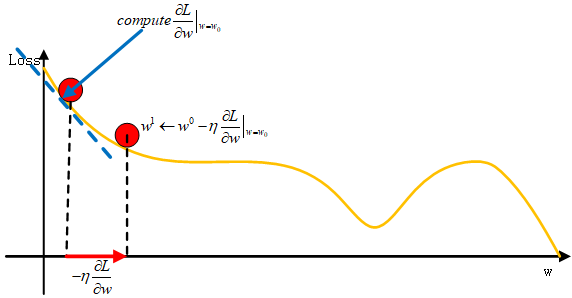
那么同时考虑w和b时，则就变成了下面这样：
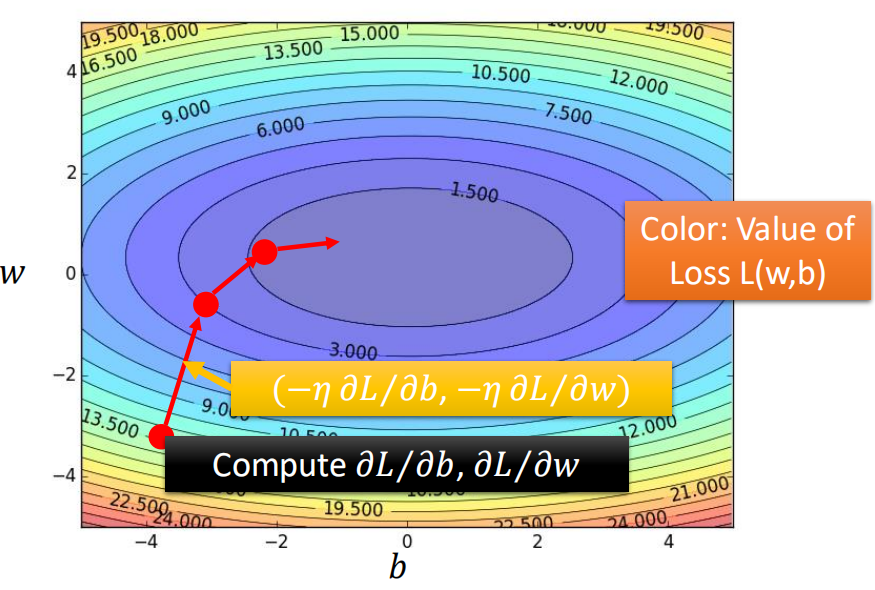这里有个问题，在用gradient descend的时候，当我们每次更新的时候是否一定会使得Loss下降呢？即：
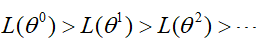
其实并不是这样，看下面这张图：
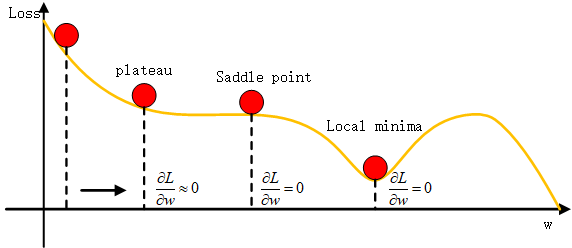
参数在更新的过程中，会陷入平原点和鞍点，此时导数几乎为0，可能不再更新了。
那么按照上面的算法的结果如何呢？
通过梯度下降，找到一组参数w=2.7，b=-188.4，然后带回到模型中，得到这样的一条直线：
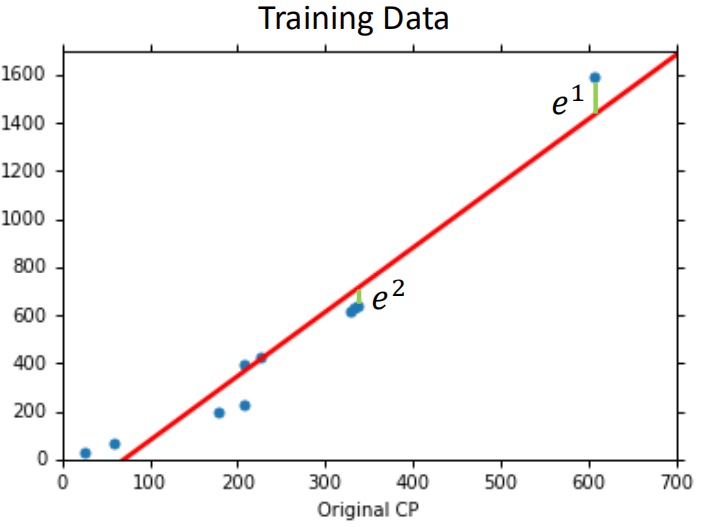
在训练集上的均方误差为31.9，在测试集上的均方误差为35。显然，这样的结果误差有点大，那么如何让结果能够更好呢？也就是说在上面三个步骤中，哪一步可以进一步优化呢？
首先是模型上，之前选用的是一次模型，那么现在换成二次呢？（注意，这里即使是二次，同样也是线性模型，相当于利用原先的特征构造出一个新特征出来），即：
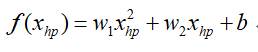
然后按照上面后面两个步骤依次更新参数w1,w2和b，再次训练数据集，拟合出一条二次曲线：
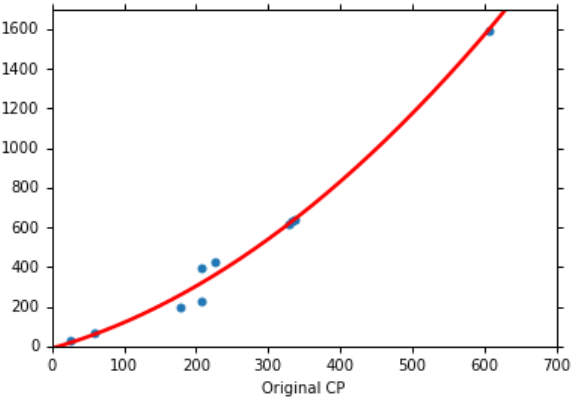
训练集在该模型的均方误差为15.4，在测试集上的均方误差为18.4，可以看到效果变好了，那我们能不能继续把拟合的曲线变得更复杂呢，即继续增加xhp的次数，3次方项、4次方项等等：
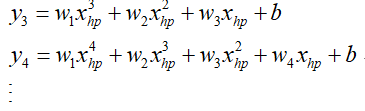
那么最终得到如下一组拟合结果：
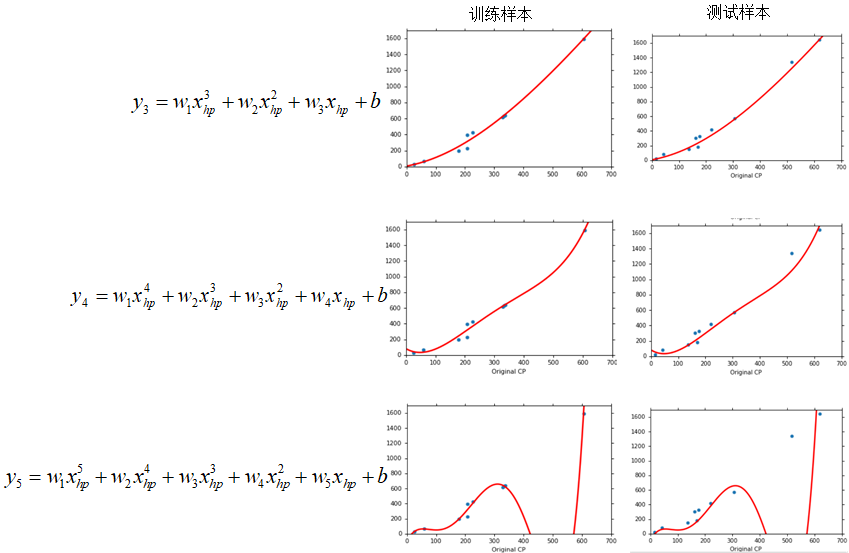
结果可以看出随着模型复杂程度的不断增加，在训练集上拟合效果越来越好，但是当模型增加到5次时，在测试集上的拟合效果就坏掉了，从所得到的误差数据来看：
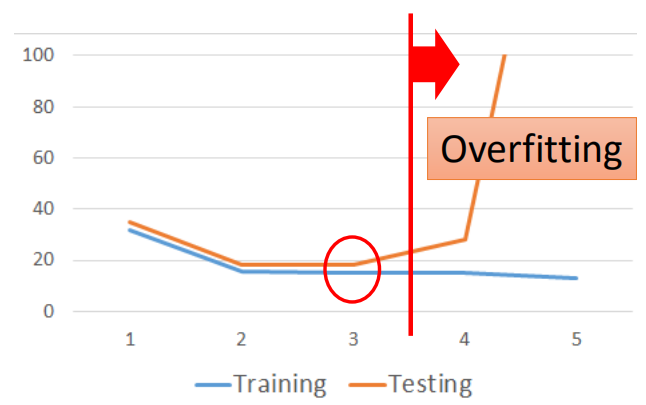
从数据可以看出，随着模型复杂度的不断提高，在训练集上的误差越来越小，而在测试集上则是先减小，然后陡增，这种情况称之为过拟合（overfitting），即：
上面的过程是只考虑了一个特征，如果将其他特征（weight，height等）考虑进去，并考虑每一个物种的类别，再重新设计模型：
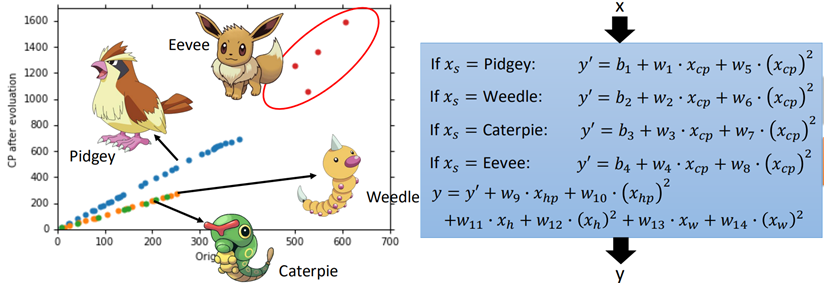
根据每个类别的样本（这里的分类其实只是为了理解线性模型而定的，实际中这样的类别可能在训练样本中并不存在，我们可以假想这也是一个特征，特征的不同取值属于不同的类别），再加上体重xw、身高xh特征，最终得到得到一个模型y，再进行训练，发现在训练集上的误差只有1.9，然而在测试集上为102.3，这仍然是过拟合状态。
Tips：上面说到，当特征为2次方、3次方等的时候该模型依旧是一个线性模型，其实高次项相当于是在建模过程中自己构建出来的一个全新的特征，可视作一个新的变量，因此，这样的模型也是线性模型。
回到上面，那么模型过拟合，我们该如何解决呢？即通过牺牲一定的在训练集上的误差，来减小在测试集上的误差呢？回到第二步，在度量模型好坏的指标上入手：
正则化
一种有效解决过拟合的方法就是正则化，即在损失函数中加入一定的代价函数，这种代价函数可以解释为先验知识，在优化误差函数的时候倾向于选择满足约束的梯度减少的方向，使最终的解倾向于符合先验知识（来自于百科）。
正则化有L1正则和L2正则，这里主要说一下L2正则，后面有时间对正则化进行单独讨论，先看对原损失函数加上L2正则项：
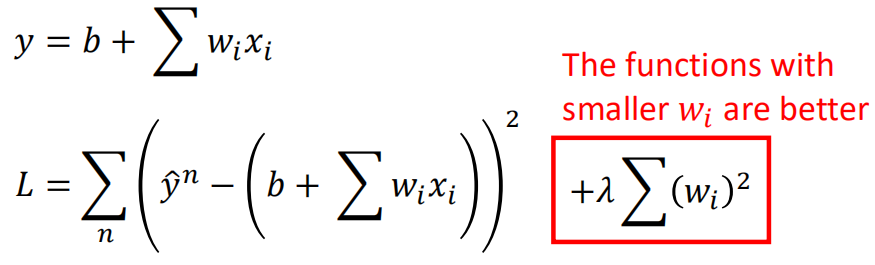
通常wi越小意味着损失也就越小，结果就越好，前面提到正则项通常解释为先验知识，因为在实际情况中，我们认为曲线越光滑则越接近于实际情况，这里的wi就是用来约束拟合结果的光滑程度，拟合结果可以写作：
上式可以看出，更小的wi可以使得曲线变得光滑，但也不能过于光滑。从正则化项来看，λ和w二者是呈反比的，即λ越大，则w就越小，就越光滑，当λ的值很小时，其惩罚项值不大，还是会出现过拟合现象，当时λ的值逐渐调大的时候，过拟合现象的程度越来越低，但是当λ的值超过一个阈值时，就会出现欠拟合现象，因为其惩罚项太大，导致w过小，从而丢失太多的特征，甚至一些比较重要的特征。
那么实际对上面最后一个模型进行训练时，选取不同λ跟误差的关系如图所示:
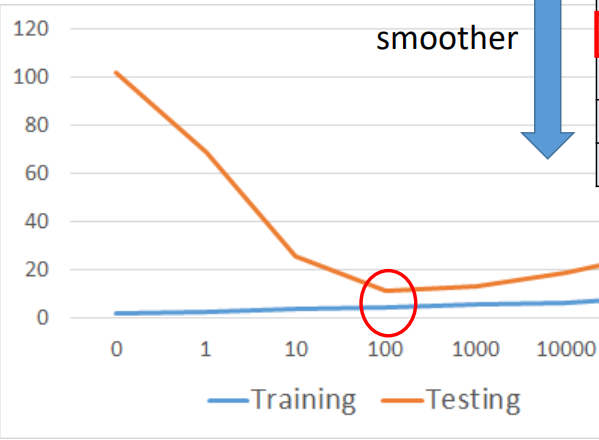
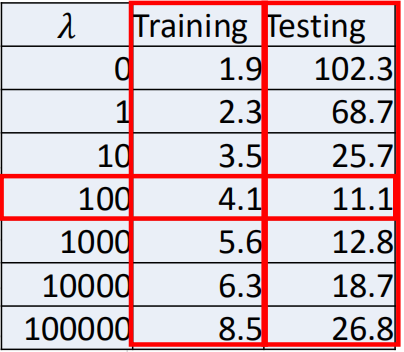
关于误差
前面说到误差是样本的真实值与预测之间差值，其包含了两部分：偏差和方差，可以想象为打靶，偏差表示偏离靶心的程度，偏离靶心越大说明偏差就越大；而方差表示打靶时所打的那些点的散乱程度，越散乱表示方差越大，如下一张图可以很好地说明二者的关系：
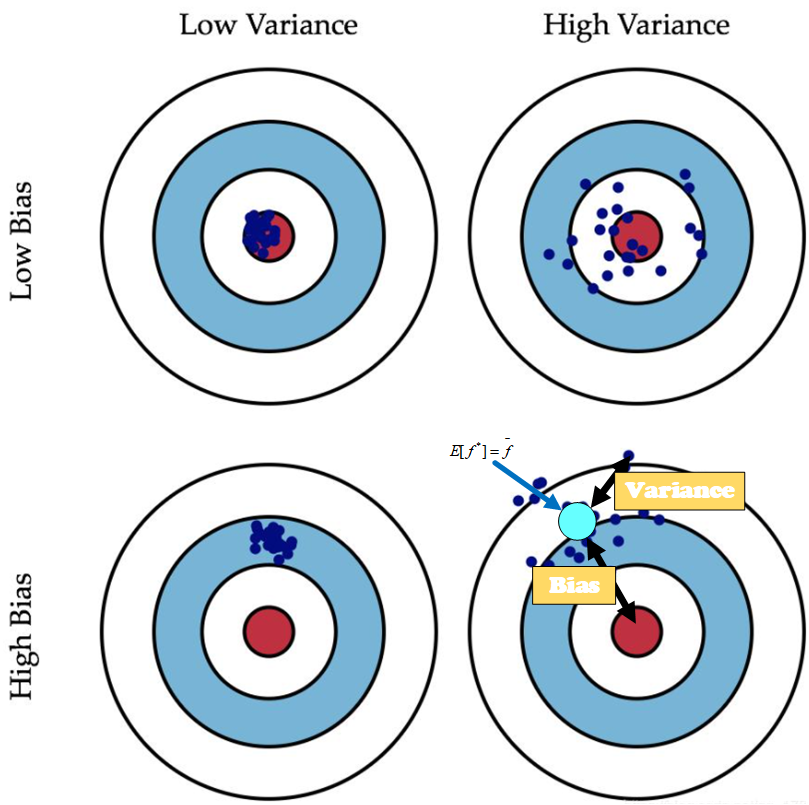
对比于打靶，在模型训练过程中，偏差表示模型对数据集的拟合程度，即样本真实值与预测值之间的偏差，即模型本身的拟合能力，偏差越小说明模型对训练数据拟合的越好，而方差则表示模型的泛化能力，越小的方差表示模型的泛化能力越强。
举例说明：
现有500个样本，每组样本有10个，共500组，现用不同的复杂程度的模型对500组样本分别进行拟合，得若干组含有500组不同的参数和模型，将其画在一张图上：
方差部分：
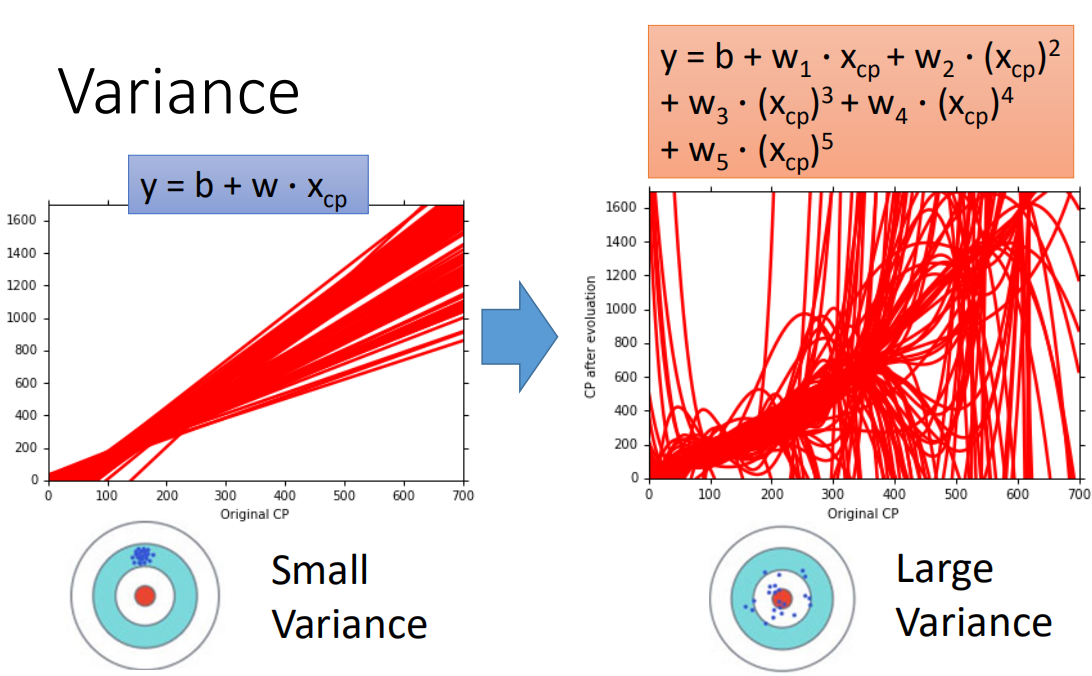
可以看到，简单模型拥有更小的方差，都集中在一起，而当模型变得复杂后，及其散乱，方差变大；同样，对比不用复杂程度模型的偏差：
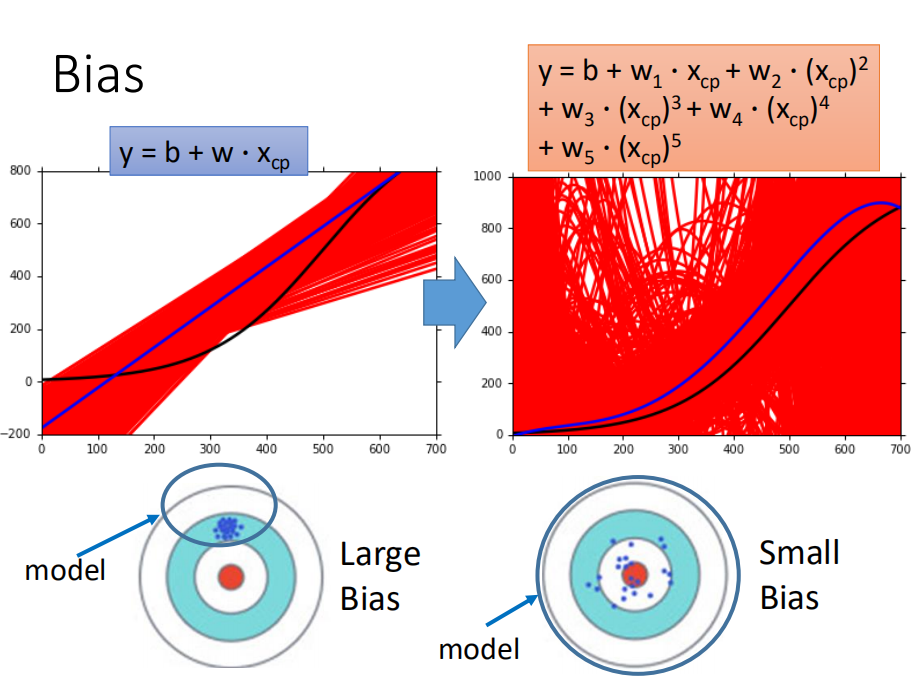
可以看到模型过于简单，对数据的拟合不足，具有较大的偏差，而复杂的模型能够更好的拟合数据。
模型偏差、方差随着模型复杂度变化如图：
可以看出，当模型较为简单时，偏差大，方差小，而当模型复杂时，偏差减小，方差增大。
当模型在训练样本上具有较大偏差（误差）时，即模型较为简单时，不能很好地拟合数据，我们称之为欠拟合；
当模型在训练样本上具有较小误差，但在测试集上误差很大，说明模型过于复杂，方差较大，这时称之为过拟合（注意，这里两个条件都要满足，不能仅因为在测试集上的误差大就认为是过拟合）。
那么面对欠拟合和过拟合该怎么办呢？
首先是欠拟合，欠拟合的原因是模型过于简单，因此我们可以考虑一下措施：
（1）增加模型复杂程度；
（2）增加更多的特征（其实也是一种增加模型复杂程度）；
（3）减小正则化参数；
对于过拟合，我们考虑模型过于复杂，因此可以：
（1）降低模型复杂程度；
（2）加入正则化；
（3）减少样本特征（也是一种降低模型复杂程度）；
（4）增加训练样本数量（方差的大小与样本数量N有关）；
（5）增大正则化参数；
后面神经网络还有一些其他方法如dropout、earlystopping等。
关于训练
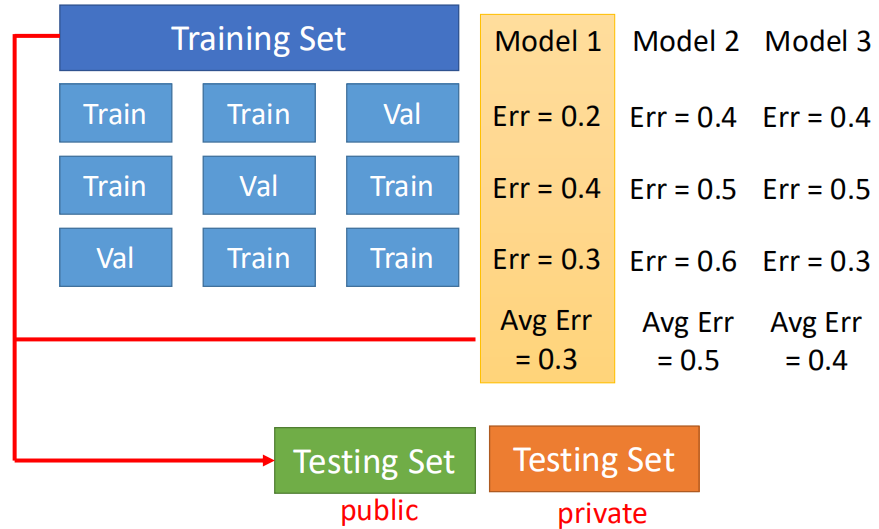
那么再对样本进行训练时，我们一般有训练集和测试集，测试集是为了验证模型好坏的一个数据集，需要是对模型一个陌生的数据集，训练后我们不能直接根据测试集去反过来再去调整模型，这样模型可能会朝着测试集再逐渐优化，使得测试集变成了新的“训练集”，因此训练时我们需要从训练数据中分出一部分数据用户验证模型，称之为验证集，通过验证集调整模型参数，比较著名的就是N-fold cross validation，其做法如下：
新增内容：
2.关于局部加权线性回归
最近看《机器学习实战》一书时，书中提到一种局部加权线性回归算法，这里简单总结一下。
上面线性回归中一开始说到，当利用一个特征时，我们的拟合效果不好，而采用二次方、三次方项的时候，拟合效果较好，而二次方、三次方项相当于我们自己构造出的新的特征。
那么有时我们并不知道或者说要去尝试去构造一些新的特征出来，才能更好的拟合数据，如何能使特征的选择变得不那么重要呢？
同时，如果简单采用一次项的时候，往往很难表示出数据中的一些细节，如下面一个例子：
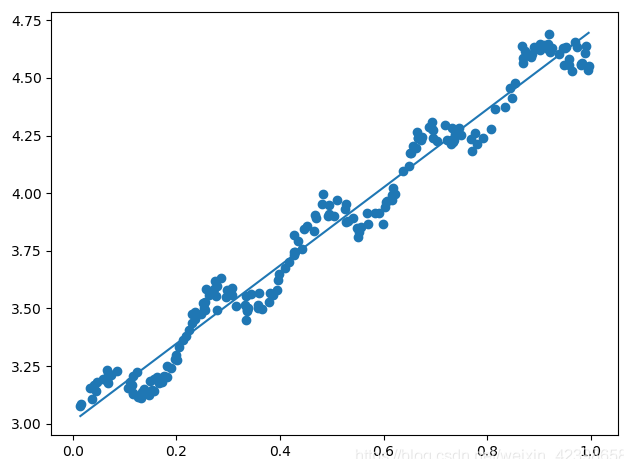
可以看到，如果单纯仅用线性拟合上面一组数据，并不能很好的反映出数据锯齿状的细节。
因此，针对上面两个问题，局部加权线性回归能够解决上面的问题。
所谓局部加权线性回归，是指在进行数据拟合时，对数据赋予一定的权值，使要拟合的点附近的点的权重增大，而离要拟合的点远的数据的权重减小，假设x为要预测的点，x(i)为样本中的某一个点，通常权重的计算方式为：
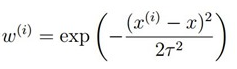
这个是Gaussian RBF核，类似于SVM中引入核函数的概念。其图像如下
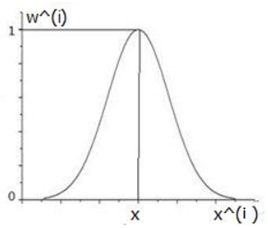
可以看到：
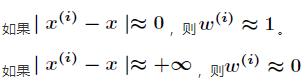
也就是说，距离x较近的点x(i)的权重较大，距离x(i)较远的点的权重较小，甚至消失，式中的τ则控制了权重大小，不同的τ范围不同：
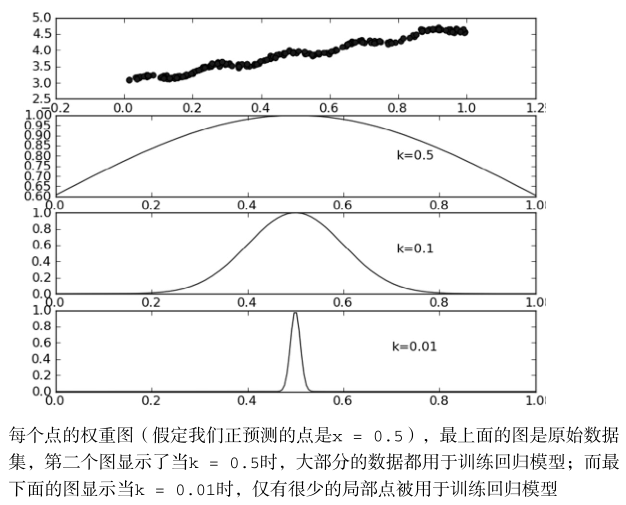
可以看出，τ决定了哪些数据参与到了训练中，但是局部加权也有个缺点，就是在每次进行预测时，都会重新调用整个样本，重新确定参数，因此计算量较大，有点类似KNN。
这种方法通过OLE方法求解，方法如下：
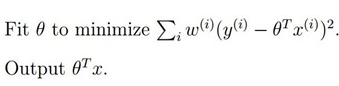
下面看一下实现过程：
# 局部线性回归 def lwlr(testPoint, xArr, yArr, k=1.0): xMat = np.mat(xArr) yMat = np.mat(yArr).T m = np.shape(xMat)[0] # 取矩阵的行数 weights = np.mat(np.eye((m))) # 创建一个对角矩阵，对角线为1，其他为0 for j in range(m): #next 2 lines create weights matrix diffMat = testPoint - xMat[j,:] # 开始计算权值了 weights[j,j] = np.exp(diffMat*diffMat.T/(-2.0*k**2)) xTx = xMat.T * (weights * xMat) if np.linalg.det(xTx) == 0.0: print("矩阵不可逆") return ws = xTx.I * (xMat.T * (weights * yMat)) return testPoint * ws def lwlrTest(testArr,xArr,yArr,k=1.0): #loops over all the data points and applies lwlr to each one m = np.shape(testArr)[0] yHat = np.zeros(m) for i in range(m): yHat[i] = lwlr(testArr[i],xArr,yArr,k) return yHat
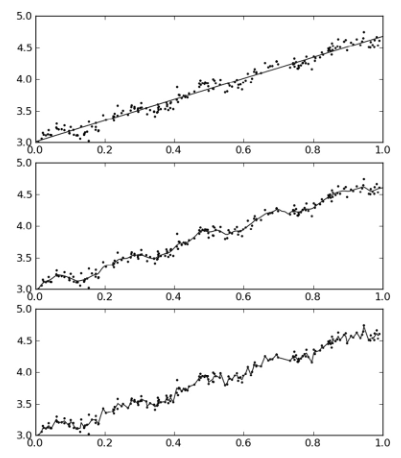
测试数据如图所示：
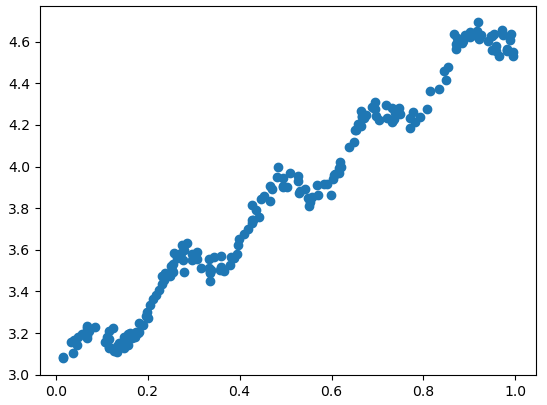
测试代码一下上面的两个函数：
x, y = loadDataSet('./ex0.txt') fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.scatter(mat(x)[:, 1].flatten().A[0], mat(y).T[:, 0].flatten().A[0]) yHat = lwlrTest(x, x, y, 0.03) srtind = mat(x)[:, 1].argsort(0) xsort = mat(x)[srtind][:, 0, :] ax.plot(xsort[:, 1], yHat[srtind], 'red', linewidth=2)
看下效果：
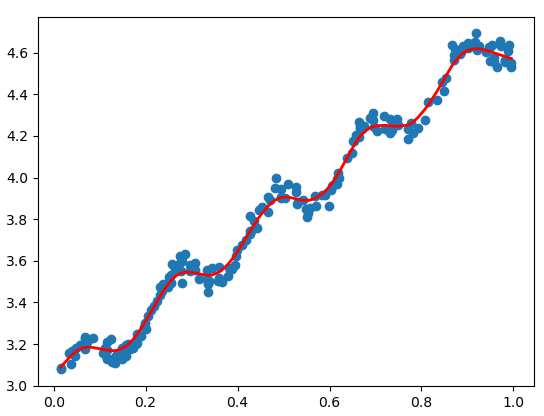
可以看到，这样的拟合按照数据的“纹路”进行拟合了，就相当于是每次只对于每一小部分数据进行拟合。
加权加权回归是一种非参数回归，因为其每次预测都需要重新计算一遍参数，且每次参数都不一样，没有固定的参数，所以称之为非参数模型。
上面就是局部加权线性回归了，由于其主要是采用的是最小二乘的解析解形式，所以前面没有说到这一部分内容，这里做一个补充，后面还有所谓的L1正则和L2正则对应的岭回归和Lasso回归，后面进一步补充。
有关线性回归的内容到这里就基本结束了，其中很多问题在回顾的过程中会有更深刻的理解，由于线性回归属于机器学习入门，其实现比较简单就不作讨论了，值得一提的是，线性回归还有另外一种正规方程解法，对应的sklearn库中的LinearRegressin的API，本文的梯度下降求解方法则对应着SGDRegressor的API，二者是有区别的。
