【Python机器学习实战】感知机和支持向量机学习笔记(二)
上文主要对感知机和SVM进行了简要概括,并对感知机和SVM利用梯度下降算法求解的过程,这篇主要对SVM的对偶形式转化及求解过程进行学习。
SVM的对偶形式
理论上对于线性可分的数据,采用梯度下降对SVM进行求解和学习已能满足基本要求,但考虑到非线性数据,以及问题求解的复杂程度等问题,将SVM原始问题转化为其对偶形式能够更好地解决问题,因此转化为对偶形式是必要的,总结下来,转化为对偶形式有以下好处:
- 转化为对偶形式后,原始问题中的不等式约束将变为等式约束,便于求解;
- 对偶问题降低了求解的复杂度,原始问题中求解w转化为对偶问题中的α,原始问题中的w与样本的特征数量有关,当数据维度过大时,求解复杂度变高,而α的求解仅与样本的数量有关;
- 求解速度更快,当求解α时,当样本为非支持向量时,α的值为0,只有当样本为支持向量时,对应的α才为非零;
- 对偶问题方便运用核方法解决非线性问题,引入核函数变得简单
下面就简要介绍下SVM的对偶形式的转化过程:
SVM对偶形式的转化过程:
根据上一节中,硬间隔SVM的目标函数(后边会说软间隔):
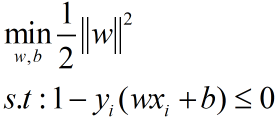
引入拉格朗日乘子:
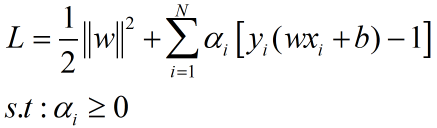
分别对w,b进行求导,并令其为0,运算得:
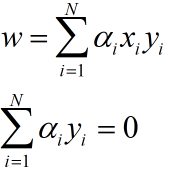
将其代入回拉格朗日乘子目标函数并运算(运算过程略),可得:
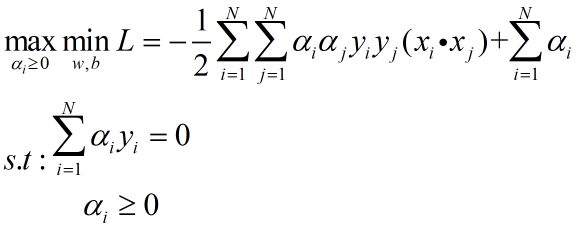
对于软间隔SVM而言,其结果与硬间隔一直,差别就在于约束条件不同,下面给出软间隔SVM的对偶形式:
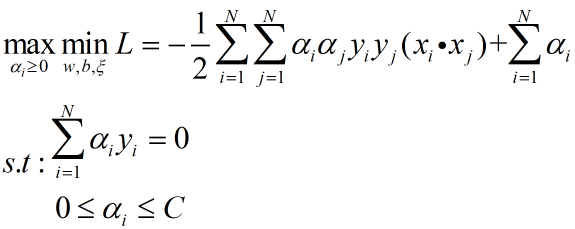
接下来就是对SVM的对偶形式进行求解,只要求得了α*即可同步求得w*和b*,即:
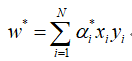
 至于如何求解α*后文再进一步详细展开,在求解α*之前先对支持向量进行解释,首先描述支持向量,假设支持向量集合用SV表示,那么:
至于如何求解α*后文再进一步详细展开,在求解α*之前先对支持向量进行解释,首先描述支持向量,假设支持向量集合用SV表示,那么:
-
- 在硬间隔中对任意xi∈SV<=>αi>0;
- 在软间隔中任意xi∈SV<=>0<αi≤C;
由于在软间隔对偶形式中已对αi进行了αi≤C限制,因此这里统一为:统一为对任意xi∈SV<=>αi>0。
这里进一步说明一下,按照KKT条件,根据αi、ξi是如何确定分离边界和分离超平面之间的位置关系呢?具体而言:
-
- 当αi=0时,此时样本xi被正确分类,样本点可能落在分离边界上也可能不落在分离边界上,xi不是支持向量;
- 当0<αi<C时,样本xi被正确分类,且xi是支持向量;
- 当αi=C时:
- ξi=0时,样本xi被正确分类,样本落在分离边界上,且为支持向量;
- 0<ξi<1时,样本xi被正确分类,样本落在分离边界和分离超平面之间;
- ξi=1时,样本刚好落在分离超平面上;
- ξi>1时,样本xi被错误分类。
接下来就是求解α*的问题,目前有很多较为成熟的算法,而其中最著名的算法为SMO算法,其主要思想是在循环中选取两个变量,其余视为定值,不断构建二次规划问题,对二次函数优化问题进行求解。具体而言:
- 目标函数及其约束条件为:
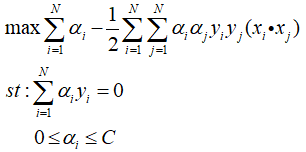
- 对于参数(α1,α2,...,αN)所对应的样本点x1~xN,考察各个样本的KKT情况;
- 若所有样本的KKT情况都在容许误差范围内,则训练完毕,否则选取违反KKT最严重的样本点,作为第一变量;
- 然后选取除第一变量以外的其它的另一个变量作为第二变量,选取方法是个复杂高效的过程,但就实际应用而言,通常采用随机的方法;
- 然后对两个选取的变量进行更新,根据更新后的两个变量更新预测值y,重复上述步骤即可(在后文中引入核函数后,一并会详细说明该步骤)。
上述即为SMO算法的简要步骤,上面提到了KKT条件,样本点xi对应的KKT条件为:
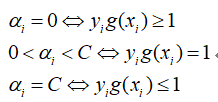
所谓违反KKT条件最严重的样本点,这里介绍一种较为快捷有效的方法:
-
- 计算样本的损失变量c,c的定义如下:

-
- 将c复制三份,分别为c(1),c(2),c(3),并分情况计算对应位置的损失情况,具体来说:
- 将αi>0或yig(xi)>1所对应的位置的ci(1)置为0;
- 将αi=0或yig(xi)=1所对应的位置的ci(2)置为0;
- 将αi<00或yig(xi)<1所对应的位置的ci(1)置为0
- 然后将c(1),c(2),c(3)相加,取出损失向量中值最大的一项的下标i,该下标对应的αi作为第一变量,即:
- 将c复制三份,分别为c(1),c(2),c(3),并分情况计算对应位置的损失情况,具体来说:
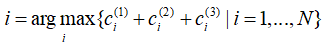
上述就是SMO算法的大致步骤,仅说明了参数选取的规则和方法,具体优化求解和迭代到后文中引入核函数后,一并进行解释。
核函数的引入
当数据在低维空间线性不可分时,我们希望将其映射到高维空间变成线性可分的,如下图。因此,需要寻找一个映射φ将数据从低维空间映射到高维空间。Cover定理证明了当空间维数越大时,数据线性可分的概率越大。然而在应用过程中寻找一个映射将数据从低维到高维空间变得线性可分的难度高于问题本身,核技巧恰巧为解决这样的问题提供了便利。
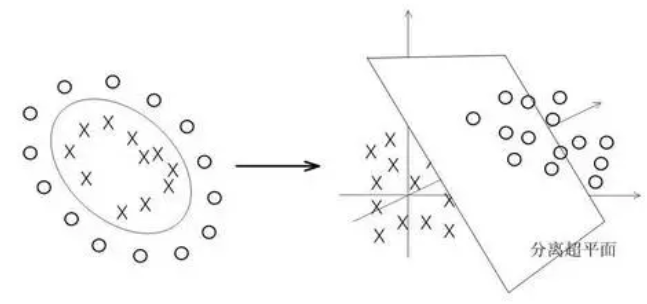
核技巧不同于核方法,核技巧更注重应用,核技巧并不注重去寻找这样一个映射,而是将这个映射的过程再次进行转化,使得映射函数φ变得不再显式表示,从而使问题变得简单。简单来说,核技巧就是利用核函数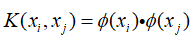 来替代式中出现的内积(xi·xj),核技巧的基本思想如下:
来替代式中出现的内积(xi·xj),核技巧的基本思想如下:
-
- 将算法表述成样本点的内积的组合;
- 设法找到核函数K(xi,xj),它能返回样本点xi,xj被φ作用后的内积;
- 用K(xi,xj)替代内积(xi·xj),完成样本从低维向高维的映射
注:任意一个损失函数加上一个单调递增的正则化项的优化问题都能利用核技巧(2002 年由 Scholkopf和Smola 证明的定理)
那么如何寻找核函数呢?Mecer定理为核函数的寻找提供了便利,根据其定理可以证明以下函数为核函数:
-
- 多项式核
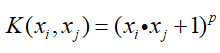
-
- 径向基(RBF)核也叫高斯核
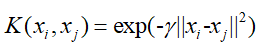
核函数的应用
接下来就是核函数如何进行应用的问题,首先是在感知机中的应用,虽然感知机形式较为简单,此处运用核函数便于后边SVM中核函数的应用。
核感知机的训练过程
感知机中只需将内积替换为核函数即可,核感知机的算法步骤:
-
- 对于训练集D={(x1,y1),(x2,y2),....,(xN,yN)},
- 初始化参数:
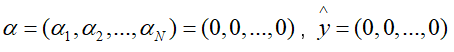
然后计算核矩阵:
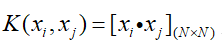
-
- 迭代次数j=1:M,对于误分类样本点集:
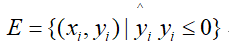
若E为φ,则退出循环,否则选取E中任一个误分类的点对参数进行更新,更新过程为:
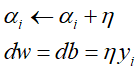
-
- 利用dw和db对y进行预测:
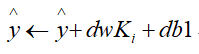
其中K•为K的第i行,1表示全为1的向量。
-
- 最终输出模型为:
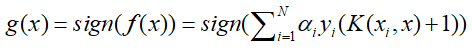
核SVM的训练过程
接下来是核SVM的训练过程,该过程也是将对偶形式中的内积形式替换为核函数即可,替换后的目标函数变为:
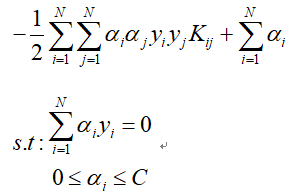
不妨设α1,α2为选定的两个变量,其余均为固定值,那么上述目标函数变为:
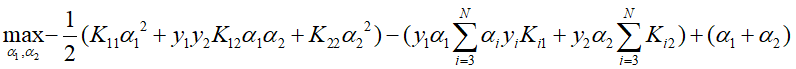
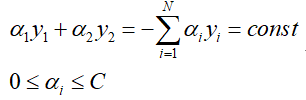 其中const为常数,从而问题转化为 对二次函数求极值的问题。前文已经讲述了SMO算法中如何选取变量的过程,具体训练步骤:
其中const为常数,从而问题转化为 对二次函数求极值的问题。前文已经讲述了SMO算法中如何选取变量的过程,具体训练步骤:
-
- 初始化参数,并计算核矩阵:
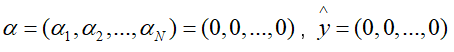
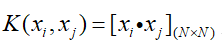
-
- 对于迭代次数j=1:M,考察样本违反KKT条件情况,选出违反KKT条件最严重的样本(上文已进行叙述),若其在容忍阈值ε内,则退出循环,否则将该样本对应下标的α作为第一变量,作为α1,随机选取第二变量α2(选取方法上文已说明)。
- 根据选取的两个参数开始进行更新,首先更新α2,它由以下几个参数定出:
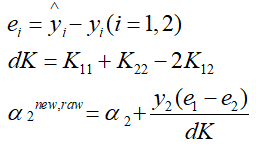
注:α2的求解可以根据上述目标函数求解出来,即将α1用α2表示,然后带回,求解一元二次函数的最大值,结果即为上式(推导过程略)。
-
- 然后根据约束条件,重新确定α2的上下界:
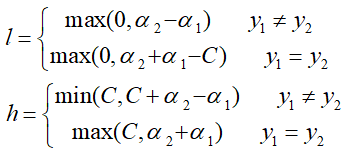
-
- 根据上下界,对α2的值进行裁剪:
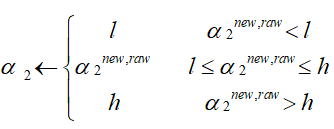
-
- 这里要记录下α2的增量用于更新α1,即:
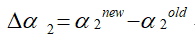
-
- 然后根据该增量求出新的α1,即:

-
- 利用α1和α2对局部参数进行更新,分别求出dw和db:
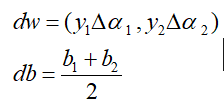
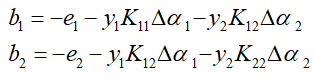
-
- 然后根据dw和db更新预测值y:
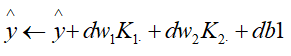
至此一次迭代完成,返回至第二步。
-
- 输出训练模型:
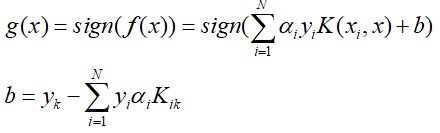 其中k满足:
其中k满足:
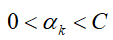
可以证明这样的k必然存在,证明从略。
至此,感知机和支持向量机算法已大致进行了简要介绍。考虑到感知机较为简单,且较少单独用来模型训练,不作实现过程,后面进一步支持向量机算法进行实现,进一步加深对算法的理解,然后找一些数据集,利用sklearn实现SVM算法。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构