密度聚类
聚类算法可以划分为三大类，第一类是kmeans、DBSCAN、Density Peaks 依据密度的聚类方式；第二类是类似于层次聚类的依据树状结构的聚类方式；第三类是谱聚类，依据图谱结构的聚类方式.。
DBSCAN
DBSCAN是一种密度聚类，他不要求指定聚类中心数量，能够避免异常值，对非球形的形状也可以聚起来，这些都是kmeans做不到的。DBSCAN依赖两个参数进行聚类：
$\varepsilon $ 半径。用于扩展簇时的搜索半径范围
minPts 最小点。用于扩展簇时判定是否将点纳入簇内
算法的流程如下
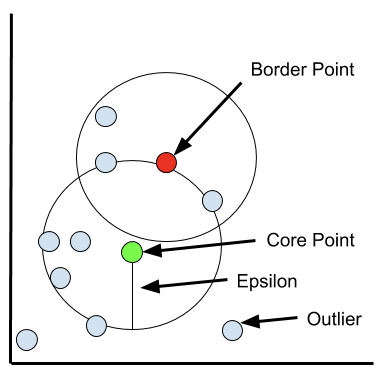
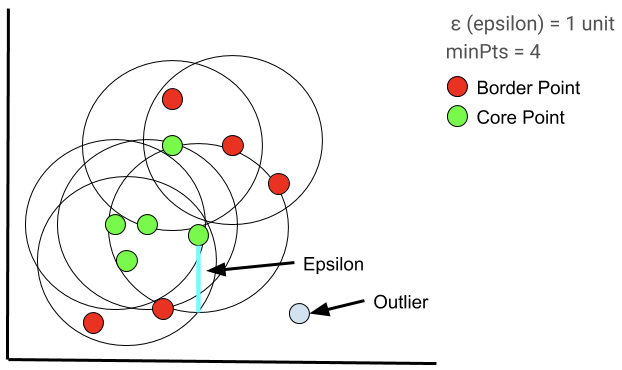
- 初始化：选取一个点，要求该点在$\varepsilon $ 半径范围内拥有至少minPts个点（包括该点本身），这个点被记为核心点
- 遍历在核心点半径内的其他点。如果其他点的$\varepsilon $ 半径范围内，同样具有至少minPts个点，那么同样记该点为核心点；如果这个点半径内没有minPts个点，则记这个点为边界点。
- 重复第2步，直到选完所有核心点和边界点
如何确定最优$\varepsilon $？用不同的$\varepsilon $计算每个点到半径内邻居的平均距离，将他们画在图上，y轴表示平均距离，x轴表示半径，用手肘法，找到手肘的位置，则为$\varepsilon $的合适取值
如何确定最优minPts？通常设置minPts为数据的维度的1到2倍。
Density Peaks
Density Peaks 又叫峰值密度聚类，局部密度聚类。它的聚类基于两点假设：1、簇中心的局部密度要大于围绕他的点的局部密度。2、不同簇中心距离较远。
$\rho_{i}$ 局部密度。给定$d_{ij}$表示ij两点之间的距离，设置超参数$d_{c}$，点i的局部密度$\rho_{i}$，是所有$d_{ij}<d_{c}$ 的点的个数。
$\delta_{i}$ 聚类中心距离。确定每个点的聚类中心距离，分为两种情况：
- 密度最大的点的聚类中心距离，等于距离i点最远的点n的直线距离$d_{in}$。
- 其他点的中心距离，等于所有密度大于自身的点中，距离最近的点的直线距离。
- 最后需要做归一化处理，距离最大的点（也就是密度最大的点），它的距离定为1
当有了$\rho_{i}$ 和 $\delta_{i}$ 后，将密度和距离分别作为横轴和纵轴绘制出二维决策图
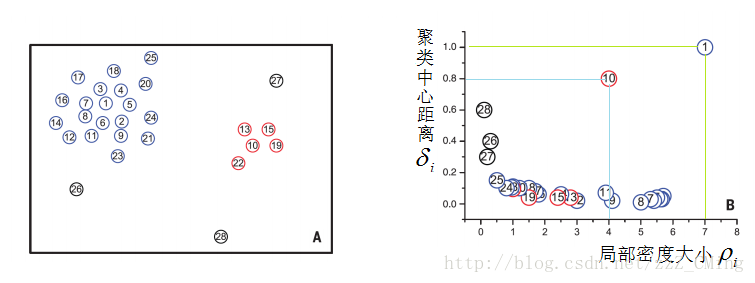
看右侧的图，右上角区域的是聚类的核心点，它的密度大，且距离其他的核心点比较远。右下角虽然密度大，但是周围也有很多密度大的点，距离比较近，不适合做聚类中心。左上角的点密度小，距离其他点也远，属于孤立点，不适合做聚类中心。
应用中，可以用$\rho_{i} * \delta_{i}$ 排序，选取前K个点作为中心点。
