从Bellman方程到派单算法（二）-- MDP的求解方法DP、MC和TD

DP、MC和TD

动态规划、蒙特卡罗和时序差分是求解贝尔曼方程的方法。不得不说，这三个名字无论是汉字还是英文缩写，都体现着王霸之气，一看就是不好惹的家伙，甚至它还没出手，你就倒下了。但是如果抛开证明不谈，只求学个整体的概念，看到这个名字的时候知道是怎么回事儿，这东西怎么用，那以大多数人的功力来说还是可以一战的。

 

贝尔曼方程和最优解

 

 

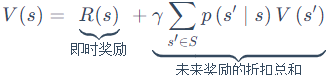
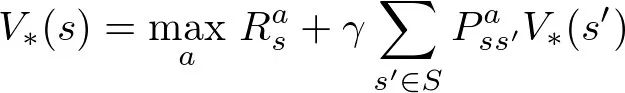
三种方法的图解

 

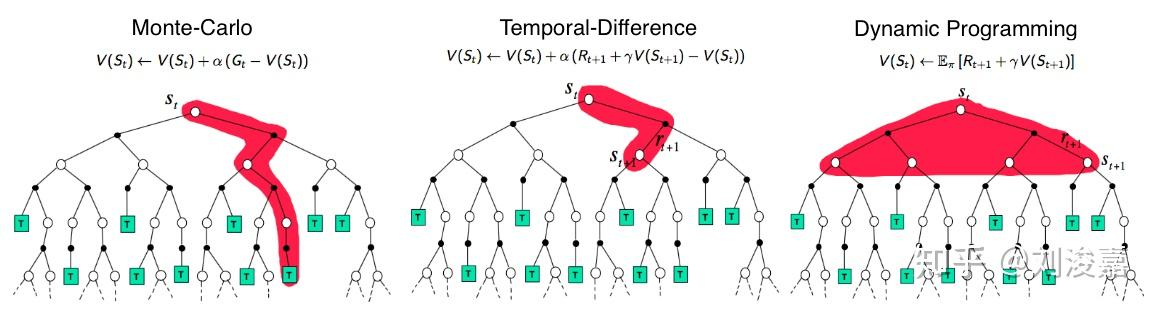
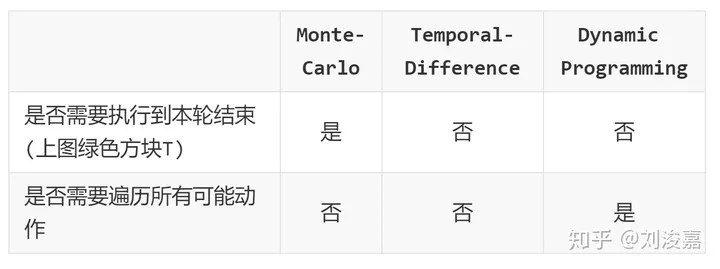
三种方法的特点

 

动态规划

动态规划我们知道，它具有最优子结构和无后向型。也就是说当前状态的下的价值函数，可以用下一状态的价值函数来计算。所以每一个状态的最优值函数（贝尔曼最优解），可以用下一个状态的最优值函数与即时回报来表示：

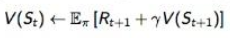
这里的期望指的是在策略π下，所有的行动a带来的即时回报与下一个状态的收益。这里就出现了问题，不同的策略π(a|s)，他们在s下采用行动a的概率就不一样，得到的期望也就不一样，那么最优值函数还要考虑到所有策略，选出最优策略来，再对最优值函数进行求解。这种思想对应的方法叫做策略迭代，即：假设我们有一个策略π，那么我们可以用策略估计获得它的值函数V^π(s)，然后根据策略改进得到更好的策略π'，接着再计算V^π'(s),再获得更好的策略π'' ... 这样的计算方式效率不高，所以一般回不考虑最优策略是什么，直接看最优值，该方法叫做值迭代。在值迭代的第k+1次迭代时，直接将能获得的最大的V^π(s)值赋给V_k+1（不管什么策略，只看那个能带来最大的V的行动就行）。 可以人为设置数值，当一次迭代所更新的值小于δ时，停止更新。

值迭代算法直接用可能转到的下一步s'的V(s')来更新当前的V(s)，算法甚至都不需要存储策略π。而实际上这种更新方式同时却改变了策略π_k和V(s)的估值V_k(s)。 直到算法结束后，我们再通过V值来获得最优的π。

动态规划的优点在于它有很好的数学上的解释，但是动态要求一个完全已知的环境模型，这在现实中是很难做到的。另外，当状态数量较大的时候，动态规划法的效率也将是一个问题。

 

蒙特卡罗

蒙特卡罗方法是一个采样统计的方法，简单来说就是做随机实验，当实验次数越多，实验结果就越接近其概率值。这个方法对比动态规划来说，他可以不用知道环境是什么，只要做实验，看结果就行。但是他的局限性也在于，每次实验必须要有个结果，也就是说，需要在有限步内达到终止状态获得最终回报。

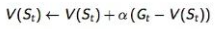
从公式看，MC就是迭代地让V(s)趋近于G_t，这里的G_t表示最终回报，是从当前状态到达最终状态能获得的回报总和。

具体方法是，在初始状态s，遵循策略π，最终获得了总回报R。选取很多这样的样本，得到特定策略π对应的V^π和Q^π，然后进行策略改进，最终形成策略迭代。

1、策略估计，计算V^π(s)。V^π(s)是这些样本中所有到达s的样本，从s到最终状态的的累计回报的均值。

2、策略迭代。在状态转移概率p(s'|a,s)已知的情况下，策略估计后有了新的值函数，我们就可以进行策略改进了，只需要看哪个动作能获得最大的期望累积回报就可以。但是门特卡罗方法是不知道转移概率的（因为环境不可知）。为此，我们需要估计动作值函数Q^π(s,a)。Q^π(s,a)的估计方法前面类似，即在状态s下采用动作a，后续遵循策略π获得的期望累积回报即为Q^π(s,a)，依然用平均回报来估计它。有了Q值，再更新策略 π'(s) = argmax Q^π(s, a)。

3、如果一直选取Q最大的动作a，那么会导致一些还没探索到的a没有机会被选取，即Q不一定是最优的，基于此，一般都用软性策略（soft policies），如ε-greedy policy，在所有的状态下，用1-ε的概率来执行当前的最优动作，ε的概率来执行其他动作，这样可以获得所有动作的预估值，然后慢慢减少ε，使算法收敛。

但就像DP中，如果找到最优的Q，则需要无穷多的episode（环境不可知，不知道转移概率，也就不知道最优的Q），所以在DP中有值迭代的做法，再蒙特卡罗中也有类似的trick，叫做广义策略迭代，即每次迭代策略时，Q不一定找到所有Q里最大的去更新，而是可以在当前episode中找最大的Q去更新π，并最终收敛到最优策略。

 

时序差分

时序差分算法结合了DP和MC的优点，舍弃了缺点，不需要环境模型，不局限于episode task，可以用于连续的任务。

回想蒙特卡罗的公式，如果将

$V(s) = V(s) + \alpha  (G_{t} - V(s_{t}))$

改为

$V(s) = V(s) + \alpha  (R_{t+1} + \gamma (V(s_{t+1})) - V(s_{t}))$

上式即为TD方法。比起MC方法，TD把需要走到终点状态的最终回报，变成了走到下一步的及时回报和下一步的价值。这样就避免了一定要走到一个最终状态，可以应用在连续任务中；也避免了状态转移概率，类似MC，通过多次试验来逼近真值。

伪代码：

 

 

参考

https://www.cnblogs.com/jinxulin/p/5116332.html

https://datawhalechina.github.io/easy-rl/#/chapter2/chapter2?id=_233-%e9%a9%ac%e5%b0%94%e5%8f%af%e5%a4%ab%e5%86%b3%e7%ad%96%e8%bf%87%e7%a8%8b%e4%b8%ad%e7%9a%84%e4%bb%b7%e5%80%bc%e5%87%bd%e6%95%b0

https://zhuanlan.zhihu.com/p/114482584