从Bellman方程到派单算法（三）-- 派单算法
在派单决策中的MDP
MDP构建
在派单决策中，构建MDP来表示不同时空下的价值，并应用到线上派单中。以司机为智能体，有：
S：时间和空间预先划分为时间片和六边形区域，每一个(时间片-六边形)表示一个状态
A：两种动作：接单和空闲。
P：接单会100%概率转移到状态(完单时间片，终点六边形)，不接单会100%概率转移到状态(下一个时间片，此六边形)。
R：接单会收获订单价值，不接单则收获0。R由系统的优化目标决定，一般来说，目标设为最大GMV，则R可定义为订单金额。
γ：折扣因子表示着未来的状态能够多大程度影响到现在的收益。这里有一个分歧，折扣因子可以理解为对未来的不确定性，而我们的历史数据，无论是回报（订单金额），还是时间（送驾时间），都已经是确定的值了，所以收益并不会随着时间的增加而降低。论文中用的
来表示收益，而实践中，我们将这里的γ定为了1。
Learning
这一步利用离线数据，在线下学习每一个时空分布的状态价值，该价值就表示司机在在此状态下直到过程结束的未来的收益。
用时序差分TD定义了迭代公式：
空闲的：
， 
接单的：
，
这里用了动态规划DP做计算，我们只计算司机在一天内的过程。在实践中，为了最小化跨日期的订单带来的影响，我们将一天的切分时间定在了凌晨4点。
此处的γ△t(ai)和计算Rγ中的γ不同，前者设置为0.95，后者设为1。
关于时序差分和动态规划的解法，可以见https://www.cnblogs.com/4PrivetDrive/p/17623650.html
Planning
这一步设置线上的目标函数和约束项
找到最大化行动价值的每个司机的行动策略，并在一个司机只能接一单，一单只能被一个司机接的约束下求解。
由此可以将问题建模为二分图，司机和订单节点之间的权重用该行动的行为价值Qπ(i,j)表示。
优势函数简化Planning
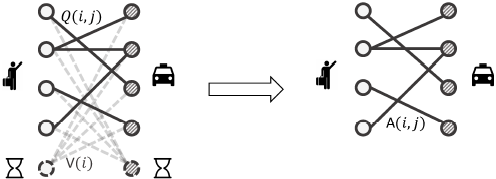
在二部图中，司机可以不接订单，什么都不做，这样的司机和订单之间也会有连线，这个二部图是一个完全二部图。为了减少计算的复杂度，采用了优势函数进行简化计算。
- 在实时计算中，由于派单的间隔很短（1s-3s），这个量级比上状态的时间（10min）是非常小的，所以可以认为当司机采取不接单的动作时，状态价值不会改变，所以司机不接单，他的动作价值就等于该司机当前的状态价值：Qπ(i,0) = V(i)
- 对于优势函数
来说，不接单相当于A=0。把二部图的权重转换为优势函数A，可以在二部图中删除权重为0的连线。（优势函数Aπ(s,a)>0说明行为a的价值大于平均值，应当鼓励，反之则应当避免）
一番操作之后，可以将二部图从左边变为右边的形式，注意权重的定义的改变，目标函数和约束项也随之改变
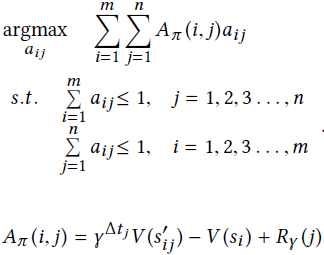
取消率
论文中没有提及取消率，实际上取消率是隐含在Q函数里面的。把下式的Q(s, a)拆开可以看到
这里的P表示订单的取消率。因为在现实情况下，给订单指派司机，有可能会被渠道PK取消和司乘派后取消，所以在行动 a=接单 的情况下，状态s会有两种转移的可能性：订单被取消，还是状态s不变；订单完单，则转移到状态s'，s'是订单完单的时间片和订单的终点六边形所在的状态。所以定义P为订单取消的概率，简称取消率。
正因为取消率P的存在，行动a的即时收益应该为订单价格的期望，所以R=(1-P)*price
取消率用二分类模型做预测，注意的是取消率说的是司乘对的取消率，考虑到订单和司机两方面因素，还要考虑到渠道因素等特征。
isotonic regression
对模型进行校准是因为我们希望模型给出的预测概率能反映真实的取消率。预测取消率用的模型是xgboost，需要进行校准。
isotonic regression又叫保序回归，是一种校准算法，主要思想是通过不断合并、调整违反单调性的局部区间，使得最终得到的区间满足单调性。他的优点是在数据集大的时候效果更好（否则容易过拟合）、不用训练、且调整之后排序不变（AUC不变）。
对于订单挑司机的情况（一个订单n个司机），看重的是校准后的贴近真实取消率。
对于全局最优的情况（n个订单n个司机），不仅看重校正后贴近真实取消率，还因为由于不同订单可能来自不同渠道，意味着通过不同模型做的预测，希望它们给出的预测具有相同的意义，这样不同渠道之间才有可比性。
网上抄的，不一定对
- 这种boosting decision tree算法，在利用对数损失进行优化模型时，需要校准模型。这是因为预测值大多集中于中间区域，很少预测到接近0或接近1，这也就导致了在给预测值分桶的时候落到首末的桶样本数量少，无法准确地估计概率。
将取消率模型通过isotonic拉齐，派单策略才是完整版，函数f是isotonic模型。
