从Bellman方程到派单算法（一）-- MDP
从MP到MRP再到MDP
MP
M = {S, P}
马尔科夫过程。后续的状态只与当前状态有关，与当前状态之前的状态无关。
MRP
M = {S, P, R, γ}
马尔科夫奖励过程。在马尔科夫过程的基础上增加了奖励R和衰减系数γ<0。
定义Gt为在此时刻到过程结束后所得到的收益。衰减系数体现了时间上的不确定性，离此时刻的状态越远，折扣的越多。
定义v(s)为状态s的价值函数。价值函数是Gt的期望，因为状态s是依照不同的概率转移到下一个状态的，所以不同的状态转移概率乘以对应状态的收益，得到的期望，就是我们要的价值函数。
价值函数可以拆解成如下形式：
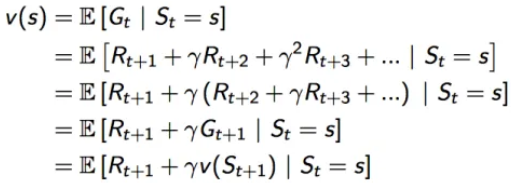
可以看成一个状态的价值 = 即时回报+下一状态的折扣价值。这里的Rt+1可以当做Rt，符号问题不用纠结，就当做即使回报就好。
如果知道了状态转移概率矩阵Pss'，那么期望就可以进一步拆为
如果状态是有限且各个状态的即使回报、状态转移概率都是已知的，那么该式有解析解
MDP
M = {S, A, P, R, γ}
马尔科夫决策过程。在马尔科夫奖励过程的基础上增加了决策过程，也就是行动集A，且这里的P和R都与具体的行为a对应，而不像马尔科夫奖励过程那样仅对应于某个状态，a∈A。
既然引入了行动，必然会涉及到策略，这里用π表示策略(Policy)。含义是在状态s下，采取各个行动a的概率，记为π(a|s)。
马尔科夫奖励过程(MRP)，在执行策略π时，有如下的状态转移概率和奖励函数
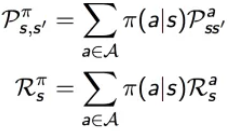
由于行动a的加入，定义行为价值函数，记为qπ(s,a)，表示在执行策略π时，对当前状态s执行某一具体行为a所能得到的收益的期望，也就是在状态s执行a的价值。
我们知道，状态s，采取了行动a，转移到了状态s'，这其中的状态价值可以通过全部的行为价值求和计算得到，而行为价值，也可以通过全部的状态价值求和计算得到，可以写出以下公式
该状态的价值，等于该状态能采取的动作的动作价值之和
该动作的价值，等于该动作带来的即时收益，加上在该动作的作用下，能够转移到的所有的下一个状态的状态价值之和
将公式互相带入，可以得到迭代式
放两个图帮助理解
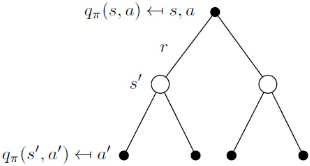
同样的，类似MRP里讲的，vπ(s)是有解析解的 
Bellman方程
Bellman方程用于求解马尔科夫决策过程（MDP）。 Bellman方程是一个递归方程，可以用动态规划求解，通过求解该方程可以找到最优值函数和最优策略。
其实上面已经将贝尔曼方程解释过了，他就是将优化问题迭代的变成了子问题，通过寻找下一阶段的子问题的最优解来解决这一个子问题的最优解。
最优值函数V*的求解公式如下：
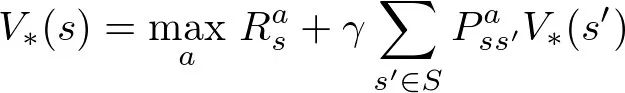
对于每个MDP，总有至少一个策略优于或等于所有其他策略。如上图的公式，V(s) = f(V(s))，MDP一定有一个最优解，这个可以用不动点定理证明。
解方程：展开成矩阵的形式
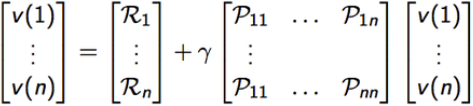
线性方程求解：
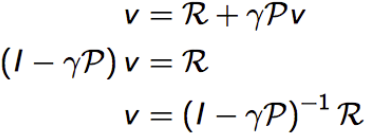
此解法为O(n3)的时间复杂度(为啥我也不知道)，所以一般用一些逐步迭代的算法进行求解，如下：
- 动态规划Dynamic Programming
- 蒙特卡洛评估Monte-Carlo evaluation
- 时序差分学习Temporal-Difference
