L1范数与L2范数

L1范数与L2范数

L1范数

L1范数是指向量中各个元素绝对值之和，也叫“稀疏规则算子”（Lasso regularization）。稀疏的意思是可以让权重矩阵的一部分值等于0，很粗暴。

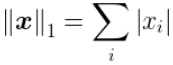
L1范数可以实现稀疏，那么问题来了，实现参数稀疏有什么用？

• 可解释性：可以看到到底是哪些特征和预测的信息有关。
• 特征选择：输入x的大部分特征与输出y是没有关系的，如果让参数矩阵w中出现许多0，则可以直接干掉与y无关的元素，也就是选择出x中真正与y有关的特征。如果不这么做，那么x中本来与y无关的特征也加入到模型中，虽然会更好的减小训练误差，但是在预测新样本的时候会考虑到无关的信息，干扰了预测。

 

L2范数

L2范数是指向量中各元素的的平方和然后再求平方根。有人把它叫“岭回归”（Ridge Regression），有人也叫它“权值衰减weight decay”。

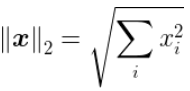
L2范数与L1不同，他不会让参数等于0，而是让每个参数都接近于0。那么L2范数又有什么好处呢？

• 防止过拟合。一般的用法是在损失函数后面加上w的L2范数，即||w||₂​，这是一种规则化。
• 优化求解变得稳定快速。简单地说他可以让w在接近全局最优点w*的时候，还保持着较大的梯度。这样可以跳出局部最优，也使得收敛速度变快。

 

​