sigmoid与softmax
sigmoid与softmax
sigmoid与softmax可以神经网络的输出单元。
原理
sigmoid
预测二值型变量$y$的值,定义如下:
$$\hat{y}= \sigma( \omega^{T}h+b)=\frac{1}{1+exp{-( \omega^ {T}h+b)}}$$
通常使用最大似然来学习,因为最大似然的代价函数是$-log(y|x)$,代价函数中的log抵消了sigmoid中的exp,这样的结果是只有当$\sigma$函数的自变量非常大的时候才会有饱和,也就是梯度变得非常小。
softmax
softmax最常见的多分类器的输出单元。
$$z=W^{T}h+b$$
$$y_{i}=softmax(z_{i})=\frac{exp(z_{i})}{\sum_{j}exp(z_{j})}$$
同样,对数似然中的log可以抵消exp,而其他形式的目标函数(比如平方误差)都不能起到学习的作用。
交叉熵与softmax loss
交叉熵是衡量样本真实分布与样本预测分布的距离,分布距离越小,交叉熵的值就越小,公式如下:
$$H(p,q)=\sum_{i}^{n}-p_{i}log(q_{i})$$
其中$p$是样本真实分布,$q$是预测分布,$n$为样本数量。根据交叉熵的形式,可以写出softmax损失函数公式,$\hat{y_{i}}$是训练数据的真实标签:
$$L=\sum_{i}^{n}-\hat{y_{i}}log(y_{i})$$
softmax的反向传播
链式求导法则可知:
$$\frac{ \partial L}{ \partial z_{i}}=\frac{ \partial L}{ \partial y_{j}} \frac{ \partial y_{j}} {\partial z_{i}}$$
其中$L$对$y_{j}$的导数为:
$$\frac{\partial L}{\partial y_{j}}=\frac{\partial \left[- \sum_{j} \hat{y_{j}}log(y_{j}) \right]}{\partial y_{j}}=- \sum_{j} \frac{\hat{y_{j}}}{y_{j}}$$
$y_{j}$对$z_{i}$的导数要分为两部分看
- $j=i$时:
$$\frac{ \partial y_{j}} {\partial z_{i}}=\frac{ \partial \left[ \frac{e^{z_{i}}}{\sum_{k}e^{z_{k}}}\right]} {\partial z_{i}}$$
$$=\frac { e^{z_{i}} \sum_{k} e^{z_{k}} - (e^{z_{i}})^{2} } { ( \sum_{k} e^{z_{k}} )^{2} }$$
$$=\frac{e^{z_{i}}} {\sum_{k} e^{z_{k}}} (1-\frac{e^{z_{i}}} {\sum_{k} e^{z_{k}}})$$
$$=y_{i}(1-y_{i})$$
- $j \not= i$时:
$$\frac{ \partial y_{j}} {\partial z_{i}}=\frac{ \partial \left[ \frac{e^{z_{i}}}{\sum_{k}e^{z_{k}}}\right]} {\partial z_{i}}$$
$$=\frac{0-e^{z_{j}z_{i}}}{( \sum_{k} e^{z_{k}} )^{2}}$$
$$=-y_{j}y_{i}$$
故
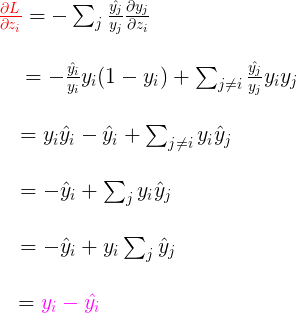



 浙公网安备 33010602011771号
浙公网安备 33010602011771号