POJ2676-Sudoku

【题目描述】

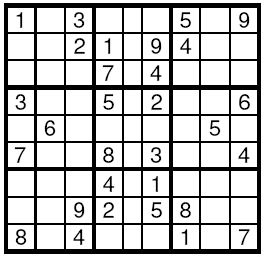
数独是一项非常简单的任务。如图所示，具有9行和9列的方形表被分成9个较小的正方形3x3。在一些单元格中写入从1到9的十进制数字。其他单元格为空。目标是用1到9的十进制数字填充空单元格，每个单元格一个数字，这样在每行，每列和每个标记的3x3子方格中，所有数字从1到9出现。编写程序来解决给定的Sudoku任务。 

【输入】

输入数据将以测试用例的数量开始。对于每个测试用例，后面跟着9行，对应于表的行。在每一行上给出一串精确的9位十进制数字，对应于该行中的单元格。如果单元格为空，则表示为0。

【输出】

对于每个测试用例，您的程序应以与输入数据相同的格式打印解决方案。必须根据规则填充空单元格。如果解决方案不是唯一的，则程序可以打印其中任何一个。

【输入示例】

1

103000509

002109400

000704000

300502006

060000050

700803004

000401000

009205800

804000107

【输出示例】

143628579

572139468

986754231

391542786

468917352

725863914

237481695

619275843

854396127

【思路】

这是一道搜索题，虽然检查的时候很恶心，但是没有什么很难的地方。

因为一共有81个格子，并且题目已经为你填好了一些，所以我们可以从第0个格子开始搜索。

int f(int n)
{
    if(n>80)//如果格子都填满了，跳出，正确。 
    {
        flag=true;
        return 0;
    }
    int i,j;
    if(s[n/9][n%9]!=0)//如果格子已经填了，那么搜索下一个 
        f(n+1);
    else
        for(i=1;i<=9;i++)
            if(check(n,i)==true)
            {
                s[n/9][n%9]=i;
                f(n+1);
                if(flag==true)
                    return 0;
                s[n/9][n%9]=0;//如果不能填，归零。 
            }
}

每一个填的格子有一个检查是否可以应用的函数check

bool check(int n,int x)
{
    int i,j;
    for(i=0;i<9;i++)//横排 
    {
        j=n/9;
        if(s[j][i]==x)
            return false;
    }
    for(i=0;i<9;i++)//竖排 
    {
        j=n%9;
        if(s[i][j]==x)
            return false;
    }
    int a,b;//九宫格判断 
    a=n/9/3*3;
    b=n%9/3*3; 
    for(i=a;i<a+3;i++)
        for(j=b;j<b+3;j++)
        {
            if(s[i][j]==x)
                return false;
        }
    return true;
}

最重要的一点是每次输完一个数据之后要清零。我就因为这个改了很久。

#include<iostream>
using namespace std;
bool flag=false;
int s[15][15];
void in()
{
    char sd[15][15];
    int i,j;
    for(i=0;i<9;i++)
        for(j=0;j<9;j++)
        {
            cin>>sd[i][j];
            s[i][j]=sd[i][j]-'0';
        }
}
void out()
{
    int i,j;
    for(i=0;i<9;i++)
    {
        for(j=0;j<9;j++)
            cout<<s[i][j];
        cout<<endl;
    }
}
bool check(int n,int x)
{
    int i,j;
    for(i=0;i<9;i++)//横排 
    {
        j=n/9;
        if(s[j][i]==x)
            return false;
    }
    for(i=0;i<9;i++)//竖排 
    {
        j=n%9;
        if(s[i][j]==x)
            return false;
    }
    int a,b;//九宫格判断 
    a=n/9/3*3;
    b=n%9/3*3; 
    for(i=a;i<a+3;i++)
        for(j=b;j<b+3;j++)
        {
            if(s[i][j]==x)
                return false;
        }
    return true;
}
int f(int n)
{
    if(n>80)//如果格子都填满了，跳出，正确。 
    {
        flag=true;
        return 0;
    }
    int i,j;
    if(s[n/9][n%9]!=0)//如果格子已经填了，那么搜索下一个 
        f(n+1);
    else
        for(i=1;i<=9;i++)
            if(check(n,i)==true)
            {
                s[n/9][n%9]=i;
                f(n+1);
                if(flag==true)
                    return 0;
                s[n/9][n%9]=0;//如果不能填，归零。 
            }
}
int main()
{
    int m;
    cin>>m;
    int i,j;
    for(i=0;i<m;i++)
    {
        in();
        f(0);
        out();
        flag=false;
    }
    return 0;
}