最小二乘法-多项式拟合曲线

　　如果你有一批散点图，像以下，（图都是从百度找的）

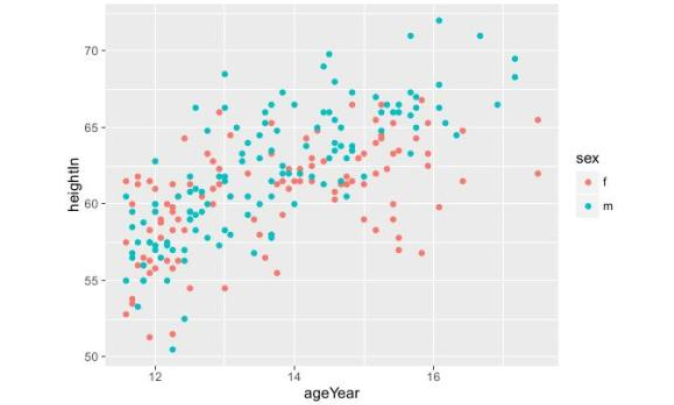
　　想要画出这些散点图的拟合曲线，也可以说是趋势曲线，我想，本文可教你，详情请耐心往下看。

方法一：np.polyfit

　　np.polyfit也是利用最小二乘多项式来拟合曲线的：

　　首先，先画出如上所示的散点图，大概看下散点分布趋势，究竟是像跟头发丝往上飘呢还是想落叶往下落呢？才能决定用哪种函数来拟合

　　假使选定多项式方程来拟合的话，那么首先得先求出多项式的各项系数，np.polyfit可以帮助我们求得多项式的系数，np.poly1d又可以帮助我们将系数代入原假设的方程中

k = np.polyfit(x, y, i)
func = np.poly1d(k)#将系数代入方程，得到方程式func

　　其中，i 为多项式的最高次数，假如i为3，那么多项式的基本方程为 y = k3*x^3 +k2*x^2+k1*x + b

　　得到的func方程，如果想要获得某个值所对应的的y值，可直接套用 y =  func（x）

方法二：leastsq

　　最小二乘法，即最小化的真实值和预测值的平方差之和。对于所有的散点，求出距离所有散点到曲线的距离平方和，使之最小化，即是拟合曲线

　　

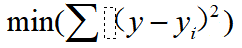
　　假使你不想用多项式来拟合曲线，想用其他函数，比如sin，cos，etc。那么，Scipy中optimize模块的leastsq可以帮助我们用最小二乘法拟合曲线趋势

　　定义一个函数方程，此处示例为三次方程，多项式的系数和常数项都放在Klist中

def func(klist,x):
    k1,k2,k3,b = klist
    #k1,k2,k3,b = klist[0],klist[1],klist[2],klist[3]
    return k1*x**3 + k2*x**2 + k3*x + b  

　　再定义一个偏差函数

##偏差函数：x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(klist,x,y):
    return func(klist,x)-y

　　由于leastsq已经将最小二乘法的”偏差平方”和”最小化”封装在函数中，所以偏差函数不用自行加“平方”

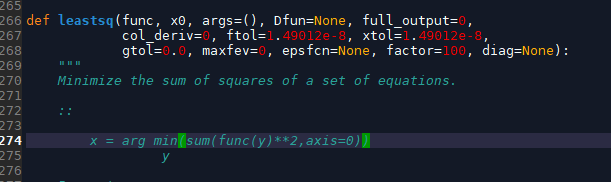
　　klist 为系数的初始值，args是除了系数之外的其他参数

klist = [0.01,0.01,0.01,0.0]
plesq = leastsq(error,x0 = klist,args=(x,y))

　　此时我们就可以得到用最小二乘法求得的拟合曲线系数啦

　　　　

 

　　在这里分享了两种最小二乘法拟合曲线的方法，以后还会继续完善python中最小二乘法的用法。看了请点个赞哦！