最小生成树 Prim算法 Kruskal算法实现

最小生成树定义

最小生成树是一副连通加权无向图中一棵权值最小的生成树。

在一给定的无向图 G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即

），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即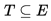

）且为无循环图，使得的 w(T) 最小，则此 T 为 G 的最小生成树。

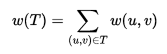
最小生成树其实是最小权重生成树的简称。

一个连通图可能有多个生成树。当图中的边具有权值时，总会有一个生成树的边的权值之和小于或者等于其它生成树的边的权值之和。广义上而言，对于非连通无向图来说，它的每一连通分量同样有最小生成树。

——以上内容摘自中文维基百科

通俗一点讲就是通过可行边遍历所有点，使这些边权值相加最小（可能吧）

Prim算法

类似于dijistra算法需要用到蓝白点的思想 ……不会dijistra也没关系不智障就够了

从单一顶点开始，普里姆算法按照以下步骤逐步扩大树中所含顶点的数目，直到遍及连通图的所有顶点。

输入：一个加权连通图，其中顶点集合为V，边集合为E；

初始化：V_new = {x}，其中x为集合V中的任一节点（起始点），E_new；

重复下列操作，直到V_new = V：

{

在集合E中选取权值最小的边（u, v），其中u为集合V_new中的元素，而v则是V中没有加入V_new的顶点（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

将v加入集合V_new中，将（u, v）加入集合E_new中；

}

输出：使用集合V_new和E_new来描述所得到的最小生成树。

图例	说明	不可选	可选	已选
	此为原始的加权连通图。每条边一侧的数字代表其权值。	-	-	-
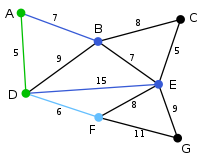
	顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。	C, G	A, B, E, F	D
	下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。	C, G	B, E, F	A, D
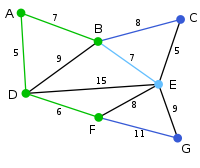
	算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。	C	B, E, G	A, D, F
	在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。	无	C, E, G	A, D, F, B
	这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。	无	C, G	A, D, F, B, E
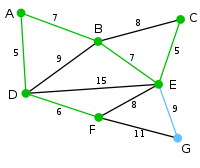
	顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。	无	G	A, D, F, B, E, C
	现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。	无	无	A, D, F, B, E, C, G