【算法】排序03——看着复杂其实就两步的堆排序(含代码实现)
1、堆排序效能简介
堆排序也是一种应用分治算法(建堆时应用了该思想)的排序方法,时间复杂度为无论在最好还是最坏情况下都为O[ n log(n)],相比于稳定的归并排序或是速度更胜一筹的快速排序(最好情况下O(n)),需要频繁进行交换以换取O(1)空间复杂度优势的堆排序,在如今大内存的硬件支持下似乎并没有如此的必要了。但是堆排序还是有它更特化的应用场景的,比如在大量数据中获取前Top几的记录。在这种情形下,堆排序实际比快排更高效。
2、什么是堆?它在序列中的表现形式如何?
想了解好堆排序,那首先得知道什么是堆,当然很多基础扎实的小伙伴肯定都知道,堆就是一个有着父节点大于(或小于)其子节点性质的完全二叉树(大于的是大顶堆,小于则是小顶堆)。
如果我们以一个序列(数组)来表现堆的话,按从堆顶先左右后上下的顺序标记下标的话,那就会有如下规律:
①下标为 i 的节点,其左孩子节点下标为 2i+1 ,右孩子下标为 2i+2 。
②非叶子节点的下标为 0 至 array.length/2 - 1 。
③如果一个节点只有一个叶子,那么它必然是左叶子。即一个节点的左叶子为空,那么这个节点必然是叶子节点。(实际上,只有最后一个非叶子节点才可能会有单叶子,即序列中下标为array.length/2 - 1的非叶子节点)
3、堆排序的流程
有一些小伙伴觉得堆排序有点复杂,看了动态演示图也觉得有点难,其实我个人观点觉得堆排序的更适合从逻辑角度理解,看堆排序的动态演示图反而更容易使人迷惑。
实际上,堆排序一共就做两大步:
第一步,建立堆,或者说将序列(数组)堆化。即2中我提到的,将堆在序列中表现出来。
在代码的实现中,我们建立堆的过程实际上就是应用了分治的思想,我们从最后一个非叶子节点开始堆化,然后逐渐向前对其他非叶子节点进行堆化,当我们堆化到子树更大的非叶子节点时,我们会发现,这些子树已经作为先前的小问题被我们堆化过,只要当前的非叶子节点在堆化时不用与孩子节点交换,我们就无需再对子树进行二次堆化。如下图:
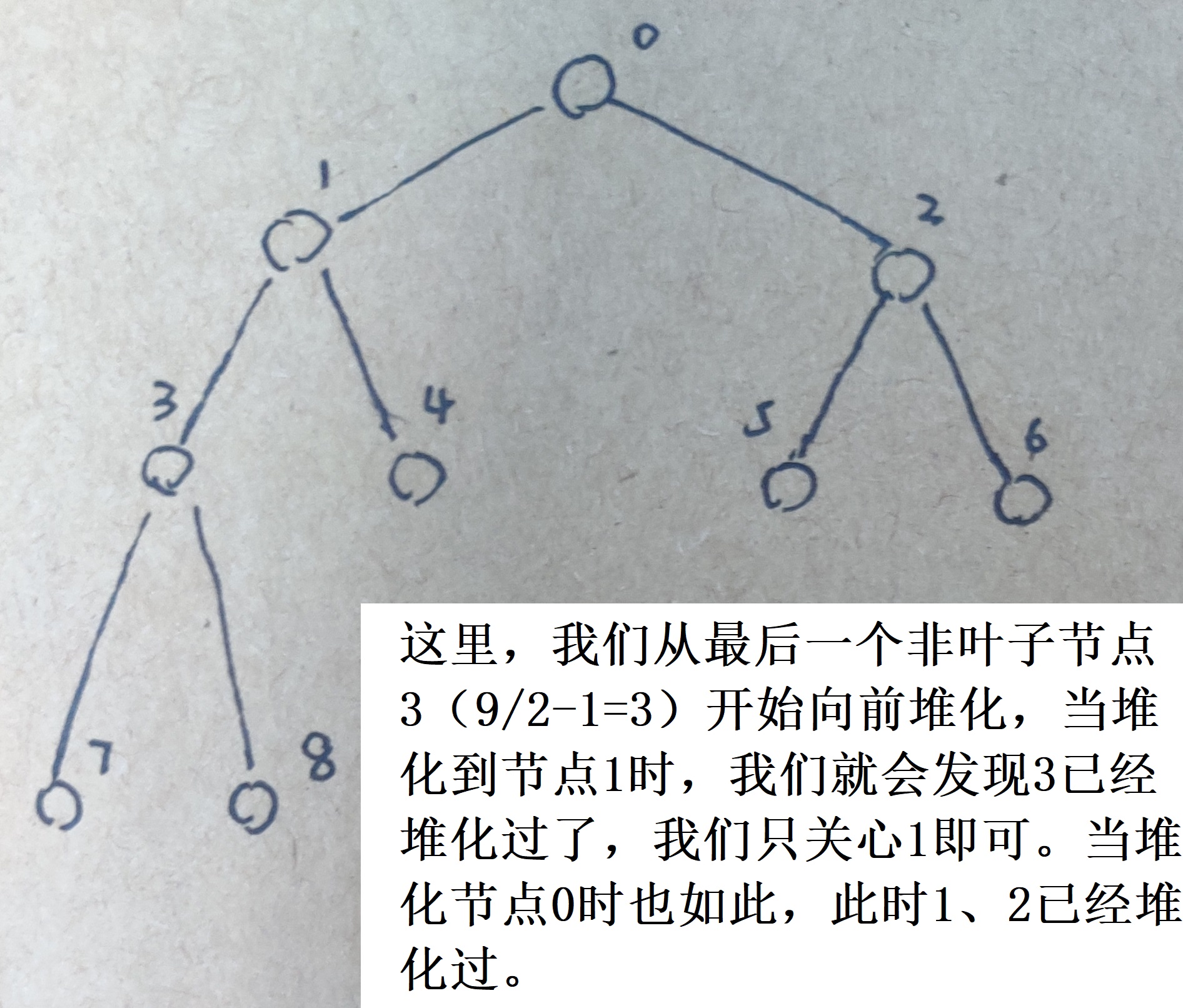
(再次注意,子树堆化过不代表它不会再变了,当需要堆化的节点要与其已经堆化的孩子节点交换时,我们还要在交换后对孩子节点再次堆化)
很多小伙伴看不懂堆排代码的第一个坎儿就在于没理解建堆时对分治思想的应用。
第二步,逐个把堆顶的元素(即最大值或最小值)拿出来扔到有序区,然后维护堆。
这里,我们逻辑上取出堆顶的元素放入有序区的流程在代码中其实只要用一个交换就可以实现,即堆顶元素与当前的堆尾元素交换。因为堆顶取走一个元素会使堆的大小减少一并破坏堆结构,但如果我们使堆顶与堆尾的元素交换,我们就会有两个好处:
一是可以把堆尾元素脱离堆(等效堆顶离堆)、并把它直接划入有序区;
二是由于堆尾离堆而不是堆顶离堆,所以没有破坏堆的结构,而且堆顶的子树仍是堆,我们只要对堆顶的元素进行堆化就可以,不用像第一步那样从后向前挨个儿堆化了。
怎么样?是不是很妙?
4、代码
1 import java.util.Arrays; 2 3 public class Main { 4 5 public static void heap_sort(int[] arr){ 6 //序列堆化,i指非叶子节点的下标 7 for (int i=arr.length/2-1 ; i>=0 ;i-- ){ 8 sort_node(arr,i,arr.length-1); 9 } 10 11 //交换堆顶堆尾,使堆尾脱离堆进入有序区。i指堆尾下标。 12 for(int i=arr.length-1 ; i>0 ; i--){ 13 // 堆顶的节点(最大值)与序列最后一个元素换位, 此时序列尾部逐渐有序化 14 int temp = arr[0]; 15 arr[0] = arr [i]; 16 arr[i] = temp; 17 //堆的规模开始减小,同时堆顶元素换了要进行维护 18 sort_node(arr,0,i-1); 19 } 20 } 21 22 /*对序列中某个节点进行堆化 23 * pointer指当前要堆化的节点 24 * end_edge指当前堆的最后一个节点 在 序列中的的下标 25 * */ 26 public static void sort_node (int[] arr, int pointer, int end_edge){ 27 int bigger_child ; 28 int left_child; 29 int right_child; 30 /* while的条件是判断跳出递归用的,不影响首次进入循环。若当前节点是叶子节点时, 31 就不再对该的节点堆化并跳出循环。由堆的性质可知,当左孩子为空时(即2*pointer+1越界), 32 当前节点必然是叶子节点*/ 33 while (2*pointer+1 <= end_edge){ 34 left_child = 2*pointer+1; 35 right_child = 2*pointer+2; 36 if(right_child > end_edge){//单叶子的情况(只可能右为空) 37 bigger_child = left_child; 38 }else {//双叶子的情况 39 bigger_child = arr[left_child]>arr[right_child]?left_child:right_child; 40 } 41 if(arr[pointer]<arr[bigger_child]){//判断较大子孩子与父亲的大小 42 //交换父子节点 43 int temp = arr[pointer]; 44 arr[pointer] = arr[bigger_child]; 45 arr[bigger_child] = temp; 46 pointer = bigger_child;//当前节点指针指向较大的孩子,递归,对该节点进行堆化 47 }else { 48 break; 49 } 50 } 51 } 52 53 public static void main(String[] args) { 54 //测试数据:5,6,9,8,7,4,1,2,3 55 int[] array = {5,6,4,45,1,2,33,6,7,99}; 56 heap_sort(array); 57 System.out.println(Arrays.toString(array)); 58 } 59 }
测试结果:

最后,如果小伙伴觉得这篇博文对你有帮助的话,就点个推荐吧



 浙公网安备 33010602011771号
浙公网安备 33010602011771号