DS博客作业07--查找

1.本周学习总结##

1.思维导图##

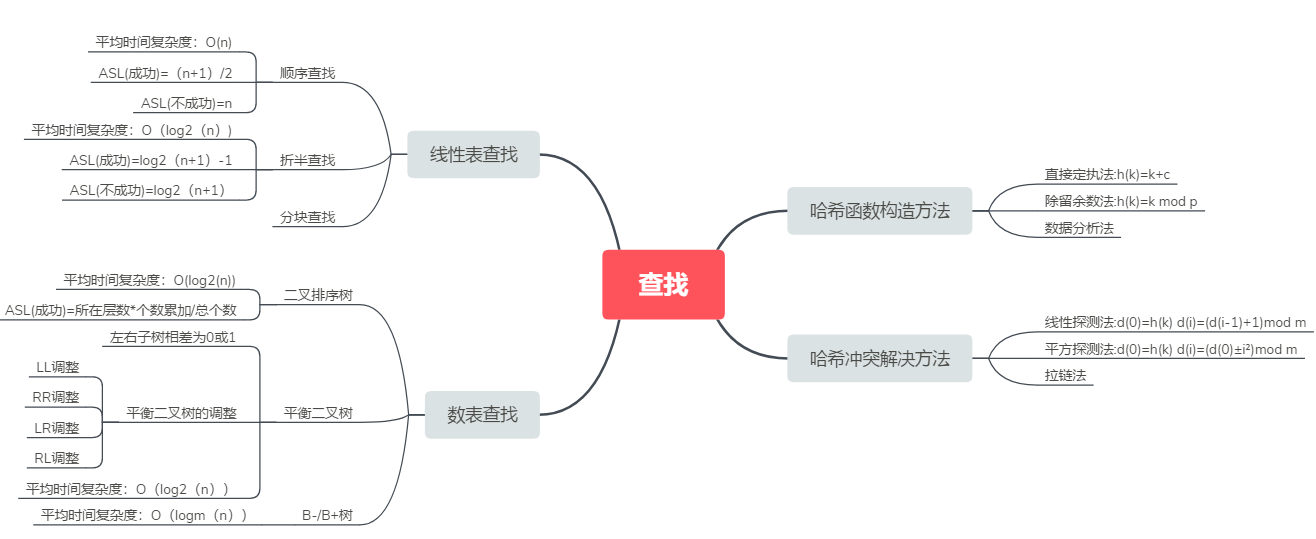
2.谈谈你对查找运算的认识及学习体会##

本章主要的知识就是第三部分树表的查找，包含：
①二叉排序树（特点：中序遍历后为有序序列）   在二叉排序树的删除步骤中，为保证树的有序性需要先判断删除结点的左右孩子情况，为空或一方为空，可以通过直接删除或非空子树替代删除：左右孩子不为空，则需要分布考虑
②平衡二叉树 特点平衡因子（结点的左右孩子高度差）≤1， 平衡二叉树的调整方法有：LL，RR,LR,RL调整
还有哈希表的查找：查找成功ASL=探测次数之和/哈希表中已有关键字之和    查找不成功ASL=关键字查找不成功次数之和/哈希表长度

2.PTA实验作业##

2.1.题目1：6-1 二叉搜索树的操作集##

2.1.1设计思路（伪代码）##

BinTree Delete(BinTree BST,ElementType X)
{
    定义tmp树结点
    if树空，直接输出"Not Found“
    else 找到要删除的X对应结点位置
    if X>当前结点 递归调用 Delete（BST->Right,X）
    if X<当前结点 递归调用 Delete（BST->Left,X）
    else if X=当前结点   判断当前结点左右孩子是否为空       
            if 左右孩子不空  
    调用函数FindMin(BST->Right)
    tmp->Data=BST->Data 保存数据
    BST树的右孩子置为结点 保证二叉搜索树的有序性
           else if
                   if左孩子为空， 右孩子置为结点
                   if右孩子为空，右孩子置为结点
    return BST
}

2.1.2代码截图##

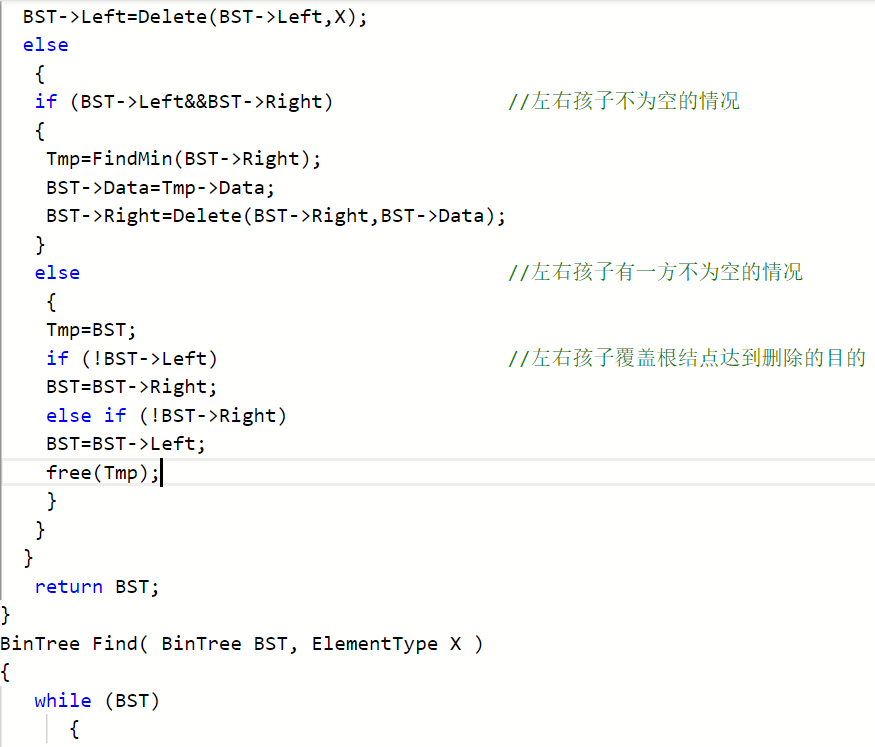
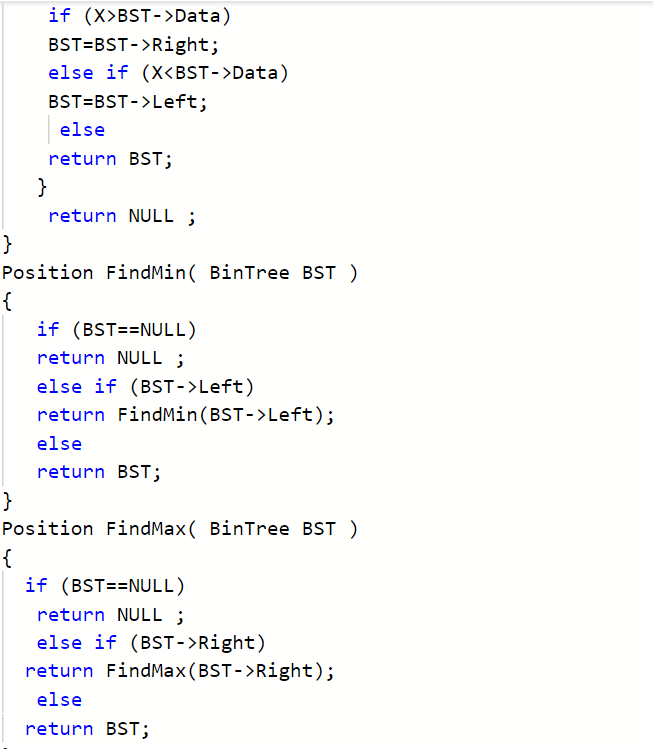
2.1.3本题PTA提交列表说明##

Q1：答案错误
A1：在判断树为空后，没有返回NULL，以及函数递归调用结点不正确，修改后改正
Q2：段错误：在删除结点函数中，考虑结点左右孩子不为空的情况，没有定义新的树结点来存储要删除结点
A2：定义新的树结点之后，在函数结束后释放释放结点的所占用的空间

2.2.题目：6-3 二叉搜索树中的最近公共祖先##

2.2.1设计思路（伪代码）##

int LCA(Tree T,int u,int v)
{
    if T 为空，返回 ERROR
    else if   (Find(T,u)且Find(T,v))   结点在树中
    if T->key>u且T->key<v且T->key>v且T->key<u   返回 结点T-key  
            end if
    if T->key=u或T->key=v  返回 结点T->key  
            end if
    if T->key>u或T->key>v 递归函数LCA（T->Left,u,v)   
            end if
    if T->key<u且T->key<v 递归函数LCA（T->Right,u,v)   
            end if
                 end if
    返回ERROR
}

2.2.2代码截图##

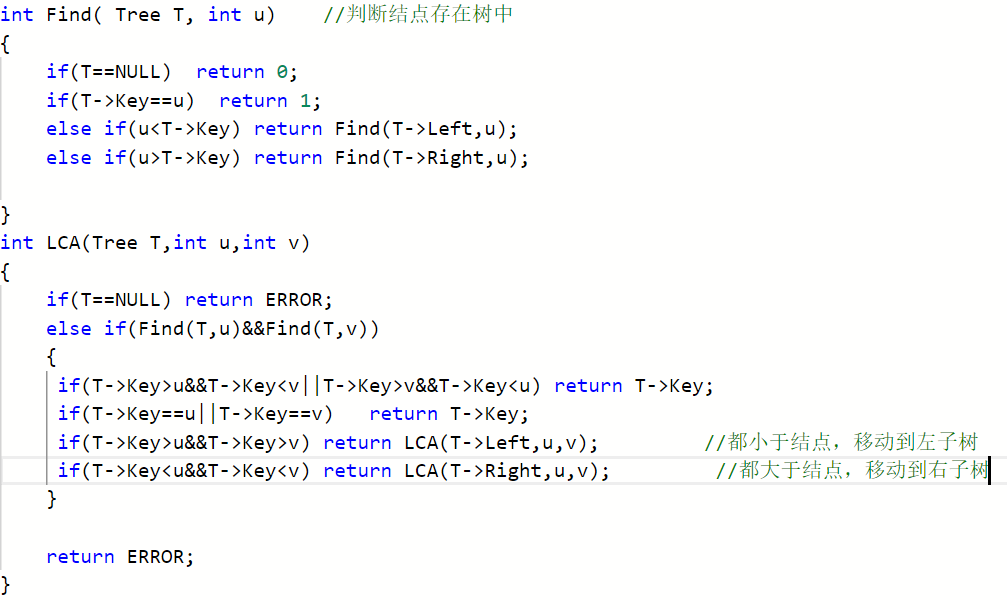
2.2.3本题PTA提交列表说明##

Q:部分正确 :测试点2：ERROR重定义  测试点6：两结点重合，但不在树中	  答案错误
A：树空以及结点为找到返回值从-1改为ERROR,结点重合的判断条件只需要判断一个即可，将”&&“改为”||“

2.3.题目：##

2.3.1设计思路（伪代码）##

2.3.2代码截图##

2.3.3本题PTA提交列表说明##

3、阅读代码##

3.1 题目##

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的##绝对值##不超过1。

3.2 解题思路##

先判断根结点，如果只有一个，则为1；
否则看左子树的深度减去右子树的深度等不等于1；
如果等于1，那么这颗二叉树就是平衡二叉树；
它的深度等于左右子数最大的深度+1；

3.3 代码截图##

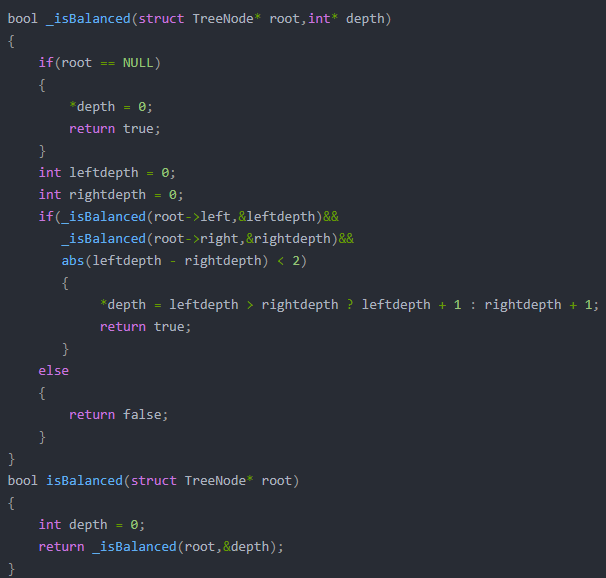
3.4 学习体会##

判断平衡二叉树，可以将二叉树拆分为左右子树两部分，通过递归调用函数分别判断左右子树是否也是平衡二叉树，进而判断整棵二叉树是否为平衡二叉树。题目要求平衡因子绝对值小于等于1，这里就需要运用到库函数 abs（）给平衡因子加绝对值