DS博客作业05-树

1.本周学习总结##

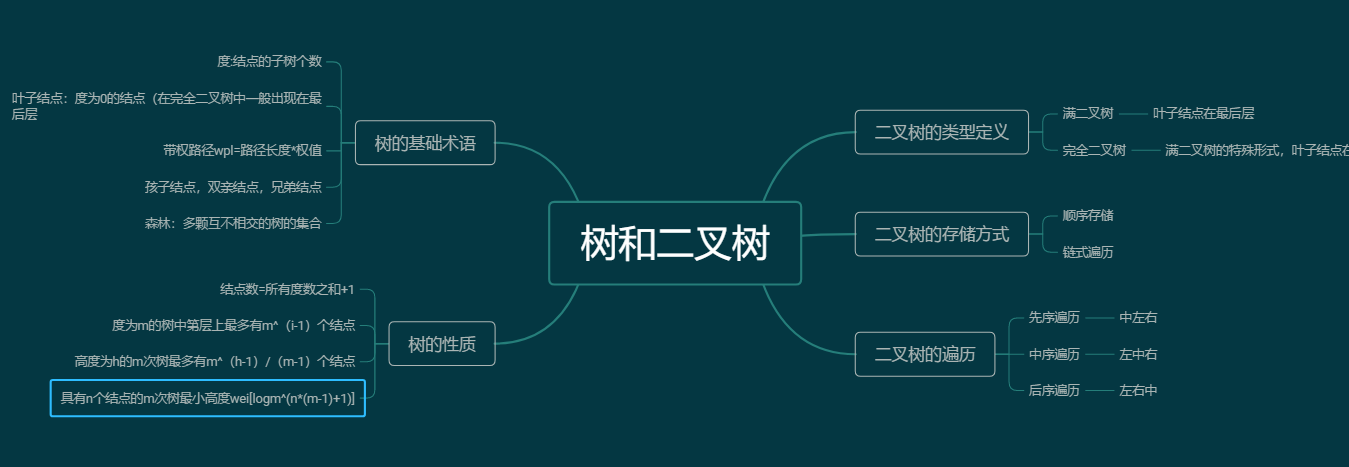
1.思维导图##

2.谈谈你对树结构的认识及学习体会##

1.树的学习主要注重于二叉树这一特征树，也包括树的基本知识，例如森林，度，叶子结点等等的基本术语。最重要的当然是二叉树，它由树根结点，左右子树组成。
2.二叉树有两种存储结构：链式存储、顺序存储。其中链式存储结构体中包括数据元素Data、左右孩子结点lchild和rchild，树的题集主要注重在建树函数上，通过对每个结点进行操作实现二叉树的建立，并且完成一些简单操作
3.二叉树的遍历主要有三种遍历方式
①先序遍历
访问根结点 先序遍历左子树 先序遍历右子树
②中序遍历
中序遍历左子树 访问根结点 中序遍历右子树
③后序遍历
后序遍历左子树 后序遍历右子树 访问根结点
上述三种遍历方式都要通过调用递归函数实现
4.二叉树中有种特殊的哈夫曼树：在n个带权叶子结点构成的所有二叉树中，带权路径长度WPL最小的二叉树成为哈夫曼树。哈夫曼树在构建结构体时多出了个权重值weight。通过权重weight便可得到WPL=各个叶子结点的值与所带权值相乘的累加值
例：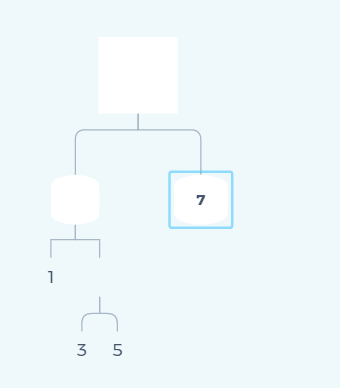
WPL=12+33+53+71=33

2.PTA实验作业##

2.1.题目1：7-1 还原二叉树##

2.1.1设计思路（伪代码）##

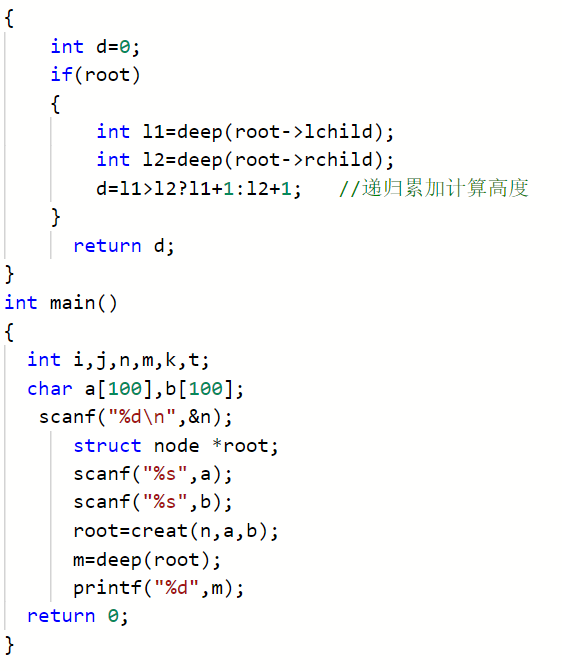
struct node *creat(int n,char a[],char b[]) //建树函数
{
    定义树根结点root
    定义字符指针p
    if n<0
    return NULL
    a[0]赋值root->Data;
    定义 t ，存放左孩子结点个数
    遍历中序序列  找出树根结点‘A'
    递归调用建树函数构建树的左右孩子
}

2.1.2代码截图##

2.1.3本题PTA提交列表说明。##

Q：求左孩子个数时，多将树根结点考虑到递归中，导致函数传参错误
A:通过定义H,找出问题并改正

2.2 题目:7-2 根据后序和中序遍历输出先序遍历##

2.2.1设计思路（伪代码）##

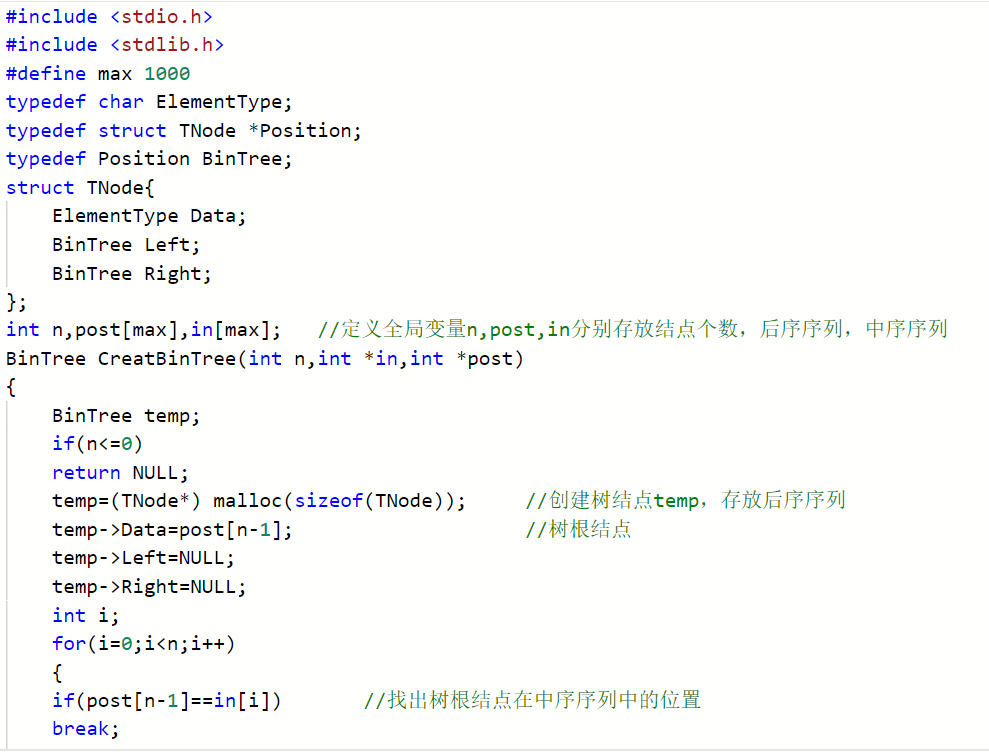
BinTree CreatBinTree(int n,int *in,int *post)
{
    定义树根结点temp
    if n<0
    return NULL
    申请结点temp；
    poost[n-1]赋值给temp->Data;
    树的左右孩子置为NULL
    遍历中序序列  找出树根结点‘A'
    递归调用递归函数构建树的左右孩子
}

2.2.2代码截图##

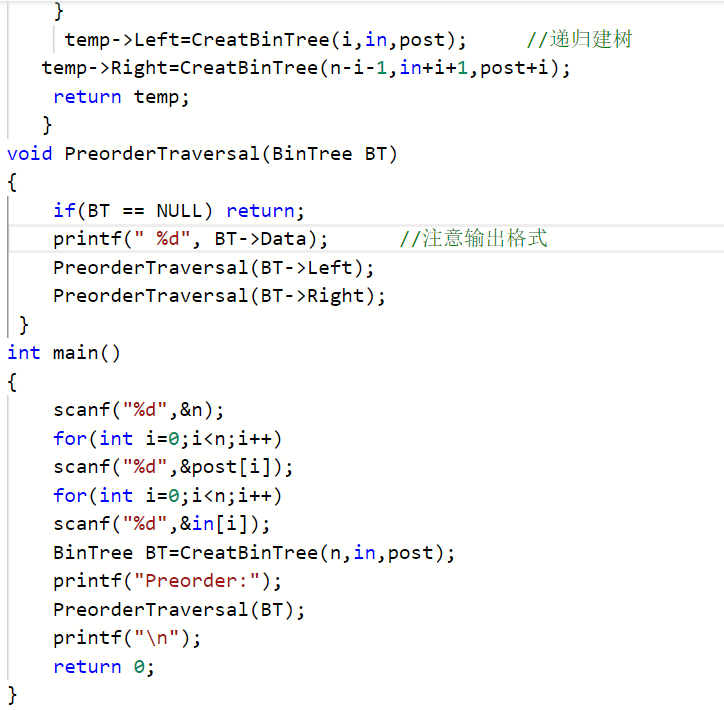
2.2.3本题PTA提交列表说明。##

Q:7-1与7-2相似，为什么要重复介绍
A1：其他的题目相对与自身较难，只会写这两题。
A2：虽然题型类似，但是解题细节也存在差异，相较于7-1，7-2时通过网上搜代码发现的方法，这串代码通过定义全局变量来进行函数的传参，虽然全局变量在构建工程时无法使用，但全局变量在某些题目中运用可以避免在不同函数中同一功能变量的重复定义以及考虑数据更改的问题

2.3 题目：7-4 jmu-ds-二叉树叶子结点带权路径长度和##

2.3.1设计思路（伪代码）##

int main()
{
    定义int 型变量h,wpl分别表示树层，带权路径长度，并置为0
    定义树根结点 T 
    GetWPL(T,0,wpl);   求带权路径长度wpl
}

BTree CreateBtree(string str,int i)
{
    定义树根结点 BT，length
    把str.size()赋值给length
    if i>length-1或i<=0
    return NULL
    if str[i]='#'
    return NULL
    把str字符串数组中非'#'的字符赋值给BT->Data
    递归调用建树函数CreateBtree：左孩子  下标为2*i，右孩子 下标为2*i+1
    return BT
}

void GetWPL( BTree BT ,int h,int &wpl) 
{
    if BT为空
    return NULL
    else  if左右孩子不为空
    wpl=wpl+(BT->Data-'0')*h   字符转数字
    递归调用GetWPL   求wpl
}

2.3.2代码截图##

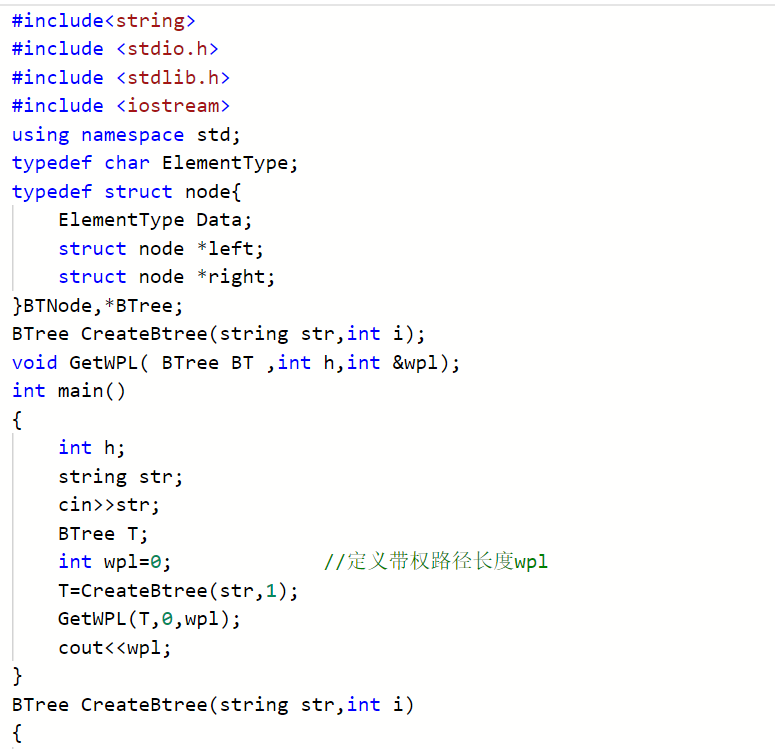
2.3.3本题PTA提交列表说明##

Q1:编译错误
A1：主要出在某些变量的定义上，以及h高度的初始值为0或1的问题上
Q2：部分正确，只通过树空的测试点，其他测试点显示答案错误
A2：放在编译器上运行，程序突然终止便退出，修改wpl的形式，问题并没有解决；通过观察主函数，了解问题在于漏写'' cin>>str;'‘并且在建树函数部分中递归调用建树函数修改右孩子下标为i*2+1.
cin>>str;'

3、阅读代码##

3.1 题目:将一棵树对称（镜像）后输出##

3.2 解题思路##

先序遍历这棵树的每个结点，如果遍历到的结点有子结点，则交换它的两个子结点。当交换完所有非叶子结点的左右子结点之后，就得到了树的镜像。

3.3 代码截图##

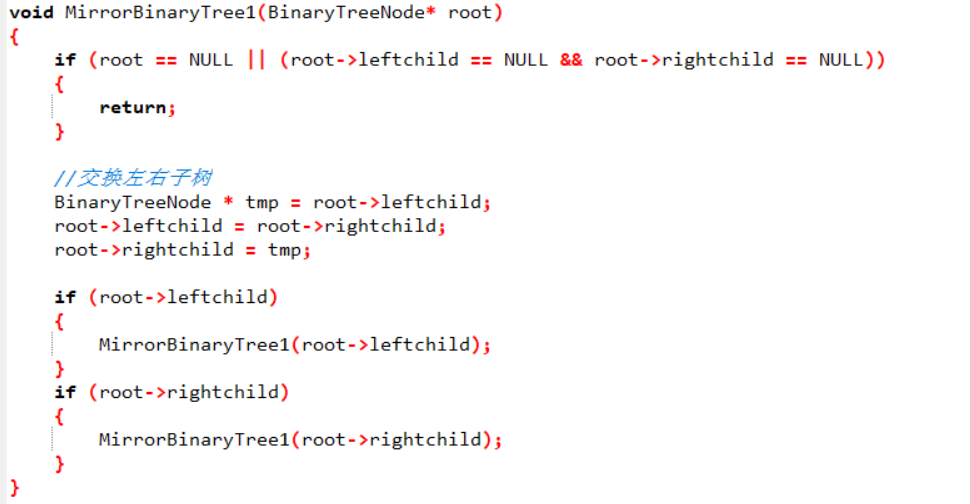
3.4 学习体会##

在对树中的元素，无论是左右孩子结点还是数据元素Data，都要注意考虑它们的值是否为空。将一个树对称镜像输出建议运用先序遍历，因为是对称输出，而先序遍历是先访问根结点，再遍历左右孩子结点，这样只需要考虑左右结点的值互换即可。