Kaggle Master解释梯度提升(Gradient Boosting)(译)
如果说线性回归算法像丰田凯美瑞的话,那么梯度提升(GB)方法就像是UH-60黑鹰直升机。XGBoost算法作为GB的一个实现是Kaggle机器学习比赛的常胜将军。不幸的是,很多从业者都只把这个算法当作黑盒使用(包括曾经的我)。这篇文章的目的就是直观而全面的介绍经典梯度提升方法的原理。

原理说明
我们先从一个简单的例子开始。我们想要基于是否打电子游戏、是否享受园艺以及是否喜欢戴帽子三个特征来预测一个人的年龄。我们的目标函数是最小化平方和,将用于训练我们模型的训练集如下:
| ID | 年龄 | 喜欢园艺 | 玩电子游戏 | 喜欢戴帽子 |
| 1 | 13 | False | True | True |
| 2 | 14 | False | True | False |
| 3 | 15 | False | True | False |
| 4 | 25 | True | True | True |
| 5 | 35 | False | True | True |
| 6 | 49 | True | False | False |
| 7 | 68 | True | True | True |
| 8 | 71 | True | False | False |
| 9 | 73 | True | False | True |
我们对数据可能有以下直觉:
- 喜欢园艺的人可能年纪偏大
- 喜欢电子游戏的人可能更年轻
- 喜欢戴帽子可能跟年纪关系不大
对于这些直觉我们可以很快在数据中检验
| 特征 | False | True |
| 喜欢园艺 | 「13,14,15,35」 | 「25,49,68,71,73」 |
| 玩电子游戏 | 「49,71,73」 | 「13,14,15,25,35,68」 |
| 喜欢戴帽子 | 「14,15,49,71」 | 「13,25,35,68,73」 |
现在我们尝试用回归树来建模数据。开始时,我们要求每个叶子结点都至少有三个数据点。这样回归树会从喜欢园艺这个特征开始分裂(split),发现满足条件,分裂结束。结果如下图:
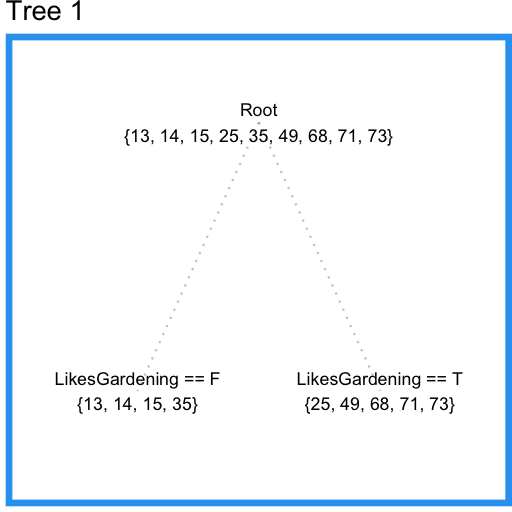
结果还不错,不过我们没有用上玩电子游戏这个特征。现在我们尝试将限制条件改为叶子结点要有两个数据点。结果如下:
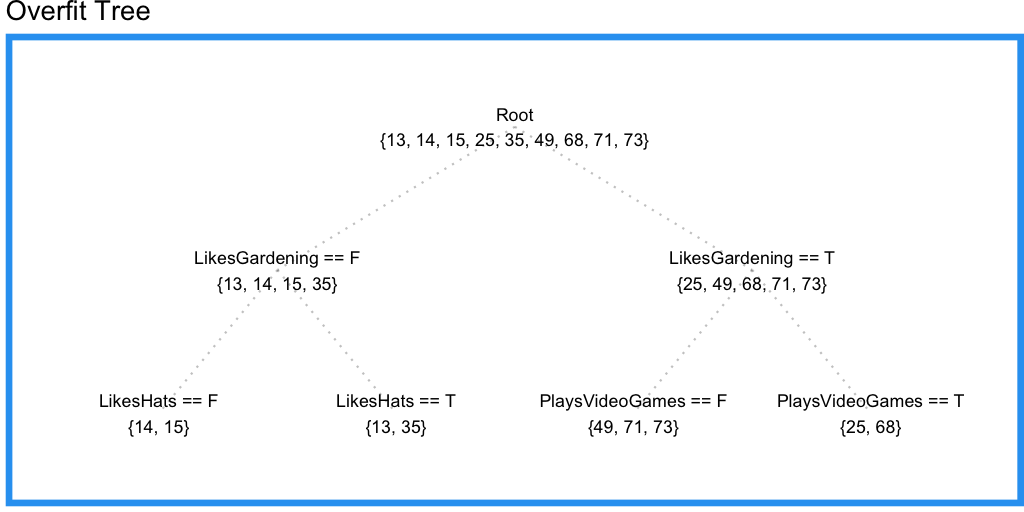
这棵树中我们三个特征都用上了,但喜欢戴帽子这个特征多少与年龄无关,这意味着我们的回归树可能过拟合了。
此例中我们可以看出使用单个决策/回归树(decision/regression tree)的缺点:它无法叠加两个有重叠区域的有效特征(例如:喜欢园艺和玩电子游戏)。假设我们测量第一颗树的训练误差,结果将如下所示:
| ID | 年龄 | Tree1 预测结果 | Tree1 预测残差(Residual) |
| 1 | 13 | 19.25 | -6.25 |
| 2 | 14 | 19.25 | -5.25 |
| 3 | 15 | 19.25 | -4.25 |
| 4 | 25 | 57.2 | -32.2 |
| 5 | 35 | 19.25 | 15.75 |
| 6 | 49 | 57.2 | -8.2 |
| 7 | 68 | 57.2 | 10.8 |
| 8 | 71 | 57.2 | 13.8 |
| 9 | 73 | 57.2 | 15.8 |
现在我们可以用另一棵树Tree2来拟合Tree1的预测残差,结果如下:
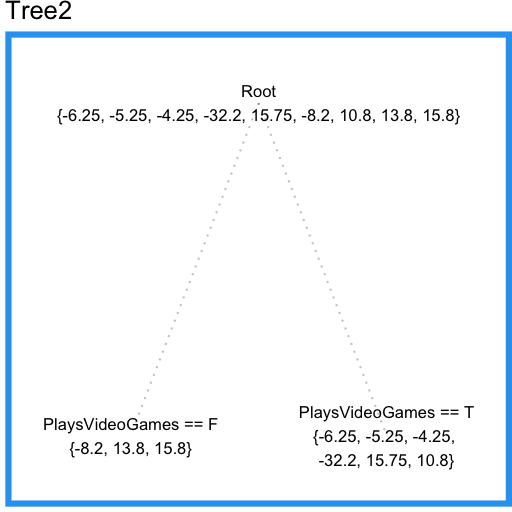
现在我们可以注意到这颗回归树没有包括喜欢帽子这个特征(之前过拟合的回归树使用了这个特征)。这是因为这棵回归树可以在全体样本上考察特征,而之前过拟合的单棵回归树只能在局部考察特征。
现在我们可以在第一棵回归树的基础上加上第二棵“纠错”的回归树,结果如下:
| PersonID |
Age | Tree1 Prediction | Tree1 Residual | Tree2 Prediction | Combined Prediction | Final Residual |
|---|---|---|---|---|---|---|
| 1 | 13 | 19.25 | -6.25 | -3.567 | 15.68 | 2.683 |
| 2 | 14 | 19.25 | -5.25 | -3.567 | 15.68 | 1.683 |
| 3 | 15 | 19.25 | -4.25 | -3.567 | 15.68 | 0.6833 |
| 4 | 25 | 57.2 | -32.2 | -3.567 | 53.63 | 28.63 |
| 5 | 35 | 19.25 | 15.75 | -3.567 | 15.68 | -19.32 |
| 6 | 49 | 57.2 | -8.2 | 7.133 | 64.33 | 15.33 |
| 7 | 68 | 57.2 | 10.8 | -3.567 | 53.63 | -14.37 |
| 8 | 71 | 57.2 | 13.8 | 7.133 | 64.33 | -6.667 |
| 9 | 73 | 57.2 | 15.8 | 7.133 | 64.33 | -8.667 |
| Tree1 SSE | Combined SSE |
|---|---|
| 1994 | 1765 |
梯度提升方案1
受上面“纠错”树的启发,我们可以定义以下梯度提升方法:
- 用一个模型来拟合数据 F1(x)= y
- 用另一个模型来拟合前一个模型预测的残差 h1(x)= y - F1(x)
- 用残差模型和原模型之和创建一个新模型 F2(x)= F1(x) + h1(x)
我们可以很容易想到插入更多的模型来纠正之前模型的错误(译注,resnet可以看作一个例子):
FM(x) = FM-1(x) + hM-1(x), F1(x) 为初始模型
因为我们第一步初始化了模型F1(x),我们接下来每一步的任务是拟合残差: hm(x) = y - Fm(x).
现在我们停下来观察一下,我们只是说hm是一个“模型”-并没有说它一定要是一个基于树的模型。这就是梯度提升的一个优点,我们可以轻松引入任何模型,也就是说梯度提升只是用来迭代提升弱模型的。虽然理论上我们的弱模型可以是任何模型,但是实践中它几乎总是基于树的,所以我们现在把hm就当作回归树也没有什么问题。
梯度提升方案2
我们现在来尝试像大多数梯度提升实现一样初始化-将模型初始化为只输出单一预测。因为我们的任务目前是最小化平方和误差,我们可以让初始化F0为预测训练样本的均值:
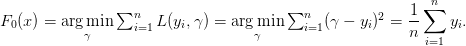
现在我们可以递归的定义我们后续的模型了:
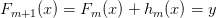 ,for
,for 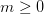
其中hm是基础模型之一,例如回归树。
这时你可能会考虑一个问题:如何选取超参数m。 换句话说,我们该用多少次这种残差校正过程。一种方法是,最佳的m可以通过使用交叉验证(cross-validation)来测试不同的m来确定。
梯度提升方案3
到现在为止我们的目标都是最小化方差和(L2),但如果我们想最小化绝对值误差和呢(L1)?我们很容易想到通过改变我们基础模型(回归树)的目标函数来实现这个,但这么做有几个缺点:
- 数据量较大时计算上可能很昂贵(每次分裂我们都需要遍历以找到中位数)
- 上面所说的GB不限制基础模型的特性将消失,这样我们将只能用支持此目标函数的基础模
让我们试着找找一个更漂亮的解决方案。回顾一下上面的例子,我们会让F0预测训练样本的中位数,也就是35,来最小化绝对值和。现在我们能计算F0的预测残差了:
| PersonID | Age | F0 | Residual0 |
|---|---|---|---|
| 1 | 13 | 35 | -22 |
| 2 | 14 | 35 | -21 |
| 3 | 15 | 35 | -20 |
| 4 | 25 | 35 | -10 |
| 5 | 35 | 35 | 0 |
| 6 | 49 | 35 | 14 |
| 7 | 68 | 35 | 33 |
| 8 | 71 | 35 | 36 |
| 9 | 73 | 35 | 38 |
观察到第一个和第四个训练样本的预测残差为-22和-10. 假设我们能让每个预测都离各自的真实值更近1个单位,这样样本1和样本4的平方和误差将分别减少43和19,而两者绝对值误差都将减少1。通过上面的计算我们可以发现,使用平方误差的回归树会主要关注减少第一个训练样本的预测残差,而使用绝对值误差的回归树会同样关注这两个样本。现在我们接着训练h0来拟合F0的预测残差,与之前不同的是,我们将使用F0的预测损失函数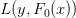 的导数来训练h0。使用绝对值误差时,hm只是考虑Fm预测残差的符号(平方误差时还会考虑残差的大小)。在h中的样本被分到各个叶子结点之后,每个叶子结点的平均梯度就能被计算出来并加权
的导数来训练h0。使用绝对值误差时,hm只是考虑Fm预测残差的符号(平方误差时还会考虑残差的大小)。在h中的样本被分到各个叶子结点之后,每个叶子结点的平均梯度就能被计算出来并加权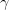 用于更新模型:
用于更新模型: 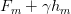 (这样各叶子结点的损失将减少,实际使用中个叶子结点的权重
(这样各叶子结点的损失将减少,实际使用中个叶子结点的权重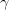 可能不同)。
可能不同)。
梯度下降 (Gradient Descent)
现在让我们用GD让上述想法更形式化一点。考虑如下可导损失函数:
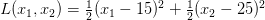
目标是找到一对 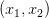 来最小化 L。我们可以注意到这个损失函数可以看作计算两个数据点的均方差,两个数据点的真实值分别为 15 和 25。虽然我们能解析的找到这个损失函数的最小值,但GD能帮我们优化更复杂的损失函数(也许不能找到解析解)。
来最小化 L。我们可以注意到这个损失函数可以看作计算两个数据点的均方差,两个数据点的真实值分别为 15 和 25。虽然我们能解析的找到这个损失函数的最小值,但GD能帮我们优化更复杂的损失函数(也许不能找到解析解)。
初始化:
总迭代数 M = 100
起始预测 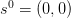
步长 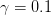
For iteration to
:
1. 计算 在上次预测点
处的梯度
2. 将预测点向最陡梯度方向移动步长 ,也就是
如果步长 够小且M足够大的话, 最终预测sM将会收敛到L的最小值。
利用梯度下降
现在让我们在梯度提升模型中使用GD。将我们的目标函数记为L,起始模型记为F0(x)。在迭代次数 m = 1时,计算L对F0(x)的梯度。然后我们用一个弱模型拟合梯度,以使用回归树为例,叶子结点中有相似特征的样本中会计算出平均梯度,然后使用平均梯度来更新模型,得到F1。重复此过程直到我们得到Fm。
整理一下利用GD的梯度提升算法,描述如下:
初始化:
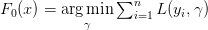
For m = 1 to M:
计算伪残差:
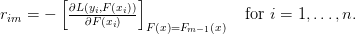
用 拟合伪残差
拟合伪残差
计算步长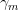 (决策树的情况可以给每个叶子结点单独分配步长)
(决策树的情况可以给每个叶子结点单独分配步长)
更新模型 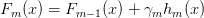
为帮助你验证是否理解梯度提升算法,以下分别给出对例子问题使用L1和L2目标函数的结果。
L2损失函数
| Age | F0 |
Pseudo Residual0 | h0 | gamma0 | F1 |
Pseudo Residual1 | h1 | gamma1 | F2 |
|---|---|---|---|---|---|---|---|---|---|
| 13 | 40.33 | -27.33 | -21.08 | 1 | 19.25 | -6.25 | -3.567 | 1 | 15.68 |
| 14 | 40.33 | -26.33 | -21.08 | 1 | 19.25 | -5.25 | -3.567 | 1 | 15.68 |
| 15 | 40.33 | -25.33 | -21.08 | 1 | 19.25 | -4.25 | -3.567 | 1 | 15.68 |
| 25 | 40.33 | -15.33 | 16.87 | 1 | 57.2 | -32.2 | -3.567 | 1 | 53.63 |
| 35 | 40.33 | -5.333 | -21.08 | 1 | 19.25 | 15.75 | -3.567 | 1 | 15.68 |
| 49 | 40.33 | 8.667 | 16.87 | 1 | 57.2 | -8.2 | 7.133 | 1 | 64.33 |
| 68 | 40.33 | 27.67 | 16.87 | 1 | 57.2 | 10.8 | -3.567 | 1 | 53.63 |
| 71 | 40.33 | 30.67 | 16.87 | 1 | 57.2 | 13.8 | 7.133 | 1 | 64.33 |
| 73 | 40.33 | 32.67 | 16.87 | 1 | 57.2 | 15.8 | 7.133 | 1 | 64.33 |

L1 损失函数
| Age | F0 |
Pseudo
Residual0 | h0 | gamma0 | F1 |
Pseudo Residual1 | h1 | gamma1 | F2 |
|---|---|---|---|---|---|---|---|---|---|
| 13 | 35 | -1 | -1 | 20.5 | 14.5 | -1 | -0.3333 | 0.75 | 14.25 |
| 14 | 35 | -1 | -1 | 20.5 | 14.5 | -1 | -0.3333 | 0.75 | 14.25 |
| 15 | 35 | -1 | -1 | 20.5 | 14.5 | 1 | -0.3333 | 0.75 | 14.25 |
| 25 | 35 | -1 | 0.6 | 55 | 68 | -1 | -0.3333 | 0.75 | 67.75 |
| 35 | 35 | -1 | -1 | 20.5 | 14.5 | 1 | -0.3333 | 0.75 | 14.25 |
| 49 | 35 | 1 | 0.6 | 55 | 68 | -1 | 0.3333 | 9 | 71 |
| 68 | 35 | 1 | 0.6 | 55 | 68 | -1 | -0.3333 | 0.75 | 67.75 |
| 71 | 35 | 1 | 0.6 | 55 | 68 | 1 | 0.3333 | 9 | 71 |
| 73 | 35 | 1 | 0.6 | 55 | 68 | 1 | 0.3333 | 9 | 71 |

梯度提升方案4
逐渐缩小步长/学习率(shrinkage),以帮助稳定收敛。
梯度提升方案5
行采样和列采样。不同采样技术之所以有效是因为不同采样回导致不同的树分叉-这意味着更多的信息。
实战中的梯度提升
梯度提升算法在实战中十分有效。其中最流行的实现 XGBoost 在 Kaggle 的比赛中屡次获奖。XGBoost 使用了许多小技巧来加速和提高准确率(特别是二阶梯度下降)。来自微软的LigtGBM最近也吸引了不少目光。
梯度提升算法还能做些什么呢?除了回归(regression),分类和排名也可以用到-只要损失函数是可微即可。分类应用中二元分类常用logistic function作损失函数,多元分类用softmax作损失函数。
原文链接:http://blog.kaggle.com/2017/01/23/a-kaggle-master-explains-gradient-boosting/


