20210714 noip15
考前
mtr 中午拿着笔记本改题(Orz),一点多发现 13.50 有比赛(截止 12 点都没放出来),赶紧睡。13.40 到了学校,巨瞌睡,洗了把脸到机房发现推迟到 14.30 了,wcnm
趴在桌上睡觉,Orz 抓紧时间打 luogu 月赛的大佬
考场
T1 集体讨论得 dead line 是直线,感觉有点像《仪仗队》,打出 \(n,m\le3\) 的表发现似乎可以枚举以形成直线的两点为对角的矩形算,跳了
T2 想到了正确性不明 \(O(n\log^2 n)\) 点分治,但本人分治学的很烂就没准备写(ys 巨佬考场就写了出来,切了),想到了从大到小加点,并查集维护直径,但不知道如果直径不过当前点怎么办,跳了跳了
T3 一眼线段树求没有花精的区间中最长的,稍微划拉了一下如何 up,感觉可做,毕竟数据结构算是我的强项
怕 T3 写不完,15.20 就开始写了。
回来看 T1,先写完了假做法,发现在 \(3\times4\) 的时候就挂了,看上去要容斥。又开始尝试每次以最下、最右的点为一个端点,用欧拉函数算贡献,然后把这些点去掉,但想不清楚,最后写了暴力跑路
T2 裸暴力
大概 16.00 开始写 T3,先手推清楚了具体如何 up,问题是在线段树的每个节点上开了个结构体(重载小于号),常数巨大。17.00 写完,调了调边界就过了小样例,发现就这个题没大样例。。。只能对拍。结果没拍几组就挂了。慌得一比,调小数据发现比较区间哪个优是不能直接比区间中点到两边的距离,因为 \(0,n+1\) 两个位置上没有花精,改了改重载小于号终于在 17.20 过拍了。。。
交题时怕 T1 MLE,\(N\) 从 \(2\times10^7\) 改到了 \(40^4\)。最后又觉得能多骗分,想着平时能开 \(5\times10^7\) 个 int,于是开到了 \(10^7\)
res
rk1 0+55+100
T1 MLE。平时能恰好开 \(6\times10^7\) 个 int 是因为有 256M,但这题只有 128M。。。
T2 卡常过了一些点
rk2 赵旭兵 60+30+60
rk6 ys 0+100+0
夜莺与玫瑰
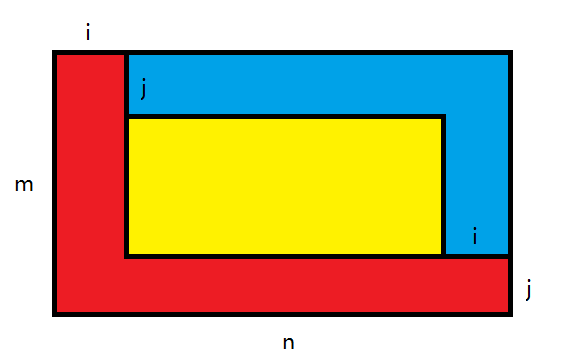
枚举方向向量 \((i,j)\),显然有 \(\gcd(i,j)=1\),设这条直线与给定矩形的点的交点为 \((x,y)\),那就统计满足 \((x-i,y-j)\) 在矩形内,\((x+i,y+j)\) 不在矩形内的 \((x,y)\)(即 \((x,y)\) 是这条直线与矩形的最后一个交点,下图中蓝色)。不难算出答案为:
理解:
首先 \(i,j\) 要互质,其次 \((x-i,y-j)\) 在矩形内的 \((x,y)\) 有 \((n-i)(m-j)\) 个(黄色+蓝色),\((x+i,y+j)\) 也在矩形内的有 \((n-2i)(m-2j)\) 个(黄色),容斥一下即可。
由于 \(n\le4000\),可以二维前缀和预处理答案。一个问题是需要卡空间,一个大问题是数据中有 \(n,m=4001\) 的点,出题人我问候你。
基于这个相同的式子,有时间 \(O(n^2+Tn)\),空间 \(O(n^2)\) 的做法。
基于莫比乌斯反演,有时间 \(O(n+Tn)\),空间 \(O(n)\) 的做法。
code
#define int unsigned
const int N = 4004, mod = (1<<30)-1;
int T,n,m;
int ans[N+8][N+8],a[N+8][N+8];
bitset<N+8> is[N+8];
signed main() {
// freopen("a.in","r",stdin);
// freopen("a.out","w",stdout);
is[1][0] = 1;
For(i,1,N) For(j,1,N) is[i][j] = is[min(i,j)][max(i,j)%min(i,j)];
////////// nm项 ij项
For(i,1,N-1) For(j,1,N-1) if( is[i][j] ) {
++ans[i+1][j+1], a[i+1][j+1] += i*j;
if( i < 2e3+2 && j < 2e3+2 )
--ans[i<<1|1][j<<1|1], a[i<<1|1][j<<1|1] -= 4*i*j;
}
For(i,1,N) For(j,1,N)
ans[i][j] += ans[i-1][j] + ans[i][j-1] - ans[i-1][j-1],
a[i][j] += a[i-1][j] + a[i][j-1] - a [i-1][j-1];
// ans[n][m]: gcd(1..n,1..m)=1的个数(nm项的系数)
// a[n][m]: ij项
For(i,1,N) For(j,1,N) ans[i][j] = ans[i][j]*i*j + a[i][j];
////////// im项 jn项
memset(a,0,sizeof a);
For(i,1,N-1) For(j,1,N-1) if( is[i][j] ) {
a[i+1][j+1] -= i;
if( i < 2e3+2 && j < 2e3+2 ) a[i<<1|1][j<<1|1] += i<<1;
}
For(i,1,N) For(j,1,N)
a[i][j] += a[i-1][j] + a[i][j-1] - a[i-1][j-1],
// a[n][m]: i in [1,n],j in [1,m],gcd(i,j)=1的i的和
ans[i][j] += j*a[i][j]; // 此处的j为式子中的m
memset(a,0,sizeof a);
For(i,1,N-1) For(j,1,N-1) if( is[i][j] ) {
a[i+1][j+1] -= j;
if( i < 2e3+2 && j < 2e3+2 ) a[i<<1|1][j<<1|1] += j<<1;
}
For(i,1,N) For(j,1,N)
a[i][j] += a[i-1][j] + a[i][j-1] - a[i-1][j-1],
ans[i][j] += i*a[i][j];
read(T);
while( T-- ) {
read(n,m);
// assert(n<=4000),assert(m<=4000);
write((n+m+2*ans[n][m])&mod);
}
return ioclear();
}
影子
考场上其实想的差不多
每次合并完并查集后,用当前点点权乘上直径更新答案即可。因为是用当前点来合并连通块,因此如果直径的两个端点在原来的联通块中,那么这次的答案一定不比那时算出来的优(点权不会变大);否则直径一定会过当前点
code
const int N = 1e5+5;
int T,n,mm,val[N],head[N];
struct Edge { int to,w,nxt; } e[N*2];
int id[N];
struct DSU {
int fa,p,q;
LL d;
} s[N];
namespace dist {
int fa[N],dep[N],siz[N],son[N],top[N];
LL d[N];
void dfs1(int u,int f) {
dep[u] = dep[ fa[u]=f ]+1, siz[u] = 1, son[u] = 0;
for(int i = head[u], v; i; i = e[i].nxt) if( (v=e[i].to) != f ) {
d[v] = d[u] + e[i].w;
dfs1(v,u);
siz[u] += siz[v];
if( siz[v] > siz[son[u]] ) son[u] = v;
}
}
void dfs2(int u,int t) {
top[u] = t;
if( son[u] ) dfs2(son[u],t);
for(int i = head[u], v; i; i = e[i].nxt)
if( (v=e[i].to) != fa[u] && v != son[u] ) dfs2(v,v);
}
void init() { dfs1(1,0), dfs2(1,1); }
int lca(int u,int v) {
while( top[u] != top[v] ) {
if( dep[top[u]] < dep[top[v]] ) swap(u,v);
u = fa[top[u]];
}
return dep[u]<dep[v] ? u : v;
}
LL dis(int u,int v) { return d[u]+d[v]-d[lca(u,v)]*2; }
}
using dist::dis;
int find(int x) { return s[x].fa==x ? x : s[x].fa=find(s[x].fa); }
void up(int x,int p,int q) {
LL d = dis(p,q);
if( d > s[x].d ) s[x].p = p, s[x].q = q, s[x].d = d;
}
void merge(int x,int y) {
if( x == y ) return;
s[y].fa = x;
int p = s[x].p, q = s[x].q;
up(x,s[y].p,s[y].q);
up(x,p,s[y].p), up(x,p,s[y].q), up(x,q,s[y].p), up(x,q,s[y].q);
}
void solve() {
LL ans = 0;
read(n);
For(i,1,n) read(val[i]), id[i] = i, s[i] = (DSU){i,i,i,0};
for(int i = 1; i < n; ++i) {
int x,y,z; read(x,y,z);
e[++mm] = (Edge){y,z,head[x]}, head[x] = mm;
e[++mm] = (Edge){x,z,head[y]}, head[y] = mm;
}
dist::init();
sort(id+1,id+n+1,[](const int &x,const int &y){return val[x]>val[y];});
For(i,1,n) {
int u = id[i];
for(int j = head[u], v; j; j = e[j].nxt)
if( val[ v=e[j].to ] >= val[u] ) merge(find(u),find(v));
ans = max(ans,val[u]*s[find(u)].d);
}
write(ans,10);
}
signed main() {
read(T);
while( T-- ) {
mm = 1;
mem(head,0,n);
solve();
}
return ioclear();
}
玫瑰花精
线段树
考场 code
const int N = 2e5+5, M = 1e6+5;
int n,m;
int pos[M];
struct Seg {
int l,r;
int len() {
if( l == 1 ) return r;
if( r == n ) return n-l+1;
return (l+r>>1)-l+1;
}
Seg(int l=0,int r=0):l(l),r(r){}
};
bool operator < (Seg x,Seg y)
{ return x.len()!=y.len() ? x.len()>y.len() : x.l<y.l; }
struct Node {
int l,r,lr,rl;
// lr: 从左往右最后一个没占的地方
Seg a;
} t[N*4];
void up(int u) {
int ls = u<<1, rs = u<<1|1;
if( t[ls].lr == t[ls].r && t[rs].lr ) t[u].lr = t[rs].lr;
else t[u].lr = t[ls].lr;
if( t[rs].rl == t[rs].l && t[ls].rl <= n ) t[u].rl = t[ls].rl;
else t[u].rl = t[rs].rl;
t[u].a = min(t[ls].a,t[rs].a);
t[u].a = min(t[u].a,Seg(min(t[ls].rl,t[rs].l),max(t[rs].lr,t[ls].r)));
}
void build(int u,int l,int r) {
t[u].l = l, t[u].r = r;
if( l == r ) {
t[u].lr = t[u].rl = l;
t[u].a = Seg(l,l);
return;
}
int mid = l+r>>1;
build(u<<1,l,mid), build(u<<1|1,mid+1,r);
up(u);
// printf("> %d %d: %d %d %d %d\n",l,r,t[u].lr,t[u].rl,t[u].a.l,t[u].a.r);
}
void modify(int u,int p,bool x) {
if( t[u].l == t[u].r ) {
if( x ) t[u].lr = 0, t[u].rl = n+1, t[u].a = Seg(n+1,0);
else t[u].lr = t[u].rl = t[u].l, t[u].a = Seg(t[u].l,t[u].l);
return;
}
int ls = u<<1, rs = ls|1;
modify( p<=t[ls].r?ls:rs ,p,x);
up(u);
}
signed main() {
// freopen("c.in","r",stdin);
// freopen("c.out","w",stdout);
read(n,m);
build(1,1,n);
while( m-- ) {
int op,x; read(op,x);
if( op == 1 ) {
Seg a = t[1].a;
if( a.l == 1 ) pos[x] = 1;
else if( a.r == n ) pos[x] = n;
else pos[x] = a.l+a.r>>1;
modify(1,pos[x],1);
write(pos[x]), putc(10);
} else modify(1,pos[x],0);
}
return ioclear();
}



