【题解】SDOI2021集训 R1 半夜
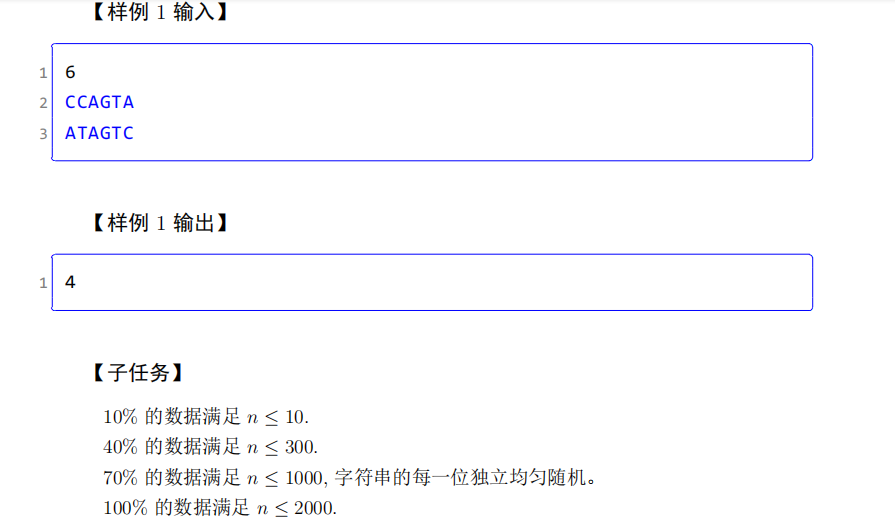
\(O(n^3)\)：对 \(XX\) 每个长度为 \(n\) 的字串与 \(Y\) 跑 LCS。设 \(f[i,j,k]\) 表示 \(X[i..j],Y[1..k]\) 的 LCS，暴力转移：\(f[i,j,k]=\max(f[i,j-1,k],f[i,j,k-1],[X[j]=Y[i]](f[i,j-1,k-1]+1))\)。
考虑两个性质：
\[f[i-1,j,k]>f[i-1,j-1,k]\Rightarrow f[i,j,k]>f[i,j-1,k]
\]
\[f[i-1,j,k-1]>f[i-1,j,k-1]\Rightarrow f[i,j,k]>f[i,j,k-1]
\]
证明没看懂，这里提供感性理解：
\(f[i-1,j,k]>f[i-1,j-1,k]\) 说明 \(X[j]\) 可以与 \(Y\) 中一个元素匹配，那么移动 \(i\) 对其他部分的影响相同，且不会影响它，那么 \(f[i,j,k]\) 仍 \(>f[i,j-1,k]\)，第二个同理。
通过这两个性质可以发现一定存在分割点 \(p[j,k],q[j,k]\) 使 \(f[i,j,k]=f[i,j-1,k]+[i>p[j,k]]=f[i,j,k-1]+[i<q[j,k]]\)，用 \(p[j,n]\) 就能 \(O(n^2)\) 递推出 \(f[i,i+n-1,n]\)。
注意这里 \(p,q\) 的两维与上两篇是反的，边界也不太相同。
考虑如何求 \(p,q\)。
设 \(F=f[i,j-1,k-1],P=p[j-1,k],Q=q[j,k-1]\)。分类讨论：
- \(X[j]\neq Y[k]\)
- \(P<Q\)
| \(i\) | \(P\) | \(Q\) | |
|---|---|---|---|
| \(f[i,j-1,k]\) | \(F+1\) | \(F+1\) | \(F\) |
| \(f[i,j,k-1]\) | \(F\) | \(F+1\) | \(F+1\) |
| \(f[i,j,k]\) | \(F+1\) | \(F+1\) | \(F+1\) |
其中 \(f[i,j,k]\) 的取值是根据最开始的暴力 DP 转移得到的，根据 \(f[i,j,k]\) 的取值就能得出 \(p[j,k]=Q,q[j,k]=P\)
其余三类也可以写出类似的表格，注意 \(X[j]=Y[k]\) 时 \(f[i,j,k]=f[i,j-1,k-1]+1\)，这里就不一一列出了。
代码异常简洁：
const int N = 4e3+5;
int n;
char a[N],b[N];
int m,ans,p[N][N],q[N][N];
signed main() {
scanf("%d%s%s",&n,a+1,b+1); m = n+n; memcpy(a+n+1,a+1,n);
For(j,1,m) p[j][0] = j;
For(j,1,m) For(k,1,n) {
int P = p[j][k-1], Q = q[j-1][k];
if( a[j] != b[k] && P > Q ) p[j][k] = P, q[j][k] = Q;
else p[j][k] = Q, q[j][k] = P;
}
For(i,1,n) {
int now = 0;
For(j,i,i+n-1) now += i>p[j][n];
ckmax(ans,now);
}
write(ans);
return iocl();
}
