【noip模拟】DP
11.17 追逐
第三次做了,然而还是花了 1.5h,不知道自己在干什么
记 \(s[u]\) 为 \(u\) 周围点的铁球数之和(不包括 \(u\))
设 \(f[u,i]\) 为从 \(u\) 的子树走到 \(u\)(\(u\) 不为起点),放了 \(i\) 个磁铁的最大铁球数,那么 \(f[u,i]=\max\{f[v,i],f[v,i-1]+s[u]-a[v]\}\)(从子树 \(v\) 走到 \(u\) 时点 \(v\) 已经走过了,不算追逐者多遇到的铁球)。枚举每个点为根 DP,时间复杂度 \(O(n^{2}v)\),期望得分 70pts(可以加上随机化,但效果不太好)
进一步思考,既然能 DP 出 \(f\),那么也应该能 DP 出类似的 \(g[u,i]\) 表示从 \(fa\) 走到 \(u\),只要将两条链拼起来就好了。\(u\) 这个点好像比较特殊,但仔细思考发现状态的定义保证了 \(u\) 不被算重,因此直接用 \(f[u,i]+g[v,m-i]\) 更新答案就好了
注意一些细节:\(f,g\) 需要做前缀 \(\max\)(可能用不了 \(m\) 个);需要把儿子顺序反过来再 DP 一次(走的顺序是从前面的儿子到 \(u\) 到后面的儿子)
10.21 连通性
比较套路的图计数,但考场上把约束转化为环,发现更 tm 难做了。。。
记 \([1,n-m]\) 为黑点,\((n-m,n]\) 为白点,Floyd 中 \(k\le n-m\) 相当于不以白点为中转点转移路径,因此每个连通块里的点对都能找到除了端点都为黑点的路径。
详细的说,全是白点的连通块必须是团;否则对于每个连通块,黑点的导出子图联通且每个白点至少与一个黑点连边
设 \(f[n,m]\) 表示 \(n,m\) 对应的答案,\(g[n]\) 为 \(n\) 个点无向联通图的个数,\(h[n]\) 为 \(n\) 个点无向图个数
\(g[n],h[n]\) 是图计数的经典套路:
考虑枚举 \(n\) 所在连通块大小 \(i\) 来转移 \(f[n,m]\)
- 全是白点:\(\displaystyle\sum_{i=1}^{m}f[n-i,m-i]\times{m-1\choose i-1}\)
- 有 \(j\) 个黑点:\(\displaystyle\sum_{i=1}^{m}\sum_{j=1}^{n-m}f[n-i-j,m-i]\times{m-1\choose i-1}{n-m\choose j}h[i]g[j](2^{j}-1)^{i}\)
10.18 邻面合并
很新颖的状压 DP
发现 \(m\le8\),可以对每行状压,问题在于如何把当前行的和上一行拼起来,发现需要知道每个矩形的宽度,普通状压难以胜任,那就用 \(1\) 表示一个矩形的开头,\(a_{i,j}\) 辅助判断 \(0\) 是空格子还是矩形上一点
以下是官方题解
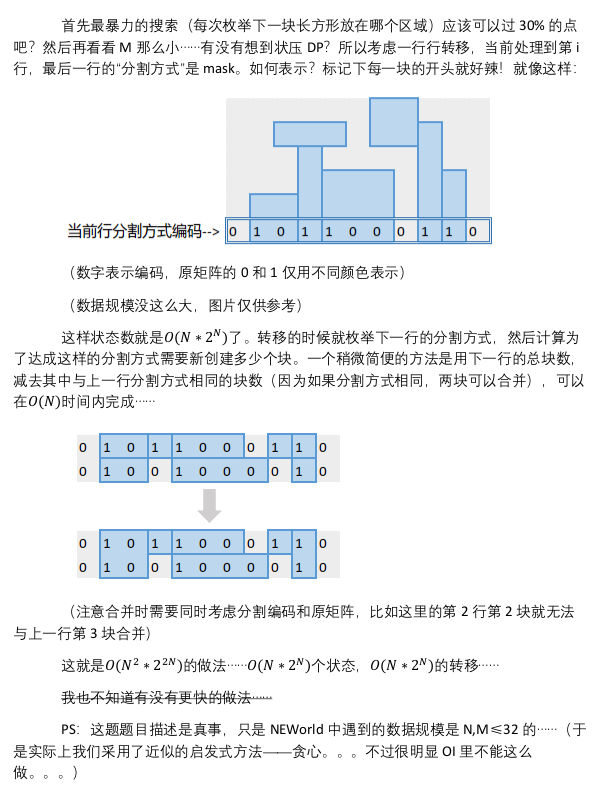
确切的说,时间复杂度是 \(O(nm2^{2m})\)。
code
const int N = 105, M = 8, inf = 0x3f3f3f3f;
int n,m,a[N][M];
int U,f[N][1<<M];
bool check(int i,int s) {
if( a[i][0] && !(s&1) ) return 0;
Rep(j,0,m, flg = 0) {
if( !a[i][j] && ((s>>j) & 1) ) return 0;
if( (s>>j) & 1 ) flg = 1;
if( !a[i][j] ) flg = 0;
else if( a[i][j] && !flg ) return 0;
}
return 1;
}
signed main() {
freopen("merging.in","r",stdin);
freopen("merging.out","w",stdout);
memset(f,0x3f,sizeof f);
read(n,m); U = (1<<m)-1;
For(i,1,n) Rep(j,0,m) read(a[i][j]);
f[0][0] = 0;
For(i,1,n) For(s,0,U) if( check(i,s) ) For(t,0,U) if( f[i-1][t] != inf ) {
int cnt = __builtin_popcount(s);
Rep(j,0,m) if( ((s>>j) & 1) && ((t>>j) & 1) ) {
// 以下是判两个矩形能不能拼起来
// 通过分别计算两行矩形的宽度可以避免分类讨论
bool flg = 1;
while( ++j < m ) {
if( !a[i][j] && !a[i-1][j] ) break;
else if( a[i][j] && a[i-1][j] ) {
if( ((s>>j)&1) && ((t>>j)&1) ) break;
else if( ((s>>j)&1) != ((t>>j)&1) ) { flg = 0; break; }
} else {
if( a[i][j] && !((s>>j)&1) ) flg = 0;
else if( a[i-1][j] && !((t>>j)&1) ) flg = 0;
break;
}
} --j;
cnt -= flg;
}
ckmin(f[i][s],f[i-1][t]+cnt);
}
write(*min_element(f[n],f[n]+U+1));
return ocl();
}
学长还讲过 \(O(nm3^{m+1})\) 的插头 DP 做法,但本人太弱没有听懂
10.17 S
考场上想到了这题,但记不清了,于是一直在想 kmp+栈贪心,连 \(a\cdots ab\cdots b,ab\) 都过不去。。。暑假也遇到过类似的问题,一是要记请原题的核心思想而不仅仅是做法,二是考场上不要老往原题上套,该自己想就自己想
考虑 kmp 预处理出 \(tr[i,c]\) 表示串 \(t\) 的前 \(i\) 位后接一个字符 \(c\) 的最长 border,然后 DP 就比较自然了。
设 \(f[i,j]\) 表示串 \(s\) 的第 \(i\) 位,与串 \(t\) 匹配的最长前缀是 \(j\) 的最小花费,转移时考虑 \(s_{i}\) 删不删:
注意滚动数组
10.16 Y
为了方便,令所有人都向右给
一个重要性质:如果没有人给 \(0\) 个球,那么等价于所有人都少给一个,这样最终一定有人给 \(0\) 个。显然这样不会漏掉某种情况,且相同的 \(B\) 只被计算了一次。
考虑枚举第一个给 \(0\) 球的位置 \(i\),\(i+1\) 的最终球数与 \(i\) 无关,可以破环成链后 DP。设 \(f[i,j]\) 为第 \(i\) 个人给了 \(j\) 个球的贡献,则 \(f[i,j]=\sum_{k}f[i-1,k]\times(a_i-j+k)\),时间复杂度 \(O(n^{2}a)\)。
40pts
const int N = 2e3+5, mod = 1e9+7;
int n,a[N];
LL ans,f[N][N];
signed main() {
freopen("y.in","r",stdin);
freopen("y.out","w",stdout);
read(n); Rep(i,0,n) read(a[i]); reverse(a,a+n);
Rep(i,0,n) {
memset(f,0,sizeof f);
For(j,i==n-1,a[(i+1)%n]) f[(i+1)%n][j] = a[(i+1)%n] - j;
Rep(j,i+2,n) For(k,0,a[j]) For(l,0,a[j-1])
(f[j][k] += (a[j]-k+l) * f[j-1][l]) %=mod;
Rep(j,i==n-1,i) For(k,1,a[j]) For(l,0,a[(j-1+n)%n])
(f[j][k] += (a[j]-k+l) * f[(j-1+n)%n][l]) %=mod;
For(j,0,a[(i-1+n)%n]) (ans += (a[i]+j) * f[(i-1+n)%n][j]) %=mod;
}
write(ans);
return ocl();
}
拆一下式子发现 \(f[i,j]\) 只与 \(\sum_{k}f[i-1,k],\sum_{k}f[i-1][k]\times k\) 有关,不需要枚举 \(k\),时间复杂度 \(O(na)\)
50pts
const int N = 2e3+5, mod = 1e9+7;
int n,a[N];
LL ans,f[N][N],s1[N],s2[N];
signed main() {
freopen("y.in","r",stdin);
freopen("y.out","w",stdout);
read(n); Rep(i,0,n) read(a[i]); reverse(a,a+n);
Rep(i,0,n) {
memset(f,0,sizeof f), mem(s1,0,n), mem(s2,0,n);
For(j,i==n-1,a[(i+1)%n])
f[(i+1)%n][j] = a[(i+1)%n] - j,
(s1[(i+1)%n] += f[(i+1)%n][j]) %=mod,
(s2[(i+1)%n] += f[(i+1)%n][j] * j) %=mod;
Rep(j,i+2,n) For(k,0,a[j])
(f[j][k] += (a[j]-k)*s1[j-1] + s2[j-1]) %=mod,
(s1[j] += f[j][k]) %=mod, (s2[j] += f[j][k] * k) %=mod;
Rep(j,i==n-1,i) For(k,1,a[j])
(f[j][k] += (a[j]-k)*s1[(j-1+n)%n] + s2[(j-1+n)%n]) %=mod,
(s1[j] += f[j][k]) %=mod, (s2[j] += f[j][k] * k) %=mod;
(ans += a[i]*s1[(i-1+n)%n] + s2[(i-1+n)%n]) %=mod;
}
write(ans);
return ocl();
}
答案只与 \(\sum_{j}f[i,j]\) 有关,而后者的转移也不需要枚举 \(j\),可以省掉第二维,时间复杂度 \(O(n^2)\)
80pts
const int N = 2e3+5, mod = 1e9+7, inv2 = 500000004, inv6 = 166666668;
int n,a[N];
LL ans,f[N],g[N];
LL s0(int l,int r) { return r-l+1; }
LL s1(int l,int r) { return (l+r) * (r-l+1ll) %mod * inv2 %mod; }
LL s2(int n) { return n>=0 ? n*(n+1ll)%mod*(2*n+1)%mod*inv6%mod : 0; }
LL s2(int l,int r) { return s2(r)-s2(l-1); }
signed main() {
freopen("y.in","r",stdin);
freopen("y.out","w",stdout);
read(n); Rep(i,0,n) read(a[i]); reverse(a,a+n);
Rep(i,0,n) {
mem(f,0,n), mem(g,0,n);
f[(i+1)%n] = (s0(i==n-1,a[(i+1)%n])*a[(i+1)%n] - s1(i==n-1,a[(i+1)%n])) %mod,
g[(i+1)%n] = (s1(i==n-1,a[(i+1)%n])*a[(i+1)%n] - s2(i==n-1,a[(i+1)%n])) %mod;
Rep(j,i+2,n)
f[j] = (s0(0,a[j])*a[j]%mod*f[j-1] - s1(0,a[j])*f[j-1] + s0(0,a[j])*g[j-1]) %mod,
g[j] = (s1(0,a[j])*a[j]%mod*f[j-1] - s2(0,a[j])*f[j-1] + s1(0,a[j])*g[j-1]) %mod;
Rep(j,i==n-1,i)
f[j] = (s0(1,a[j])*a[j]%mod*f[(j-1+n)%n] - s1(1,a[j])*f[(j-1+n)%n] + s0(1,a[j])*g[(j-1+n)%n]) %mod,
g[j] = (s1(1,a[j])*a[j]%mod*f[(j-1+n)%n] - s2(1,a[j])*f[(j-1+n)%n] + s1(1,a[j])*g[(j-1+n)%n]) %mod;
ans += (a[i]*f[(i-1+n)%n] + g[(i-1+n)%n]) %mod;
}
write((ans%mod+mod)%mod);
return ocl();
}
转移很像 \(2\times2\) 的矩阵乘法,把转移改写成矩乘形式,预处理前后缀的转移矩阵,时间复杂度 \(O(2^{3}n)\)
AC
const int N = 1e6+5, mod = 1e9+7, inv2 = 500000004, inv6 = 166666668;
int n,a[N];
LL ans;
struct Mat {
LL a[2][2];
Mat() { memset(a,0,sizeof a); }
LL* operator [] (int i) { return a[i]; }
} f[N],g[N];
Mat operator * (Mat x,Mat y) {
Mat res;
For(i,0,1) For(k,0,1) For(j,0,1) res[i][j] += x[i][k]*y[k][j];
For(i,0,1) For(j,0,1) res[i][j] %=mod;
return res;
}
LL s0(int l,int r) { return r-l+1; }
LL s1(int l,int r) { return (l+r) * (r-l+1ll) %mod * inv2 %mod; }
LL s2(int n) { return n>=0 ? n*(n+1ll)%mod*(2*n+1)%mod*inv6%mod : 0; }
LL s2(int l,int r) { return s2(r) - s2(l-1); }
signed main() {
freopen("y.in","r",stdin);
freopen("y.out","w",stdout);
read(n); For(i,1,n) read(a[i]); reverse(a+1,a+n+1);
f[0][0][0] = f[0][1][1] = g[n+1][0][0] = g[n+1][1][1] = 1;
For(i,1,n)
f[i][0][0] = (s0(1,a[i])*a[i]-s1(1,a[i]))%mod, f[i][1][0] = s0(1,a[i]),
f[i][0][1] = (s1(1,a[i])*a[i]-s2(1,a[i]))%mod, f[i][1][1] = s1(1,a[i]),
f[i] = f[i-1] * f[i];
rFor(i,n,1)
g[i][0][0] = (s0(0,a[i])*a[i]-s1(0,a[i]))%mod, g[i][1][0] = s0(0,a[i]),
g[i][0][1] = (s1(0,a[i])*a[i]-s2(0,a[i]))%mod, g[i][1][1] = s1(0,a[i]),
g[i] = g[i] * g[i+1];
For(i,1,n) {
Mat dp;
if( i < n )
dp[0][0] = (s0(0,a[i+1])*a[i+1] - s1(0,a[i+1])) %mod,
dp[0][1] = (s1(0,a[i+1])*a[i+1] - s2(0,a[i+1])) %mod,
dp = dp * g[i+2];
else dp[0][0] = dp[1][1] = 1;
dp = dp * f[i-1];
ans += (a[i] * dp[0][0] + dp[0][1]) %mod;
}
write((ans%mod+mod)%mod);
return ocl();
}
强烈建议写一下这题的所有做法,会对 DP 的边界和优化有更深的理解(注意本人不同代码中 \(f,g\) 的含义并不总是相同)
10.16 S
两个显然的结论:同色球的相对顺序不会改变;球的状态确定,交换次数也就确定了
根据结论一,只要能刻画出球的状态即可,比较显然的想法是区间 DP,但问题在于合并两个区间时如果端点颜色一样,需要知道从哪里移一个球过来,gg
因此考虑线性 DP,这样有两个好处:每次只要将一段前缀和一个球合并;这个球一定从后面移过来。
设 \(f[i,a,b,0/1/2]\) 为答案的前 \(i\) 个球,三种球分别有 \(a,b,i-a-b\) 个,第 \(i-1\) 个是哪种。转移有两部分:第 \(i-1\) 个球不能与第 \(i\) 个同色;第 \(i\) 个球在哪里(根据结论一,可以预处理出这个球原来的位置,根据三种球的数量也能算出有多少个原来在它后面的球被移到它前面,从而得出它现在的位置)
注意空间需要滚动数组
10.12 你猜是不是找规律
\(O(nk)\) 的暴力 DP 显然:设 \(f[i,j]\) 为前 \(i\) 个数交换不超过 \(j\) 次后合法的排列数,转移:\(f[i,j]=f[i-1,j]+(i-1)f[i-1,j-1]\)(\(i\) 要么放在原位,要么与前 \(i-1\) 个数中的一个交换)
显然应该重设状态,发现每次交换最多使两个数合法,因此合法排列最多有 \(2k\) 个数非法,设 \(f[i,j]\) 表示 \(i\) 个数错排,交换恰好 \(j\) 次后合法的排列数(错排是为了把这 \(i\) 个数放回原序列后一定不合法,也就不会算重)
初值:\(f[0,0]=1\)
转移:\(f[i,j]=(i-1)(f[i-2,j-1]+f[i-1,j-1])\)
答案:\(\sum_{i=0}^{2k}{n\choose i}\sum_{j=1}^{k}f[i,j]\)
注意这题空间 \(128\) MB,要么开 int 要么滚动数组
matrix
记号:
左区间:\([1,l_{i}]\);左区间同理
\(le[i]\) :在第 \(i\) 列结束的左区间数量
\(ri[i]\) :在第 \(i\) 列开始的右区间数量
每列最多放一个,这个条件可以用来按列转移,因此设 \(f[i,j]\) 表示前 \(i\) 列满足在 \(i-1\) 列前结束的左区间合法且 \(j\) 行的右区间合法的方案数(比较奇特)
转移:
有 \(i-j-le[i-1]\) 个空列,需要在 \(le[i]-le[i-1]\) 个左区间放 \(1\),排列数的含义就是把这些空列分配给这些左区间。



