计算机视觉课后作业4——多图拼接

一.实验内容：

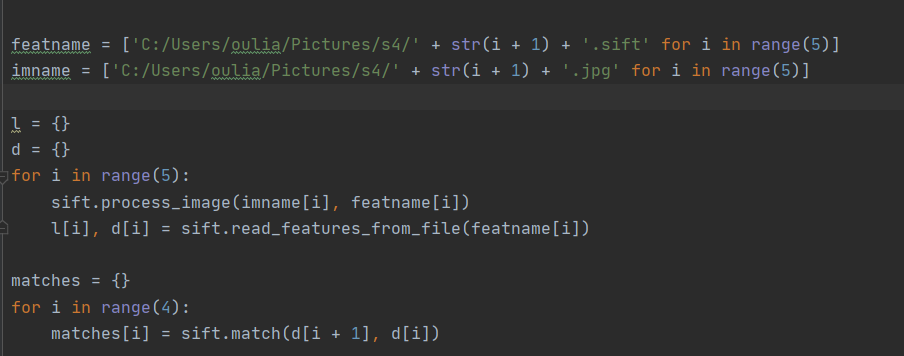
1.利用sift1算法和ransac算法实现全景图像拼接

2.进一步做平面图像和景深面复杂图像的多图拼接

二.实验环境：pycharm

三.实验原理：

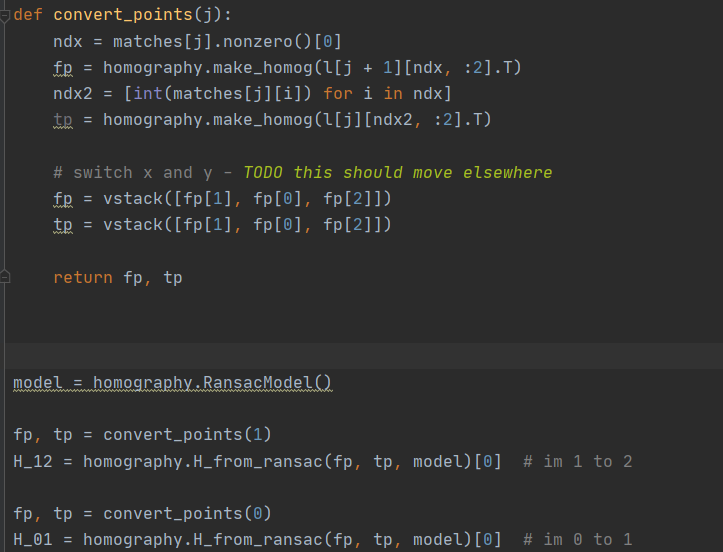
首先对于两张图片的简单拼接，只需找出两张图片中相似的至少四个点，计算一张图片可以变换到另一张图片的单应性变换矩阵，用这个矩阵把那张图片变换后放到另一张图片相应的位置，就是相当于把两张图片中定好的四个相似的点重合在一起。得到的新图片就实现了简单的全景拼接。

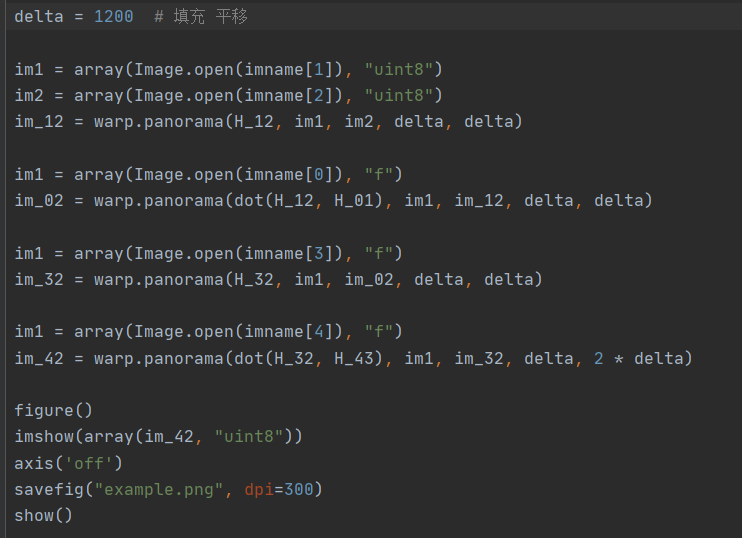
而对于多图拼接，在两张图片拼接的基础上，对算法进行循环，进行两两拼接。

1.SIFT算法：

SIFT算法是用来提取图像局部特征的经典算法，SIFT算法的实质是在不同的尺度空间上查找关键点(特征点)，并计算出关键点的方向。SIFT所查找到的关键点是一些十分突出，不会因光照，仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等。

用sift算法提取图像的特征点进行匹配，具体原理在实验二中已经论述。此处需要注意的问题是，sift算法特征匹配过程中可能出现错误的匹配信息，易产生位置估计失败的问题。因此，在实现全景图像拼接的时候，剔除这些错配点有很大的必要性。

2.RANSAC算法：

RANSAC算法是“RANdom SAmple Consensus（随机抽样一致）”的缩写。该方法是用来找到正确的模型来拟合带有噪声数据的迭代方法。它可以从一组包含“局外点”的观测数据集中，通过迭代方式估计数学模型的参数。其基本的思想是：数据中包含正确的点和噪声点，合理的模型应该能够在描述正确数据点的同时摒弃噪声点。

算法的基本假设是：

（1）数据由“局内点”组成，例如：数据的分布可以用一些模型参数来解释；
（2）“局外点”是不能适应该模型的数据；
（3）除此之外的数据属于噪声。

用RANSAC算法用一条直线来拟合直线：

假设观测数据中包含局内点和局外点，其中局内点近似的被直线所通过，而局外点远离于直线。简单的最小二乘法不能找适应于局内点的直线，原因是最小二乘法尽量去适应包括局外点在内的所有点，相反，RANSA能得出一个仅仅用局内点计算出模型，并且概率还足够高，但是不能保证结果一定正确。

RANSAC算法通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点，并用下述方法进行验证：
    1.有一个模型适应于假设的局内点，即所有的未知参数都能从假设的局内点计算得出。
    2.用1中得到的模型去测试所有的其它数据，如果某个点适用于估计的模型，认为它也是局内点。
    3.如果有足够多的点被归类为假设的局内点，那么估计的模型就足够合理。
    4.然后，用所有假设的局内点去重新估计模型，因为它仅仅被初始的假设局内点估计过。
    5.最后，通过估计局内点与模型的错误率来评估模型。
这个过程被重复执行固定的次数，每次产生的模型要么因为局内点太少而被舍弃，要么因为比现有的模型更好而被选用。

3.拼接图像：

使用RANSAC算法估计出图像间的单应性矩阵，之后需要将所有的图像扭曲到一个公共的平面上，通常，这里的公共平面为中心图像平面。由于此次实验的照片是站在原地旋转拍摄得到的，所以我们可以将中心图像左边或者右边的区域填充0，一边为扭曲的图像腾出空间。

四.实验过程（具体代码）：

1.sift特征匹配：