计算机视觉课后作业2——匹配地理标记图像

                                                             匹配地理标记图像

1.要求：

使用SIFT算法分别对多张图片进行特征描述子的提取，根据特征点的匹配结果对图片进行可视化分类和连线。

2.实验环境：

pycharm+graphviz图形库

3.SIFT算法的基本介绍：

SIFT算法也称为尺度不变特征变换，具有尺度不变性，可在图像中检测出关键点，是一种局部特征描述子。SIFT算法的实质是在不同的尺度空间上查找关键点，并计算出关键点的方向。SIFT特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关，所查找到的关键点是一些十分突出，不会因光照，仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等，对于光线、噪声、些微视角改变的容忍度相当高，因此它可以用于三维视角和噪声的可靠匹配。

4.SIFT算法的基本原理：

     4.1.兴趣点：也就是关键点，使用高斯差分函数来定位兴趣点

  

  

  SIFT算法基于一些判断标准，通过高斯滤波（高斯模糊）去除不稳定点。

  4.2.描述子：描述子在兴趣点的基础上，除了位置和尺度信息，还引入了参考方向。

         a.在每个像素点附近选取网格结构，把该网格按照梯度主方向进行旋转。

         b.在网格的每个子区域内计算图像梯度方向直方图。

         c.每个子区域的直方图拼接起来构成描述子向量。

  4.3.检测兴趣点：

        a.转换检测的图片的格式为.pgm,并且将兴趣点的信息写入文件

        b.从上面输出文件中，将特征读取到Numpy数组中的函数。

        c.特征可视化

  4.4.匹配描述子

  对于将一幅图像中的特征匹配到另一幅图像的特征，一种稳健的准则（同样是由Lowe提出的）是使用者两个特征距离和两个最匹配特征距离的比率。

5.SIFT算法的步骤：

   5.1. 尺度空间极值检测：搜索所有尺度上的图像位置。通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点。

   5.2. 关键点定位：在每个候选的位置上，通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度。

   5.3. 方向确定：基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换，从而提供对于这些变换的不变性。

   5.4. 关键点描述：在每个关键点周围的邻域内，在选定的尺度上测量图像局部的梯度。这些梯度被变换成一种表示，这种表示允许比较大的局部形状的变形和光照变化。

6.实验代码：

 sift.py文件

# -*- coding: utf-8 -*-
import json
import os
import urllib

from numpy import zeros
from pylab import *
from PIL import Image
from PCV.localdescriptors import sift
from PCV.tools import imtools
import pydot

if __name__ == '__main__':
    download_path = "C:/Users/oulia/Pictures/shu"
    path = "C:/Users/oulia/Pictures/shu"

    imlist = imtools.get_imlist(download_path)
    nbr_images = len(imlist)

    featlist = [imname[:-3] + 'sift' for imname in imlist]
    for i, imname in enumerate(imlist):
        sift.process_image(imname, featlist[i])

    matchscores = zeros((nbr_images, nbr_images))

    for i in range(nbr_images):
        for j in range(i, nbr_images):  # only compute upper triangle
            print('comparing ', imlist[i], imlist[j])
            l1, d1 = sift.read_features_from_file(featlist[i])
            l2, d2 = sift.read_features_from_file(featlist[j])
            matches = sift.match_twosided(d1, d2)
            nbr_matches = sum(matches > 0)
            print('number of matches = ', nbr_matches)
            matchscores[i, j] = nbr_matches

    # copy values
    for i in range(nbr_images):
        for j in range(i + 1, nbr_images):  # no need to copy diagonal
            matchscores[j, i] = matchscores[i, j]

    # 可视化

    threshold = 20  # min number of matches needed to create link 创建链接所需匹配的最小数量

    g = pydot.Dot(graph_type='graph')  # don't want the default directed graph

    for i in range(nbr_images):
        for j in range(i + 1, nbr_images):
            if matchscores[i, j] > threshold:
                # first image in pair
                im = Image.open(imlist[i])
                im.thumbnail((100, 100))
                filename = path + str(i) + '.jpg'
                im.save(filename)  # need temporary files of the right size
                g.add_node(pydot.Node(str(i), fontcolor='transparent', shape='rectangle', image=filename))

                # second image in pair
                im = Image.open(imlist[j])
                im.thumbnail((100, 100))
                filename = path + str(j) + '.jpg'
                im.save(filename)  # need temporary files of the right size
                g.add_node(pydot.Node(str(j), fontcolor='transparent', shape='rectangle', image=filename))

                g.add_edge(pydot.Edge(str(i), str(j)))
    g.write_jpg('22.jpg')

 

7.实验结果和分析：

   运行后C:/Users/oulia/Pictures的图片以及.sift文件

  

  7.1.当创建链接所需匹配的最小数量为2时：

 

  代码运行部分结果：

  comparing C:/Users/oulia/Pictures\a1.jpg C:/Users/oulia/Pictures\b.jpg
  number of matches = 3

  comparing C:/Users/oulia/Pictures\b1.jpg C:/Users/oulia/Pictures\b1.jpg
  number of matches = 3656
  comparing C:/Users/oulia/Pictures\b1.jpg C:/Users/oulia/Pictures\c.jpg
  number of matches = 0
  comparing C:/Users/oulia/Pictures\b1.jpg C:/Users/oulia/Pictures\c1.jpg
  number of matches = 1
  comparing C:/Users/oulia/Pictures\b1.jpg C:/Users/oulia/Pictures\c2.jpg
  number of matches = 0
  comparing C:/Users/oulia/Pictures\b1.jpg C:/Users/oulia/Pictures\c3.jpg
  number of matches = 2

  通过对代码运行结果分析可知，图片b1和图片c,c1,c2的匹配点数都小于2，所以在图片上应该是没有连线的；特别注意的是，图片a1和图片b的匹配点数为2，正好大于我们设定的连线最小匹配点数，但是他们    二者很明显拍的不是同一个建筑物，这个连线是不应该存在的，这要求我们必须重新调整thredshold的值。（如下图）

   

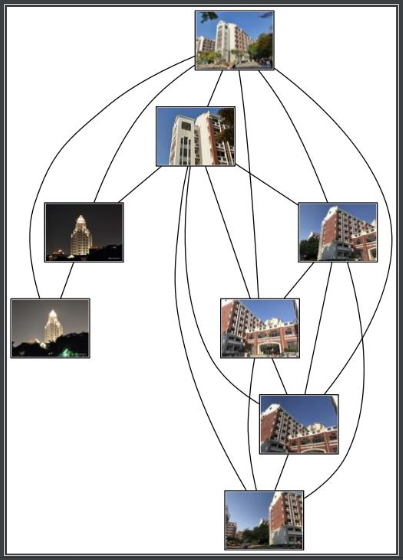
  7.2.当把创建链接所需匹配的最小数量调整为20时：

   

   代码部分运行结果：

   comparing C:/Users/oulia/Pictures\a.jpg C:/Users/oulia/Pictures\a1.jpg
   number of matches = 6
   comparing C:/Users/oulia/Pictures\a.jpg C:/Users/oulia/Pictures\b.jpg
   number of matches = 11

   从运行结果我们看到，图片a和图片a1属于同一建筑物，但是由于图片原因，造成匹配的特征点较少。而图片a和图片b不属于同一建筑物，但是他们之间的特征点要多于a和a1,导致单纯靠调整threshold的值可     能无法处理类似情况。比如当我们把创建链接所需的最小匹配数量调到20，试图避免不同建筑物图片间的误连时，虽然图片a和图片b的连线没有了，但也意外误伤了图片a和图片a1，导致他们之间不能连线，     故最终结果中没有了这组图片。（如下图）

   

   从这两个结果对比，我们可以看出，对于创建链接所需的最小匹配数量这个变量，sift算法对于比较不同的图片需要由程序员去判断和测试其具体值，无法一概论之；如果图片属于同一建筑物但是因为一些光       线和角度问题导致特征匹配点较少的时候，也可能不能很好的匹配起来。虽然sift算法对图片的包容度很高，但是一些硬性的要求还是必不可少，从某一方面来说对图像的拍摄质量也有一定的要求，这可能也       是SIFT算法的美中不足之一。

   面对这种情况，可能还需要额外设置SIFT算法一些其他的变量或者其他算法来进行辅助判断。

  7.3.花草图像测试：

  

   运行结果：

   comparing C:/Users/oulia/Pictures/shu\s.jpg C:/Users/oulia/Pictures/shu\s.jpg
   number of matches = 6625
   comparing C:/Users/oulia/Pictures/shu\s.jpg C:/Users/oulia/Pictures/shu\s1.jpg
   number of matches = 0
   comparing C:/Users/oulia/Pictures/shu\s.jpg C:/Users/oulia/Pictures/shu\s2.jpg
   number of matches = 0
   comparing C:/Users/oulia/Pictures/shu\s1.jpg C:/Users/oulia/Pictures/shu\s1.jpg
   number of matches = 3770
   comparing C:/Users/oulia/Pictures/shu\s1.jpg C:/Users/oulia/Pictures/shu\s2.jpg
   number of matches = 0
   comparing C:/Users/oulia/Pictures/shu\s2.jpg C:/Users/oulia/Pictures/shu\s2.jpg
   number of matches = 4362

   在做花草的图像匹配的时候，我使用的三张图片属于三个不同的花草丛，但是从图片来看其实有很多相似点。而出乎我的意料的是，运行结果显示他们三张图片之间的特征匹配点均为0，这一结果令人疑惑。

   查阅资料后，判断可能是因为花草纹理不明显，缺少容易识别的边角，以至于sift算法不能找到有效的特征匹配点。

8.实验中遇到的问题及解决方法：

   1.刚开始没有下载graphviz图形库的插件，导致pydot运行不了，报错找不到路径。后来百度下载了graphviz-2.38.msi，并且把路径添加到系统变量path中，问题解决。

   2.再次运行过程中报错——数组越界，尝试将图片缩小到100kb左右，就可以运行。通过这个我们可以得出，用于sift算法的图片不宜过大，其一是可能导致程序报错，其二运行时间也容易过长。

   3.程序中涉及vlfeat库的使用，我使用的是助教已经提供的版本运行无错。如果出现错误的话，可考虑可能是vlfeat库版本的问题。

9.尚存的不足：

   这次实验我拍摄的几组图片中，有的图片由于角度问题导致匹配点较少。如上文实验结果与分析中所提到的，为了避免实验使用的图片的多余误连，导致其中本应该连接的两张图片因为拍摄时没注意角度的问题造成匹配点较少而不得不被忽略掉，所以得到的实验结果还不是最佳的。