计算机视觉课后作业1——图像处理基础
刚刚开始接触计算机视觉的课程,此次完成图像处理基础部分的内容,并且将其中的直方图,高斯滤波和直方图均衡化的实验结果写在该博客。
环境:Python+opencv
软件:PyCharm 2020.1.1
目录
1 直方图
1.1 基本原理
1.2 代码
1.3 实验截图
2 直方图均衡化
2.1 基本原理
2.2 代码
2.3 实验截图
3 高斯滤波(高斯模糊)
3.1 基本原理
3.2 代码
3.3 实验截图
1 直方图
1.1 基本原理
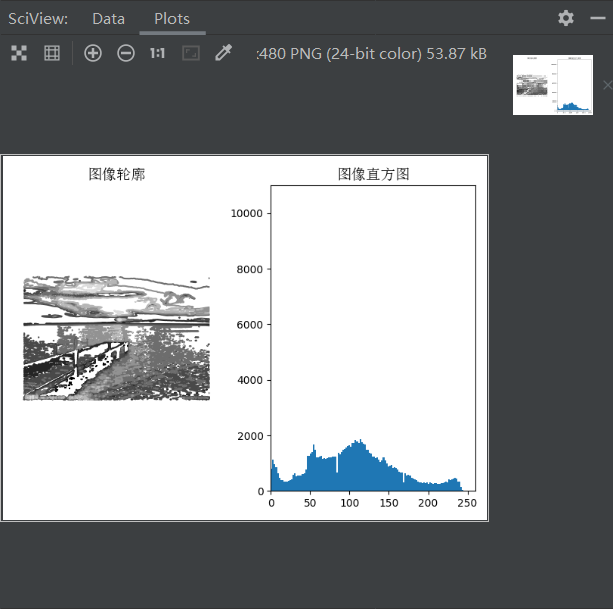
图像的直方图反映了一幅图像的像素分布情况。横坐标代表像素的种类,纵坐标代表每一种像素值在图像中的像素总数或者占所有像素个数的百分比,能够很直观的展示出图像中各个像素值占比的多少。
我们一般用到的直方图都是灰度直方图,其中横坐标是图像的灰度级(0-255),纵坐标则是该灰度级出现的频率或个数。
通过一幅图像的亮暗情况就可以判断出其直方图的大致分布情况,较暗的图像的直方图像素分布聚集在左侧,较亮的图像直方图像素分布聚集在右侧。
1.2 代码
注意:
<1>用到了PIL库中的Image模块,用来打开本地图片。PIL(Python Imaging Library)是一个非常好用的图像处理库,但新版的Python不支持PIL,而是使用Pillow(也是第三方库)。
<2>pylab 模块是进行二维,三维数据绘制的工具模块,由于 pylab是matplotlib中的一个模块 所以我们直接安装matplotlib库就可以对它进行调用。
<3>在默认状态下,matplotlb无法在图表中使用中文,在此我们使用matplotlib的字体管理器matplotlib.Font_manager来指定字体文件。
from PIL import Image
from pylab import *
from matplotlib.font_manager import FontProperties# 添加中文字体支持
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)# 指定字体文件——中文
im = array(Image.open('D:\\MATLAB\\bin\\fj.jpg').convert('L')) # 打开图像,并转成灰度图
figure()
subplot(121)
gray()
contour(im, origin='image')#在原点左上角显示轮廓图像
axis('equal')#x轴和y轴单位长度一致
axis('off')#关闭坐标轴线
title(u'图像轮廓', fontproperties=font)
subplot(122)
hist(im.flatten(), 128)#绘制图像灰度直方图
title(u'图像直方图', fontproperties=font)
plt.xlim([0,260])
plt.ylim([0,11000])
show()
1.3 实验截图
2 直方图均衡化
2.1 基本原理
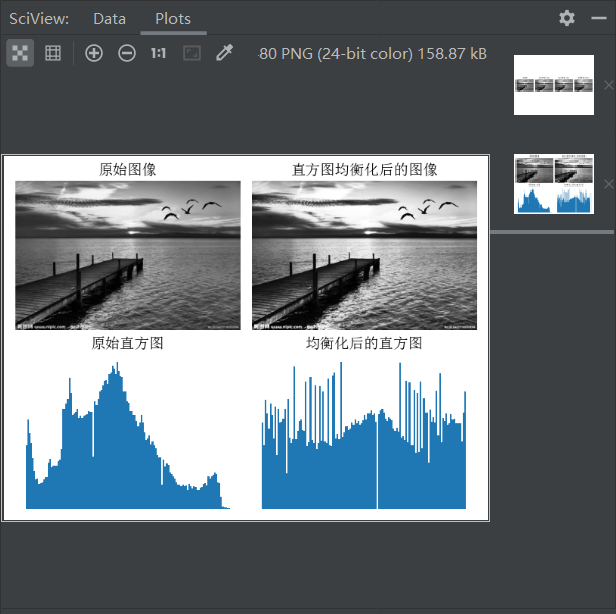
对于随便一张图来说,较暗图像的灰度直方图的分量(灰度级)集中在灰度较低的一端;而较亮图像的灰度直方图的分量则偏向于灰度较高的一端。但是有时候太暗或者太亮都不能满足我们的需求。
我们如果想要获得对比度更强,细节更清晰的图像,我们应该如何操作图像的像素矩阵呢?答案是直方图的均衡化。
直方图均衡化利用对像素值的变换,使图像的灰度直方图较为平均地覆盖整个灰度的取值范围(0-255),对在图像中像素个数多的灰度值进行展宽,而对像素个数少的灰度值进行归并,从而增大图像的对比度,使图像清晰,同时图像的细节更为丰富。
具体的操作方法:对原始图像的像素灰度做某种映射变换, 使变换后图像灰度的概率密度呈均匀分布。
数学原理:
设原始图像在(x,y)处的灰度为f,而改变后的图像为g,则对图像增强的方法可表述为将在(x,y)处的灰度f映射为g。在灰度直方图均衡化处理中对图像的映射函数可定义为:g = EQ (f),这个映射函数EQ(f)必须满足两个条件(其中L为图像的灰度级数):
(1)EQ(f)在0≤f≤L-1范围内是一个单值单增函数。这是为了保证增强处理没有打乱原始图像的灰度排列次序,原图各灰度级在变换后仍保持从黑到白(或从白到黑)的排列。
(2)对于0≤f≤L-1有0≤g≤L-1,这个条件保证了变换前后灰度值动态范围的一致性。
累积分布函数即可以满足上述两个条件,并且通过该函数可以完成将原图像f的分布转换成g的均匀分布。此时的直方图均衡化映射函数为:
gk = EQ(fk) = (ni/n) = pf(fi) ,
(k=0,1,2,……,L-1)
上述求和区间为0到k,根据该方程可以由源图像的各像素灰度值直接得到直方图均衡化后各像素的灰度值。在实际处理变换时,一般先对原始图像的灰度情况进行统计分析,并计算出原始直方图分布,然后根据计算出的累计直方图分布求出fk到gk的灰度映射关系。在重复上述步骤得到源图像所有灰度级到目标图像灰度级的映射关系后,按照这个映射关系对源图像各点像素进行灰度转换,即可完成对源图的直方图均衡化。
2.2 代码
注意:
运行以下代码需要导入PCV库。我自己在导入PCV库的时候出现了安装成功但是在PyCharm中仍然不能找到的情况,百度资料看到可能是虚拟项目环境和基本环境的冲突。
解决办法:把安装成功的PCV库复制到虚拟项目环境的专门存放各种库的文件夹中。
from PIL import Image
from pylab import *
from PCV.tools import imtools
# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)
im = array(Image.open('D:\\MATLAB\\bin\\fj.jpg').convert('L')) # 打开图像,并转成灰度图像
#im = array(Image.open('../data/AquaTermi_lowcontrast.JPG').convert('L'))
im2, cdf = imtools.histeq(im)#直方图均衡化函数
figure()
subplot(2, 2, 1)
axis('off')
gray()
title(u'原始图像', fontproperties=font)
imshow(im)
subplot(2, 2, 2)
axis('off')
title(u'直方图均衡化后的图像', fontproperties=font)
imshow(im2)
subplot(2, 2, 3)
axis('off')
title(u'原始直方图', fontproperties=font)
hist(im.flatten(), 128, density=True)#直方图绘制
subplot(2, 2, 4)
axis('off')
title(u'均衡化后的直方图', fontproperties=font)
hist(im2.flatten(), 128, density=True)
show()
2.3 实验截图
3 高斯滤波(高斯模糊)
3.1 基本原理
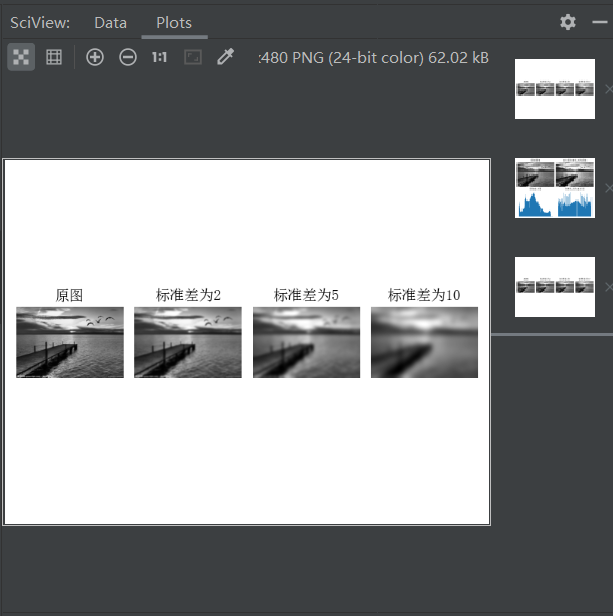
高斯滤波包含许多种,包括低通、带通和高通等。我们通常说的高斯滤波,其实指的是高斯模糊,是一种高斯低通滤波 ,其过滤掉图像高频成分(图像细节部分),保留图像低频成分(图像平滑区域),所以对图像进行 ‘高斯模糊’ 后,图像会变得模糊。
那如何进行模糊呢?
所有的图像操作以及变换都要通过对图像的像素矩阵进行相应操作来得到。所谓的模糊其实就是将图像中每个像素值进行重置(比如加权平均)的过程。通过对每一像素值的操作,在数值上,实现了一种"平滑化",像素之间的差别减小。在图形上,就相当于产生"模糊"效果。
加权平均要如何做到呢?
在图形上,正态分布是一种钟形曲线,越接近中心,取值越大,越远离中心,取值越小。
计算平均值的时候,我们只需要将"中心点"作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权平均值,以此类推。
3.2 代码
from PIL import Image
from pylab import *
from scipy.ndimage import filters
# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)
#im = array(Image.open('board.jpeg'))
im = array(Image.open('D:\\MATLAB\\bin\\fj.jpg').convert('L'))
figure()
gray()
axis('off')
subplot(1, 4, 1)
axis('off')
title(u'原图', fontproperties=font)
imshow(im)
for bi, blur in enumerate([2, 5, 10]):
im2 = zeros(im.shape)
im2 = filters.gaussian_filter(im, blur)
im2 = np.uint8(im2)
imNum=str(blur)
subplot(1, 4, 2 + bi)
axis('off')
title(u'标准差为'+imNum, fontproperties=font)
imshow(im2)
show()
3.3 实验截图
注意:
#如果是彩色图像,则分别对三个通道进行模糊
#for bi, blur in enumerate([2, 5, 10]):
# im2 = zeros(im.shape)
# for i in range(3):
# im2[:, :, i] = filters.gaussian_filter(im[:, :, i], blur)
# im2 = np.uint8(im2)
# subplot(1, 4, 2 + bi)
# axis('off')
# imshow(im2)
小白还在继续学习中!



