我眼中的机器学习(四) 快速寻找最优解

快速寻找最优解 -基础知识

通过上文,  我们知道了, 如果盲目使用随机算法或者遍历算法寻找最优解的话,  需要计算的空间将会太大. 为了能够让大家直观的感受一下实际应用的计算量, 我这里再举个例子, 1997年5月11日 IBM的深蓝AI战胜卡国际象棋名家斯帕罗夫. 我们知道 围棋的棋盘是19路总共361格, 如果计算机需要计算10步则需要计算的状态数量为361^10 = 37589973457545958193355601 个,  而前文我们提到的当步长为0.01时需要计算的状态数量为160000, 耗时约5秒, 而刚才提到的10步需要的计算量约为上文160000的 234937334109662238708倍. 

 

不难看出, 如果不使用一定的优化技巧, 使用暴力穷举来计算实际任务, 性能上将很容量成为瓶颈.

 

相对遍历或者穷举的方法， 梯度下降法（gradient descent ) 就是这样一种又快又准原理简单又容易实现的优化算法

 

所谓的梯度下降法就是让数学模型的参数(coefficient)沿着梯度的负方向进行快速迭代下降的过程， 该过程会一直迭代下去直到误差的范围符合用户的要求（成功创建模型）或者迭代次数达到上限时（失败）。

 

在正式介绍梯度下降算法之前， 本章先梳理一下梯度下降法会涉及到的基本概念

 

导数通常描述的是在只有一个自变量（一维）的函数空间内的某一点随着函数自变量变化时，函数本身的变化率（敏感程度）。导数的计算结果为一个标量（也就是一个数值）， 值越大， 单位长度的自变量变化带来的影响越大。直观的几何意思是函数在某一点的斜率。

 

当函数有多个自变量时（多元函数也叫多维函数）， 由于求导可以针对不同的自变量进行， 所以针对只有某个自变量进行变化的情况下求解的导数被称为偏导数。偏导数描述的是函数仅沿着坐标轴的某个方向进行变化时的函数变化率。

 

既然函数可以沿着坐标轴的某个方向进行求导， 那么自然也可以对沿着其它方向变化的函数进行求导（比如沿着与X轴成45度夹角的方向）， 在这个情况下求出来的导数我们称之为方向导数。 也就是说方向导数为多元多项式中（比如二元二次函数）某个点沿着某个向量方向进行求导后得到的值。（二元函数的自变量可以沿着[x,y]方向变化， 三元函数则可以沿[x,y,z]方向进行求导）

 

 

梯度为多元函数的偏导数组成的一个向量， 是一维导数在高维空间的推广（generalization)。 同样描述的是函数随着自变量进行变化时的变化率， 只是这个时候的自变量由一维（一个）变成了多维（多个自变量）。 沿着梯度方向进行求导时， 导数值最大， 也就是说函数在某个点沿着梯度方向变化时， 函数的值变化最快。

 

 

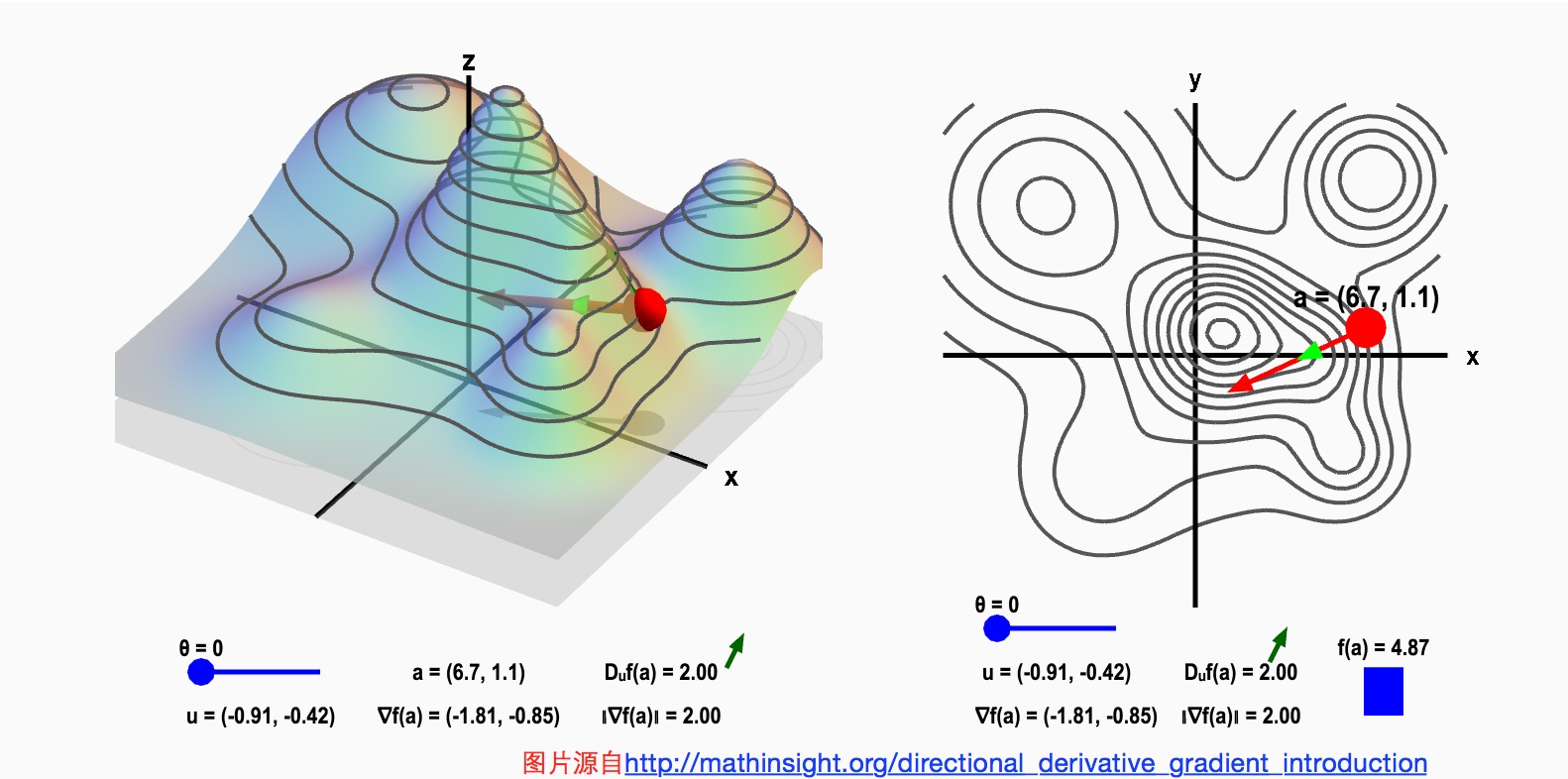
如下图所示， 左边的山是由函数f(x,y) 代表高度的情况下绘制出来的， 右边是这座山在二维平面的投影形成的等高线图。 右图中的红点可以沿着任意方向前进， 但是我们可以发现不同方向的高度变化是不一样的。 红点的箭头方向是梯度方向， 也是高度变化最剧烈的方向。

 

 

 

再如下图为一个二元二次函数 f(x,y) = −(cos²x + cos²y)²

图中的X，Y轴组成的平面上的红色箭头的方向 就是梯度的方向， 箭头的长度由函数在这个点上沿梯度方向求导计算出来的。

 

总结一下： 

导数是一个数值， 代表了函数在某个点的变化率。

梯度一个特殊的方向，因为它的方向是由函数在某个点的偏导数决定的 

 

知道了梯度的相关概念， 我们就直接来说说简单版的梯度下降算法（也叫 最速下降法 Gradient descent）

 

(1)首先对于任意一个函数， 我们都可以随机选择一个点作为我们的起始点X_0

(2)为了保证函数F（X）在朝某个方向移动 （单位步长）距离时 ，使函数值变的尽可能的小， 我们需要沿着梯度负方向的进行移动.  沿着梯度方向移动了一定长度后， 我们得到了点X_1与F(X_1).  

注意：只有在移动的距离足够小时， 我们才能保证移动后的点X_1的函数值F(X_1) 小于F(X_0).  因为导数针对的是某个点来计算的, 不同点的导数不一样, 所以步长不宜设的太长。

(3) 计算F(X_1)与F(X_0)的差值， 判断单位步长的移动带来的函数值的变化是否已经小于一个我们预设的， 非常小的一个值。

如果小于的话， 那就不需要再移动了， 因为继续移动的话函数值F（X）的变化也只会是非常小的。

如果本次移动带来的函数值变化非常大， 则说明算法还有进一步迭代的必要。则重复第二步， 和第三步

 

 

 

 

接着我们来说说一个实例

因为例子比较简单, 我们在应用梯度算法之前先使用在高中学过的令导数等于0计算驻点（极值点）的方法

求

$$ f(x) = x^{^4}-3x^{^3}+2 $$

的最小值

$$f'(x) = 4x^3-9x^2 =x^2(4x-9)$$

令f'(x)=0 可得驻点 $$x_1=0, x_2=2.25$$

将驻点代回方程 可得 最大值2 与最小值 -6.54296875

 

将刚才说的算法写成PYTHON脚本

# -*- coding: cp936 -*-
xOld = 0
xNew = 1 # The algorithm starts at x=6
moveDistance = 0.01 # step size
precision = 0.00001
def evaluateEquation(x):
    """计算原函数在自变量为x时的值"""
    return x**4-3*x**3+2
def evaluateGradient(x):
    """计算梯度向量"""
    return 4 * x**3 - 9 * x**2
step=0
while abs(evaluateEquation(xNew) - evaluateEquation(xOld)) > precision:
    step+=1
    xOld = xNew
    xNew = xOld - moveDistance * evaluateGradient(xNew)
    print "step",step,"xold=",xOld, "xnew=",xNew
print("Local minimum occurs at ", xNew, "with minimum value",evaluateEquation(xNew))
print "step",step

 

　　

 

 

运行后得到

>>>
step 1 xold= 1 xnew= 1.05
step 2 xold= 1.05 xnew= 1.10292
step 3 xold= 1.10292 xnew= 1.1587338169
step 4 xold= 1.1587338169 xnew= 1.21734197218
step 5 xold= 1.21734197218 xnew= 1.27855469659
step 6 xold= 1.27855469659 xnew= 1.34207564416
step 7 xold= 1.34207564416 xnew= 1.40748858095
step 8 xold= 1.40748858095 xnew= 1.47424999816
step 9 xold= 1.47424999816 xnew= 1.54169100548
step 10 xold= 1.54169100548 xnew= 1.60903167429
step 11 xold= 1.60903167429 xnew= 1.67540991642
step 12 xold= 1.67540991642 xnew= 1.73992485396
step 13 xold= 1.73992485396 xnew= 1.80169165901
step 14 xold= 1.80169165901 xnew= 1.85990167873
step 15 xold= 1.85990167873 xnew= 1.91387933776
step 16 xold= 1.91387933776 xnew= 1.96312685144
step 17 xold= 1.96312685144 xnew= 2.00734969025
step 18 xold= 2.00734969025 xnew= 2.04645960885
step 19 xold= 2.04645960885 xnew= 2.08055667019
step 20 xold= 2.08055667019 xnew= 2.10989555269
step 21 xold= 2.10989555269 xnew= 2.13484344301
step 22 xold= 2.13484344301 xnew= 2.15583674372
step 23 xold= 2.15583674372 xnew= 2.17334219049
step 24 xold= 2.17334219049 xnew= 2.1878256603
step 25 xold= 2.1878256603 xnew= 2.19972976112
step 26 xold= 2.19972976112 xnew= 2.20945968856
step 27 xold= 2.20945968856 xnew= 2.21737593374
step 28 xold= 2.21737593374 xnew= 2.22379211672
step 29 xold= 2.22379211672 xnew= 2.22897629956
step 30 xold= 2.22897629956 xnew= 2.23315441132
step 31 xold= 2.23315441132 xnew= 2.23651475494
step 32 xold= 2.23651475494 xnew= 2.23921288183
step 33 xold= 2.23921288183 xnew= 2.24137637832
step 34 xold= 2.24137637832 xnew= 2.24310930133
step 35 xold= 2.24310930133 xnew= 2.24449613419
step 36 xold= 2.24449613419 xnew= 2.24560522103
step 37 xold= 2.24560522103 xnew= 2.24649169063
step 38 xold= 2.24649169063 xnew= 2.24719990952
step 39 xold= 2.24719990952 xnew= 2.24776551743
step 40 xold= 2.24776551743 xnew= 2.24821710187
step 41 xold= 2.24821710187 xnew= 2.2485775668
step 42 xold= 2.2485775668 xnew= 2.24886524544
('Local minimum occurs at ', 2.2488652454412037, 'with minimum value', -6.542955721127889)
step 42

 

 

可以看到脚本进行了42次迭代后, 得到了最小值-6.54295572 (x=2.248) 与使用手工计算出来的最小值-6.54296875 的误差为0.00001303

 

那么现在你心中的疑问可能是

1.既然令导数为零可以直接求解, 为什么不直接让电脑计算令导数为零的方程式

答案是:  答案在前两篇的文章"我眼中的机器学习(二)" 中已经提过了, 当样本数据中有噪点时, 或者不可解时, 标准解方程的方式无用.

当然基于矩阵思想的最小二乘法通过计算高维空间中的一个向量在低维子空间的投影也是可以求解出误差最小的解的, 但是计算一个矩阵的逆是相当耗费时间的, 所以许多时候我们会更倾向于使用计算量并不算大的常规的最优化算法--比如梯度下降, 牛顿法等.

 

2.如何为梯度下降算法选择合适的步长, 多大的步长变化是最有效率的

关于这一点我会在下一章进一步说明.

 

 

 

 

 

 

 

http://mathinsight.org/directional_derivative_gradient_introduction

Nykamp DQ, “Directional derivative on a mountain.” From Math Insight. http://mathinsight.org/applet/directional_derivative_mountain

Keywords: directional derivative