链表递归题型
递归的定义
在定义一个过程或函数时出现调用本过程或本函数的成分,称之为递归。若调用自身,称之为直接递归。若过程或函数p调用过程或函数q,而q又调用p,称之为间接递归。
递归算法的设计
递归的求解过程均有这样的特征:先将整个问题划分为若干个子问题,通过分别求解子问题,最后获得整个问题的解。而这些子问题具有与原问题相同的求解方法,于是可以再将它们划分成若干个子问题,分别求解,如此反复进行,直到不能再划分成子问题,或已经可以求解为止。这种自上而下将问题分解、求解,再自上而下引用、合并,求出最后解答的过程称为递归求解过程,这是一种分而治之的算法设计方法。
简单递归算法设计方法:

例题
有一个不带表头节点的单链表,其节点类型如下:
typedef struct NodeType
{
ElemType data;
struct NodeType *next;
}NodeType;
设计如下递归算法:
1 求以h为首指针的单链表的节点个数。
2 正向显示以h为首指针的单链表的所有节点值。
3 反向显示以h为首指针的单链表的所有节点值。
4 删除以h为首指针的单链表中值为x的第一个节点。
5 删除以h为首指针的单链表中值为x的所有节点。
6 输出以h为首指针的单链表中最大节点值。
7 输出以h为首指针的单链表中最小节点值。
8 删除并释放以h为首指针的单链表中所有节点。
解:设h为不带头节点的单链表(含n个节点),如图所示,h->next 也是一个不带头节点的单链表(含n-1个节点),两者除了相差一个节点外,其他都是相似的。

1 求以h为首指针的单链表的节点个数
设count(h)用于计算单链表h的结点个数,其递归模型如下:
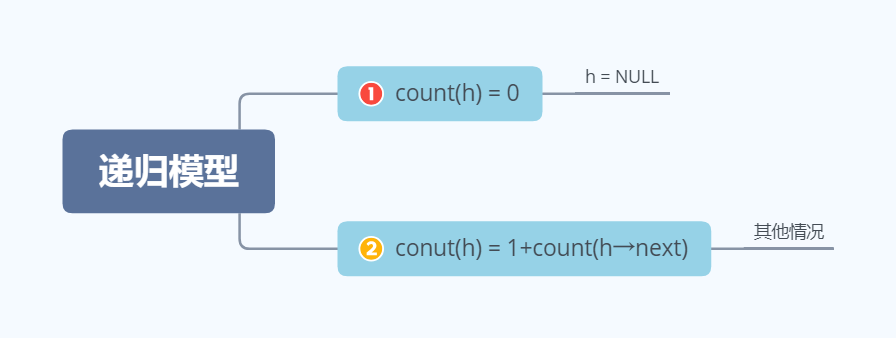
对于的递归算法如下:
int count(NodeType *h)
{
if(h==NULL)
return 0;
else
return (1+count(h->next));
}
2 正向显示以h为首指针的单链表的所有节点值
设traverse(h)用于正向扫描单链表h,其递归模型如下:
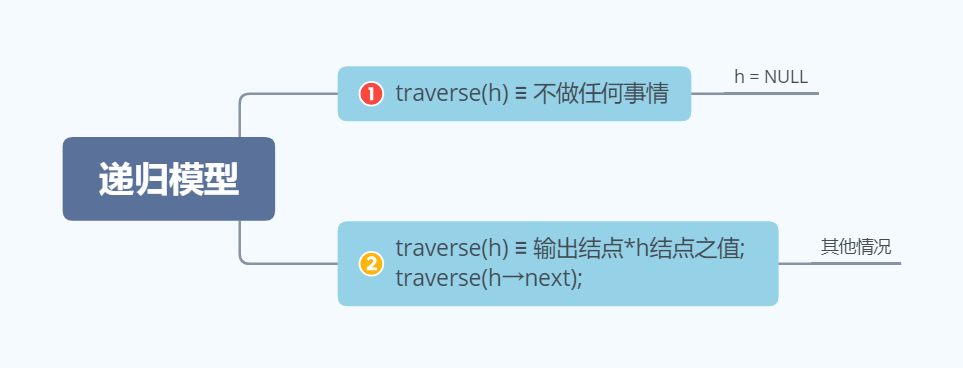
对于的递归算法如下:
void traverse(NodeType *h)
{
if(h!=null)
{
printf("%d",h->data);
traverse(h->next);
}
}
3 反向显示以h为首指针的单链表的所有节点值
设revtraverse(h)用于反向扫描链表h,其递归模型如下:

对于的递归算法如下:
void revtraverse(NodeType *h)
{
if(h!=null)
{
revtraverse(h->next);
printf("%d",h->data);
}
}
4 删除以h为首指针的单链表中值为x的第一个节点
设delnode(h,x)用于删除单链表h中第一个值为x的结点,其递归模型如下:

对于的递归算法如下:
void delnode(NodeType *&h,ElemType x){
NodeType *p;
if(h!=NULL) {
if(h->data == x){
p = h;
h = h->next;
free(p);
}
else
delnode(h->next,x);
}
}
5 删除以h为首指针的单链表中值为x的所有节点
设delall(h,x)用于删除单链表h中所有值为x的结点,其递归模型如下:
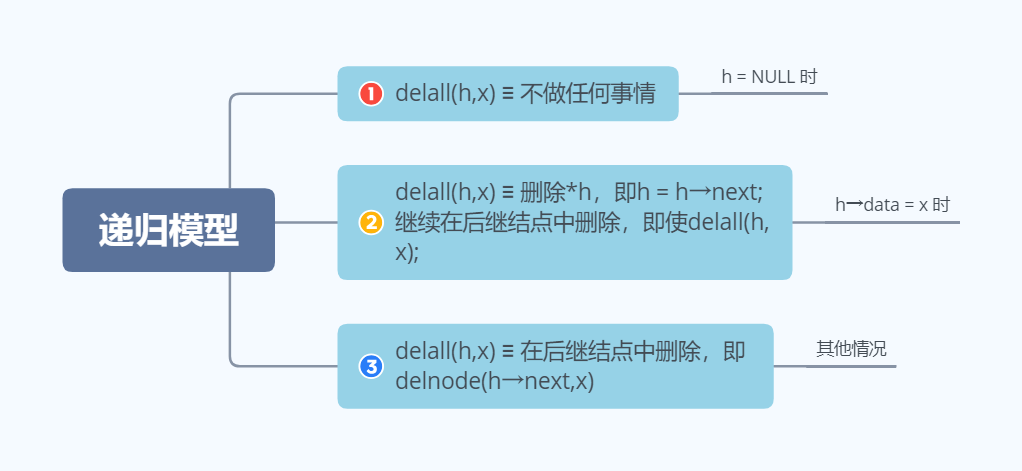
对于的递归算法如下:
void delall(NodeType *&h, ElemType x)
{
NodeType *p;
if(h!=NULL)
{
if(h->data == x) //若首结点的值为x
{
p = h;
h = h->next;
free(p);
delall(h,x); //在后继结点递归删除
}
else //若首结点值不为 x
delall(h->next,x); //在后继结点递归删除
}
}
6 输出以h为首指针的单链表中最大节点值
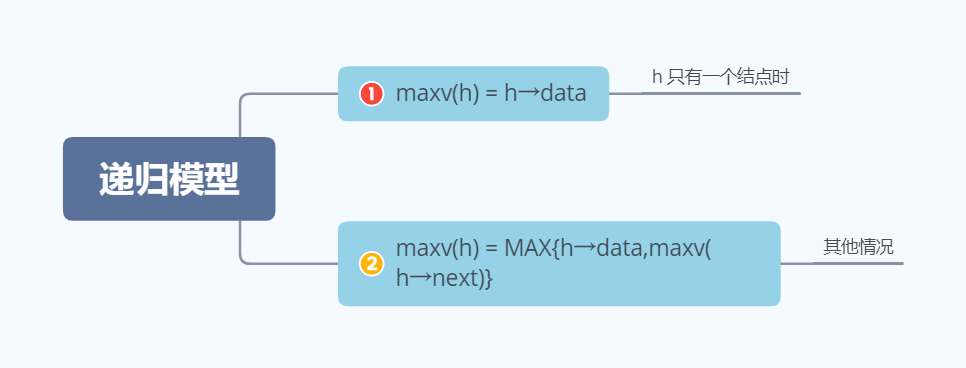
设maxv(h)用于计算单链表h的最大结点值,其递归模型如下(其中MAXV(x,y) 表示返回x和y的较大者):

对于的递归算法如下:
ElemType maxv(NodeType *h){
ElemType m;
if(h->next == NULL) //只有一个结点的情况
return (h->data);
m = maxv(h->next); //求后继结点的最大值
if(m>h->data)
return m;
else
return h->data;
}
7 输出以h为首指针的单链表中最小节点值
设minv(h)用于计算单链表h的最小结点值,其递归模型如下(其中MIN(x,y)表示返回x和y的较小者):

对于的递归算法如下:
ElemType minv(NodeType *h)
{
ElemType m;
if(h->next == NULL)
return h->data;
m = minv(h->next);
if(m>h->data)
return h->data;
else
return m;
}
8 删除并释放以h为首指针的单链表中所有节点
设release(h)的功能是删除并释放单链表h中所有结点,其递归模型如下:
对于的递归算法如下:
void release(NodeType *h)
{
if(h!=NULL)
{
release(h->next);
free(h);
}
}
参考
https://mp.weixin.qq.com/s/GiSqzg5827JyHrPQO0Z-hA
递归的定义
在定义一个过程或函数时出现调用本过程或本函数的成分,称之为递归。若调用自身,称之为直接递归。若过程或函数p调用过程或函数q,而q又调用p,称之为间接递归。
递归算法的设计
递归的求解过程均有这样的特征:先将整个问题划分为若干个子问题,通过分别求解子问题,最后获得整个问题的解。而这些子问题具有与原问题相同的求解方法,于是可以再将它们划分成若干个子问题,分别求解,如此反复进行,直到不能再划分成子问题,或已经可以求解为止。这种自上而下将问题分解、求解,再自上而下引用、合并,求出最后解答的过程称为递归求解过程,这是一种分而治之的算法设计方法。
简单递归算法设计方法:
例题
有一个不带表头节点的单链表,其节点类型如下:
typedef struct NodeType{ ElemType data; struct NodeType *next; }NodeType;
设计如下递归算法: 1 求以h为首指针的单链表的节点个数。 2 正向显示以h为首指针的单链表的所有节点值。 3 反向显示以h为首指针的单链表的所有节点值。 4 删除以h为首指针的单链表中值为x的第一个节点。 5 删除以h为首指针的单链表中值为x的所有节点。 6 输出以h为首指针的单链表中最大节点值。 7 输出以h为首指针的单链表中最小节点值。 8 删除并释放以h为首指针的单链表中所有节点。
解:设h为不带头节点的单链表(含n个节点),如图所示,h->next 也是一个不带头节点的单链表(含n-1个节点),两者除了相差一个节点外,其他都是相似的。
1 求以h为首指针的单链表的节点个数。
设count(h)用于计算单链表h的结点个数,其递归模型如下:
对于的递归算法如下:
int count(NodeType *h){ if(h==NULL) return 0; else return (1+count(h->next));}
2 正向显示以h为首指针的单链表的所有节点值。
设traverse(h)用于正向扫描单链表h,其递归模型如下:
对于的递归算法如下:
void traverse(NodeType *h){ if(h!=null) { printf("%d",h->data); traverse(h->next); }}
3 反向显示以h为首指针的单链表的所有节点值。
设revtraverse(h)用于反向扫描链表h,其递归模型如下:
对于的递归算法如下:
void revtraverse(NodeType *h){ if(h!=null) { revtraverse(h->next); printf("%d",h->data); }}
4 删除以h为首指针的单链表中值为x的第一个节点。
设delnode(h,x)用于删除单链表h中第一个值为x的结点,其递归模型如下:
对于的递归算法如下:
void delnode(NodeType *&h,ElemType x){ NodeType *p; if(h!=NULL) { if(h->data == x) { p = h; h = h->next; free(p); } else delnode(h->next,x); }}
5 删除以h为首指针的单链表中值为x的所有节点。
设delall(h,x)用于删除单链表h中所有值为x的结点,其递归模型如下:
对于的递归算法如下:
void delall(NodeType *&h, ElemType x){ NodeType *p; if(h!=NULL) { if(h->data == x) //若首结点的值为x { p = h; h = h->next; free(p); delall(h,x); //在后继结点递归删除 } else //若首结点值不为 x delall(h->next,x); //在后继结点递归删除 }}
6 输出以h为首指针的单链表中最大节点值。
设maxv(h)用于计算单链表h的最大结点值,其递归模型如下(其中MAXV(x,y) 表示返回x和y的较大者):
对于的递归算法如下:
ElemType maxv(NodeType *h){ ElemType m; if(h->next == NULL) //只有一个结点的情况 return (h->data); m = maxv(h->next); //求后继结点的最大值 if(m>h->data) return m; else return h->data;}
7 输出以h为首指针的单链表中最小节点值。
设minv(h)用于计算单链表h的最小结点值,其递归模型如下(其中MIN(x,y)表示返回x和y的较小者):
对于的递归算法如下:
ElemType minv(NodeType *h){ ElemType m; if(h->next == NULL) return h->data; m = minv(h->next); if(m>h->data) return h->data; else return m;}
8 删除并释放以h为首指针的单链表中所有节点。
设release(h)的功能是删除并释放单链表h中所有结点,其递归模型如下:
对于的递归算法如下:
void release(NodeType *h){ if(h!=NULL) { release(h->next); free(h); }}

 链表递归题型
链表递归题型


