A Parallel Particle Swarm Optimization Algorithm With Communication Strategies
A Parallel Particle Swarm Optimization Algorithm With Communication Strategies
Abstract
1 Introduction
粒子群优化(PSO)算法是基于进化计算技术(Eberhart&Kennedy 1995,Kennedy&Eberhart 1995)。粒子群算法是一种基于种群的进化算法,与一般进化算法有相似之处。然而,PSO的动机来自于对社会行为的模拟,这与遗传算法的自然选择方案不同(Goldberg 1989,Davis 1991,Gen&Cheng 1997)。这个比喻是指物体在空间中移动的多个集合(群),因此物体被认为具有位置和速度,并受到群中其他物体的影响。
PSO使用与遗传算法中的个体使用相对应的粒子群来处理搜索方案。每个粒子都等同于一个问题的候选解。粒子将根据调整后的速度移动,该速度基于相应的粒子经验和其同伴的经验。对于D维函数f(.),第i个粒子用于第Th次迭代可以表示为XTI=(XTI(1),XTI(2),.。。。,xti(D))。
2 Parallel Particle Swarm Optimization
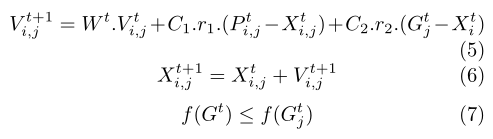
其中 i = 0, . . . Nj - 1, j = 0, . . . S − 1, S (= 2m) 为组数(m 为正整数),Nj 为第 j 组的粒子大小,Xti,j 为第 t 次迭代时第 j 组中的第 i 个粒子位置,是第 j 组第 i 个粒子在第 t 次迭代时的速度,Gtj 是第 j 组所有粒子中从第一次迭代到第 t 次迭代的最佳位置,Gt 是从第 j 组所有粒子中的最佳位置第一次迭代到第 t 次迭代。
如上所述,我们为并行粒子群优化算法开发了三种通信策略。图1所示的第一种通信策略是基于这样的观察设计的,即如果参数是独立的或只是松散相关的,那么较好的粒子可能很快就会得到好的结果。因此,每组GT中最好的粒子的多个副本被突变,并且这些突变的粒子在每R1次迭代中迁移并替换其他组中最差的粒子。
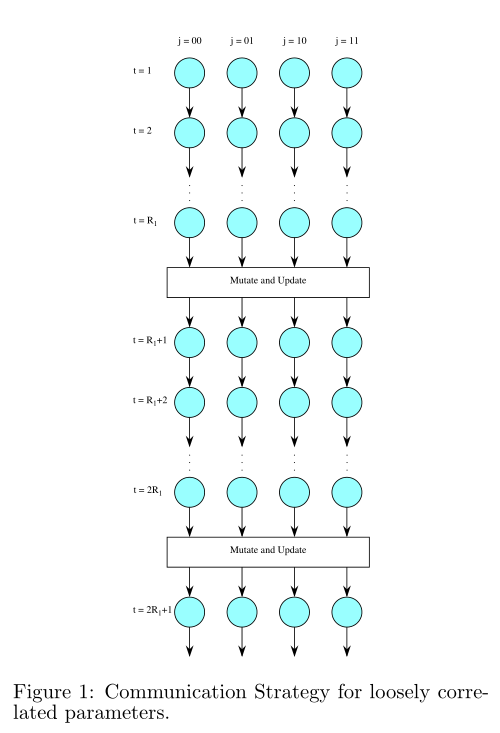
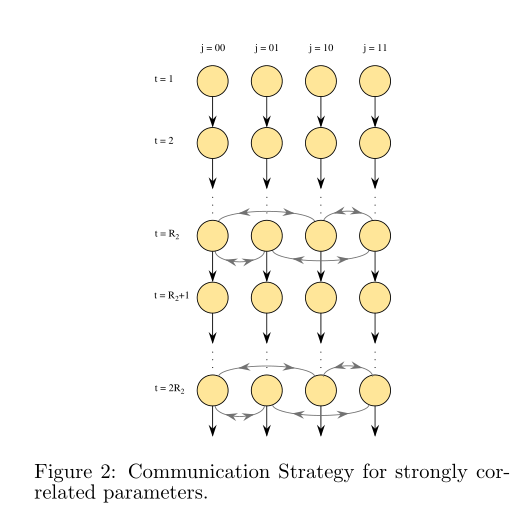

完整的并行粒子群优化(PPSO)算法及其三种通信策略如下:
1.初始化:为第j组生成nj个粒子xti,j,i=0,.。。。Nj−1,j=0,.。。。S−1,S是组数,nj是第j组的粒子大小,t是迭代次数。
设置t=1。
2.评价:对每组中每个颗粒的f(xti,j)值进行评价。
3. 更新:使用等式(5)、(6)和(7)更新速度和粒子位置。
4.沟通:三种可能的沟通策略如下:
策略 1:将所有粒子 Gt 中最好的粒子迁移到每个组,并变异 Gt 以替换每个组中的较差粒子,并在每 R1 次迭代中为每个组更新 Gtj 与 Gt。
策略2:将第j个组的最佳粒子位置Gtj迁移到第q个组,以每R2次迭代替换每个接收组中一些较差的粒子。这里q=j⊕2m,j=0,。。。S−1,m=0,.。。。N−1,S=2n。
策略3:将小组分成两个小组。在每个R1迭代中将通信策略1应用于子组1,在每个R2迭代中将通信策略2应用于子组1和子组2。
5. 终止:重复步骤 2 到步骤 5,直到达到函数的预定义值或迭代次数。记录函数 f(Gt) 的最佳值和所有粒子 Gt 中的最佳粒子位置。
3 Experiments
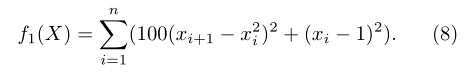
第二个函数是广义 Rastrigrin 函数,可以表示为:
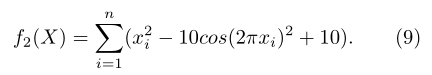
第三个函数是广义 Griewank 函数,如下所示:
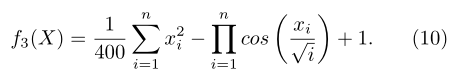
第一个实验是为了测试第一种PPSO通信策略的性能,该策略适用于解的参数松散相关的情况,例如对于Rastrigrin和Rosenbrock函数。第二个实验测试了第二种策略的性能,当解的参数相关性更强时,就像Griewank函数的情况一样。最后的实验测试了第三种通信策略对所有三种功能的性能。所有这三个实验都与PSO在50次运行中线性减小的惯性权重进行了比较(Shih&Eberhart,1999)。
PSO和PPSO的函数参数如表1所示,我们不限制X、C1和C2的值设置为2,最大迭代次数为2000次,W0t=0.9,W2000t=0.4,维数设置为30。

为了公平比较,组的数量×每组的粒子数保持不变-PSO的粒子大小为160,PPSO的粒子大小分别为8×20、4×40和2×80。对于第一个实验,将通信迭代次数设置为20次,并对最佳粒子位置进行迁移和变异,以25%、50%、75%和100%的速率替换接收组的粒子。如表2和表3所示,第一种通信策略对独立或松散相关的解决方案参数有效。
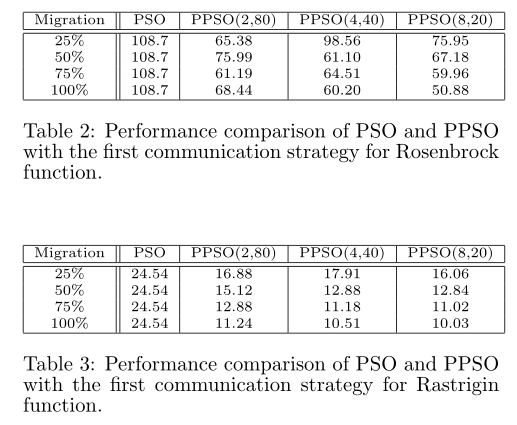
对于第二个实验,通信的迭代次数设置为100,每个接收组替换的较差粒子数设置为1和2。实验结果如表4所示,8组的第二个通信策略可能会提高性能提升高达 66%。

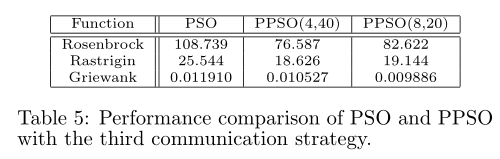
对于第三个实验,参数与第一个和第二个实验相同。 50%的粒子在接收组中被替换为第一种通信策略,2个粒子在接收组中被替换为第二种通信策略。如表 5 所示,混合通信策略对所有三个功能都有效。

 一种具有通信策略的并行粒子群优化算法
一种具有通信策略的并行粒子群优化算法


