A Compact Adaptive Particle Swarm Optimization Algorithm in the Application of the Mobile Sensor Localization

A Compact Adaptive Particle Swarm Optimization Algorithm in the Application of the Mobile Sensor Localization

一种紧凑型自适应粒子群优化算法在移动传感器定位中的应用

文章信息

博客内容仅用于学习。

Wei-Min Zheng , Ning Liu , Qing-Wei Chai , and Shu-Chuan Chu

College of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China

Correspondence should be addressed to Shu-Chuan Chu; scchu0803@gmail.com

Received 12 September 2021; Accepted 20 October 2021; Published 9 November 2021


Academic Editor: Chi-Hua Chen

Copyright © 2021 Wei-Min Zheng et al. This is an open access article distributed under the Creative Commons Attribution
License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is
properly cited.

0. Abstract

　　移动传感器网络可以实时感知和采集监控区域内被监控对象的数据信息。然而，只有当知道节点的位置时，收集的信息才有意义。本文主要对移动传感器定位技术中的蒙特卡罗定位(MCL)算法进行优化。近年来，启发式算法的快速发展为许多复杂问题提供了解决方案。将紧凑策略与自适应粒子群算法相结合，提出了一种紧凑自适应粒子群算法(CAPSO)。紧凑策略将每个粒子的具体位置替换为粒子群的分布概率，大大减少了内存占用。在CEC2013的28个测试函数上测试了CAPSO的性能，并与现有的一些启发式算法进行了比较，证明了CAPSO具有更好的性能。同时，将CAPSO算法应用到MCL技术中，提高了节点定位的精度，并与其他启发式算法在MCL定位精度上进行了比较，结果表明CAPSO算法具有更好的性能。

1. Introduction

　　元启发式算法是受自然界各种生物生活习性启发的算法。元启发式算法可以有效地解决生活中的许多问题[1]，广泛应用于金融、交通、物理、化学、军事等领域[2-8]。没有免费午餐定理[9，10]证明了任何优化算法不可能适用于所有情况。因此，各种元启发式算法及其改进算法不断被提出以解决更复杂的问题[11-13]。

　　粒子群优化 (PSO) 是 Kennedy 和 Eberhart [14, 15] 提出的最重要的元启发式算法之一。他们观察并分析了鸟类的觅食行为，然后提出了这个算法。粒子群优化算法中存在全局最优位置和个体最优位置。这两个位置在每次迭代中根据适应度值进行更新，使算法更接近问题的最优解。粒子群算法的参数少、结构简单、搜索速度快等特点使其适用于众多领域。还有很多改进的 PSO 算法，如受限粒子群优化（CPSO）[16]、完全知情粒子群优化（FIPSO）[17]、综合学习粒子群优化（CLPSO）[18]、智能单粒子优化（ ISPO) [19] 和自适应粒子群优化 (APSO) [20]。 PSO 可以解决许多问题，例如优化神经网络 [21]、解决车辆路径问题 [22、23]、调度工作流调度 [24] 以及定位无线传感器节点 [25]。 APSO算法在原有PSO算法的基础上，引入进化状态评价策略、精英学习策略、系统自适应参数策略，对原有PSO算法进行改进。 APSO解决了原有PSO算法收敛速度慢、容易陷入局部最优的问题。本文主要尝试将紧凑策略与APSO相结合，提高移动传感器定位的准确性。

　　移动传感器网络的应用是当节点的位置信息已知时为人们提供服务[26]。没有位置信息的节点测量的数据在许多情况下是没有意义的[27]，例如森林火灾检测[28]。因此，为了充分利用监视数据，需要知道节点[29，30]的位置信息。为每个节点安装GPS是解决这一问题的最佳方式，但这种方式昂贵且耗能。因此，应随机选择少量节点安装GPS，然后通过GPS节点的定位，利用定位技术获得其他节点的位置[31]。移动传感器和固定无线传感器之间最显著的区别在于它的移动性[32，33]。这种移动性使得传感器能够更好地收集指定区域内的有效信息，解决了由于特定位置节点的损坏而无法收集特定区域内信息的问题。移动传感器的部署更加方便，不需要像固定无线传感器部署节点那样的详细设计[34]。

　　紧凑的思想是用粒子群的行为概率来代替每个个体的位置和速度来表示粒子群。该紧凑算法可以有效地节省存储空间[20]，在小型机器人[35]、远程办公室[36]、航天飞机控制[37]中都有应用。使用紧凑思想的算法也不断被提出，如紧凑人工蜂群(CABC)[38]、紧凑正弦余弦算法(CSCA)[39]、紧凑BAT算法(CBA)[40]和紧凑粒子群优化(CPSO)[41]。然而，将紧凑算法与APSO算法相结合的问题却未被提及。本文希望将COMPACT算法的思想与APSO算法相结合，提出一种内存小、收敛速度快的CAPSO算法，并将其应用于移动传感器定位。

　　本文的其余部分安排如下。第二部分介绍了相关工作的基础，简要介绍了APSO算法和移动传感器定位技术。第三部分介绍了算法的改进方法和步骤。第四节测试算法的性能，并与同类算法进行比较。第五部分将改进算法应用于移动传感器定位。第六部分给出了本文的结论。

2. Related Work

　　本节将简要介绍APSO和移动传感器定位技术MCL。

2.1. Particle Swarm Optimization

(基础知识不再赘述)

2.2. Adaptive Particle Swarm Optimization

APSO具体机制见：

https://www.cnblogs.com/3cH0-Nu1L/p/15569411.html

2.3. Mobile Sensor Localization

　　本节主要介绍MCL移动节点定位方法[42，43]。移动传感器网络中的移动节点以随机速度和随机方向移动。移动节点相对于固定节点的最大优势在于其移动性。移动节点解决了由于特定位置的节点损坏而无法收集某一区域的信息的问题。MCL方法主要分为三个阶段：初始化阶段、预测阶段和过滤阶段[44]。在初始化阶段，为每个节点指定移动区域和最大移动速度。在预测阶段，对移动节点的位置进行初步估计。节点移动的速度和方向是不确定的。运动后的位置在一个圆圈内。这个圆的中心是最后一个节点的位置，半径是速度和定位间隔时间的乘积，如图2所示:

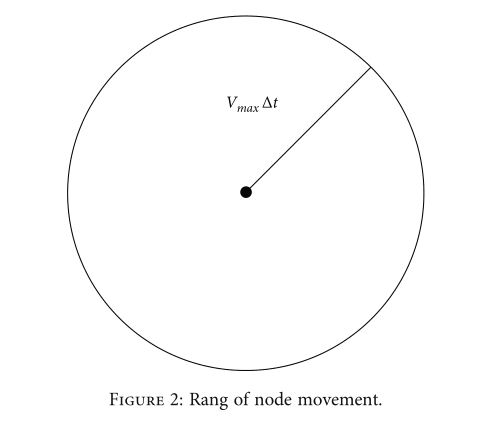
　　过滤阶段是MCL最关键的阶段。
　　首先，MCL根据锚节点与未知节点的距离，确定哪些锚节点是未知节点的一跳信标节点，哪些锚节点是未知节点的两跳信标节点。

　　然后，MCL获得一跳信标节点集B1和两跳信标节点集B2。

　　其次，在可能的区域中随机选择点，并根据选择的点是否在一跳和两跳信标节点的范围内对不一致点进行过滤。
过滤条件如公式(8)所示：

 

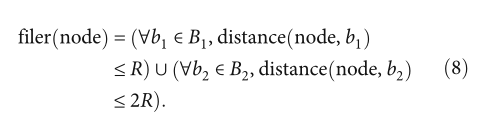
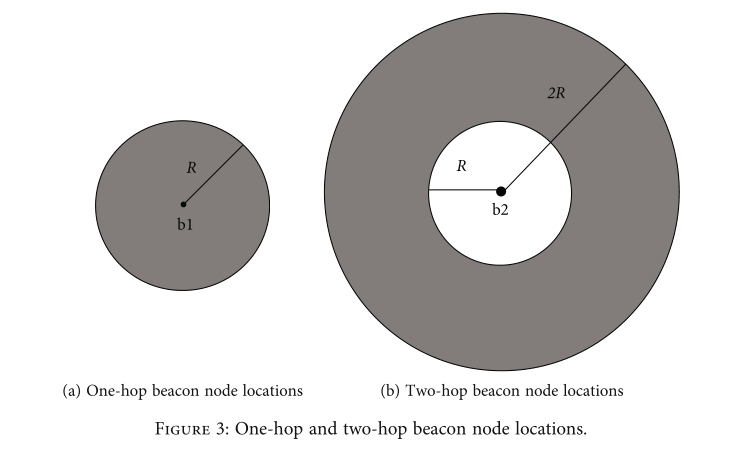
　　图 3 中的灰色区域是满足过滤条件的点集。 MCL根据未知节点到锚节点的跳数在一个小空间内定位未知节点的位置。等式（8）过滤掉落在这个小空间中的点。为了防止偶然性，将这个小空间中所有点的坐标平均为MCL最初预测的未知节点的位置。最后，通过式（9）估计过滤后的合格点以估计未知节点的位置，其中N表示满足过滤条件的点的总数，node表示满足过滤条件的节点的位置。

 

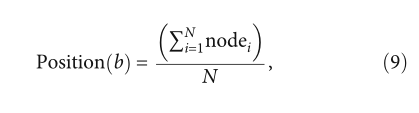
3. Compact Adaptive Particle Swarm Optimization

　　本节主要介绍紧凑策略的思想以及如何将紧凑策略应用于自适应粒子群优化算法。

3.1. Compact Strategy

　　紧凑策略的主要目的是在不改变原算法性能甚至提高原算法性能的情况下减少内存使用。如果减少内存使用，运行速度自然会提高。紧凑策略使用 PV 扰动向量来表示种群的整体运动状态，而不是简单地使用每个个体的位置和速度来表示种群状态。扰动向量 PV 定义为 PVg = ðμg, σgÞ，其中 μ 表示扰动向量的平均值，σ 表示扰动向量的标准差，g 表示当前迭代更新次数。

　　紧凑策略最终返回 (0,1) 之间的值。 PV向量由μ和σ组成，通过μ和σ可以计算概率分布函数（PDF）。然后，可以通过PDF计算累积分布函数（CDF）。 PDF 和 CDF 的计算公式见式（10）和（11）。

 

 

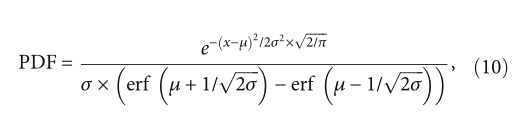
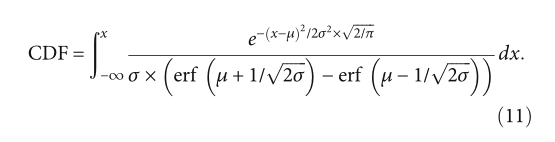
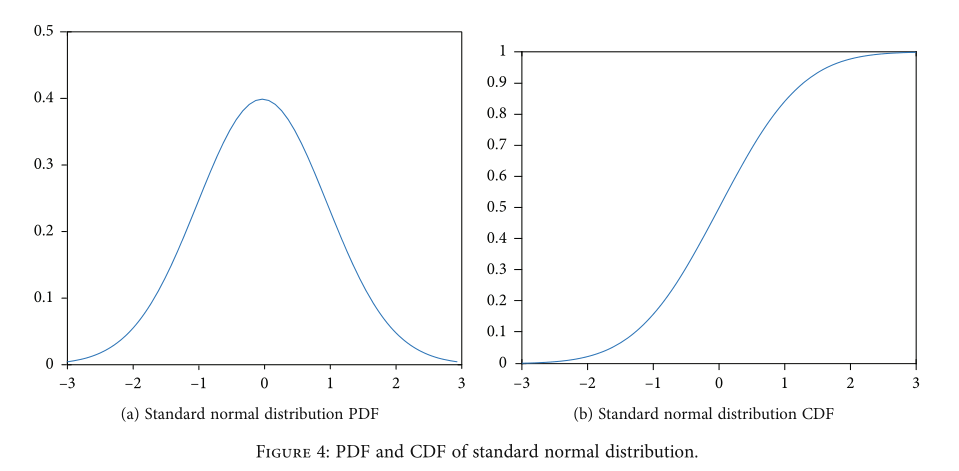
 　　累积分布函数的CDF取值范围为(0,1)，也是compact策略返回的取值范围。以标准正态分布为例，标准正态分布的PDF和CDF如图4所示。

 

　　compact 策略的另一个重要内容是 PV 扰动向量的迭代更新。紧凑型策略以比较为基础，通过竞争博弈机制获得胜负。然后，通过更新迭代策略对其进行更新。更新公式如公式（12）和（13）所示。

其中g表示当前迭代时间，Np表示虚拟种群的数量。PV扰动向量的平均值μ一般设置为0，PV扰动向量的标准差σ一般设置为10，以避免初始化时局部最优的偶然性。通过大量实验证明，当虚拟种群数量设置为300时，效果最好。因此，np通常设置为300。

 

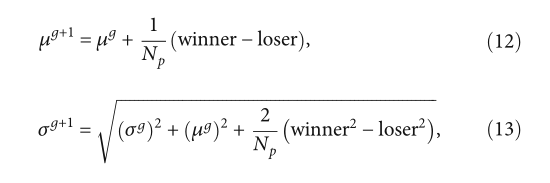
3.2. Implementation of the Compact Strategy in APSO

　　紧凑策略基于比较。换句话说，必须有一个大小为 2 的博弈机制，这样才能产生赢家和输家，然后才能更新 PV 扰动向量中的 μ 和 σ。 APSO可以通过适应度值的比较来满足这个条件，所以APSO满足了compact策略的首要条件，compact策略可以与APSO结合，达到减少内存、提高运算速度的目的。例如，如果粒子群中有 30 个粒子，解决问题的维度也是 30 维，那么 APSO 需要 900 个存储单元来存储每个粒子在每个维度中的位置信息。而cAPSO只需要60个存储单元就可以使用PV扰动向量在每个维度存储粒子群，显着节省了存储空间。存储空间的节省减少了对内存的读写次数，算法的速度也会相应提高。

　　cAPSO通过整体概率分布来表达粒子群的位置，compact策略的取值范围在(0,1)之间，假设y为compact策略的返回值。那么，紧凑策略的返回值应该与实际的持仓范围通过公式（14）对应起来。

 

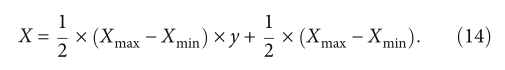
　　原始APSO中的演化因子f由公式(3)和(4)计算。但是，由于用分布概率来表示粒子群在CAPSO中的位置，所以用公式(15)代替了演化因子f的计算。

 

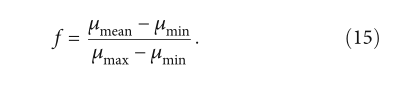
　　cAPSO将PV扰动向量生成的本次迭代位置的适应度值与当前个体最优位置的适应度值进行比较，生成赢家和输家。生成的赢家和输家使用方程（12）和（13）更新扰动向量PV，然后在下一次迭代中生成粒子群的位置概率分布。

4. The Performance Test of cAPSO

　　本节主要在 CEC2013 [45] 的 28 个测试函数中测试 cAPSO 算法。本文将 cAPSO 与常见的启发式算法和常见的紧凑算法进行了比较。 CEC2013 中的 28 个测试函数包括 8 个混合函数、15 个多峰函数和 5 个单峰函数。这28个功能很有代表性。 28 个功能由 f1 到 f28 表示。每个实验在比较过程中保持常用参数一致，以保证比较的公平性。

4.1. Performance Comparison of cAPSO and Common Heuristic Algorithms

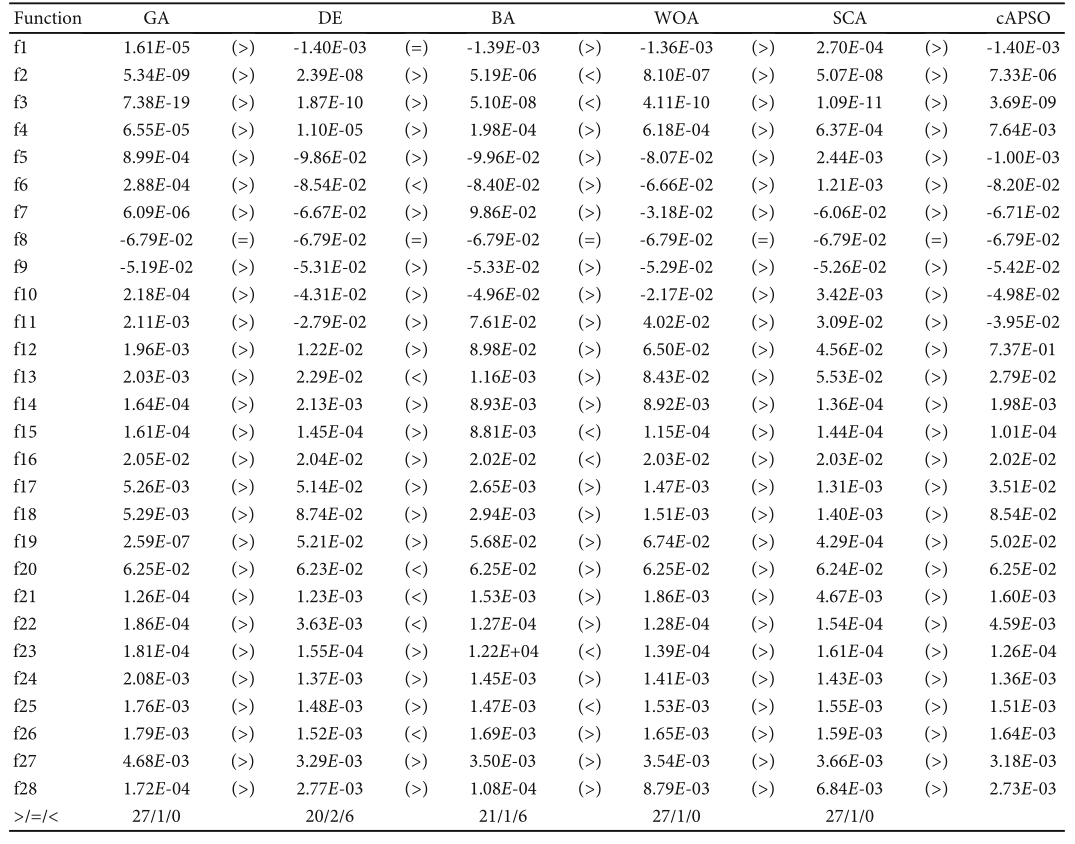
　　在本节中，将 cAPSO 与遗传算法 (GA) [46]、差分进化算法 (DE) [47]、鲸鱼优化算法 (WOA) [48]、蝙蝠算法 (BA) [49] 和正余弦算法进行了比较在 CEC2013 的 28 个测试函数上的算法（SCA）[50]。同时，在 Wilcoxon 符号秩检验下，每个算法与 cAPSO 算法相比的整体性能在显着水平 α = 0:05 下测量。对每个测试函数进行20次测试，然后取平均值以避免偶然发生。为保证算法在测试时的公平性，设置问题的维度为50，种群数量设置为60，迭代次数设置为3000，CEC2013中的搜索范围要求为[-100,100 ]。表 2 显示了 cAPSO 和常见启发式算法的性能比较。此外，表 2 还表明，每种算法都是在 Wilcoxon 符号秩检验下测量的，显着性水平为 α = 0:05。符号“>”表示cAPSO的性能优于其他启发式算法，符号“=”表示cAPSO的性能与其他启发式算法相同，符号“<”表示cAPSO 的性能比其他启发式算法差。表 2 的最后一行总结了所有测试功能的比较结果。

　　表2显示，与DE相比，CAPSO的测试性能在20个函数上优于DE，在2个函数上与DE相同，在6个函数上逊于DE。与BA相比，CAPSO在21个功能上优于BA，在1个功能上与BA相同，在6个功能上逊于BA。与GA、WOA和SCA算法相比，Capso算法在函数f8上的性能与GA、WOA和SCA算法相当，但在其他函数上优于其他算法。可以看出，与紧凑策略相结合的Capso算法比普通启发式算法的性能有了很大的提高。

　　为了进一步描述算法的效果，本文采用收敛曲线进行评价。由于许多算法的收敛性非常相似，在收敛曲线上表现不明显，因此本文选取了几条分散的代表性曲线进行展示。图5显示了算法在一些测试函数上的收敛过程。横轴代表迭代次数，垂直轴代表不同算法的适应值。适应值越小，该测试函数的性能越好。从图5可以看出，所提出的Capso算法在f4、f9、f11、f17和f27上的性能优于其他启发式算法。但测试函数在F13和F22上的性能比DE差，在F17上的性能不如BA。

表 2：cAPSO 与常见启发式算法的性能比较以及每个算法在显着性水平 α = 0:05 的 Wilcoxon 符号秩检验。

4.2. Performance Comparison of cAPSO and Common Compact Algorithms

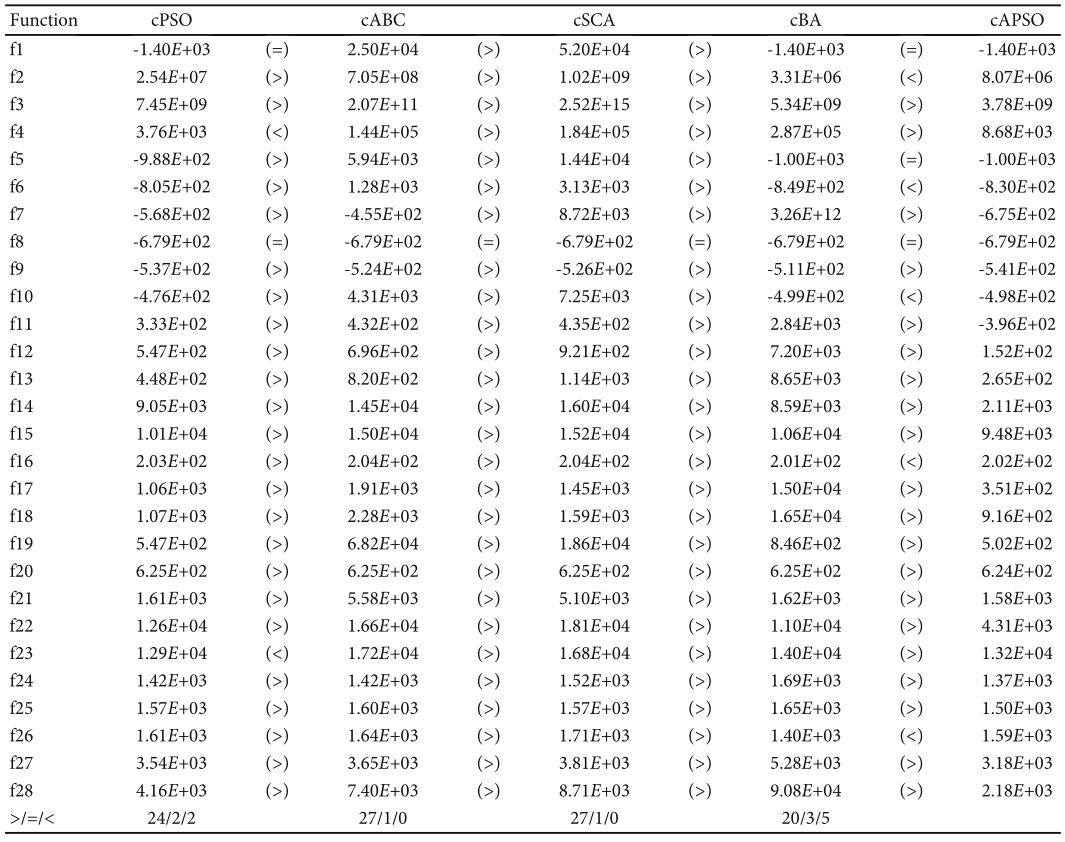
　　在本节中，cAPSO 在 CEC2013 的 28 个测试函数上与 cPSO [41]、cABC [38]、cSCA [39] 和 cBA [40] 进行了比较。同时，在 Wilcoxon 符号秩检验下，每个算法与 cAPSO 算法相比的整体性能在显着水平 α = 0:05 下测量。对每个测试函数进行20次测试，然后取平均值以避免偶然发生。为了保证算法在测试时的公平性，设置问题的维度为50，种群数量设置为60，迭代次数设置为3000，虚拟种群数量设置为300， CEC2013 中的搜索范围要求为 [-100,100]。表 3 显示了 cAPSO 和常见紧凑算法的性能比较。此外，表 3 还显示每个算法都是在 Wilcoxon 符号秩检验下测量的，显着性水平为 α = 0:05。符号“>”、“=”和“<”与第 4.1 节中的含义相同。表 3 的最后一行总结了所有测试功能的比较结果。

　　表 3 显示，与 cPSO 相比，cAPSO 的测试性能在 24 个函数上优于 cPSO，在 2 个函数上与 cPSO 相同，在 2 个函数上比 cPSO 差。与cBA相比，cAPSO的测试性能在20个功能上优于cBA，在3个功能上与cBA相同，在5个功能上比cBA差。与 cABC 和 cSCA 相比，cAPSO 在函数 f8 中的性能与这两种算法相同，但在其他函数中优于这两种算法。可以看出，cAPSO在紧凑算法方面具有很强的竞争力，在性能上也比其他紧凑算法有优势。

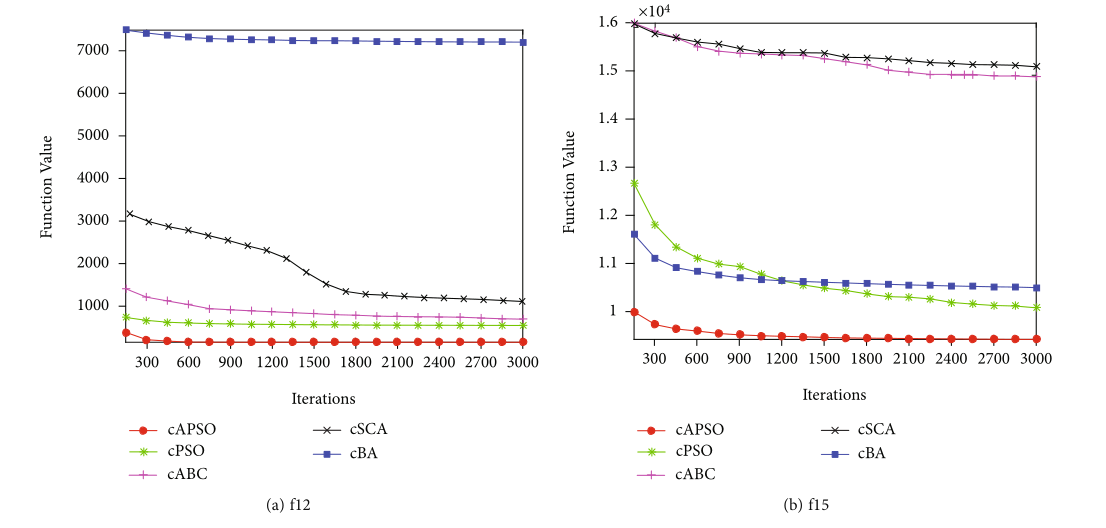
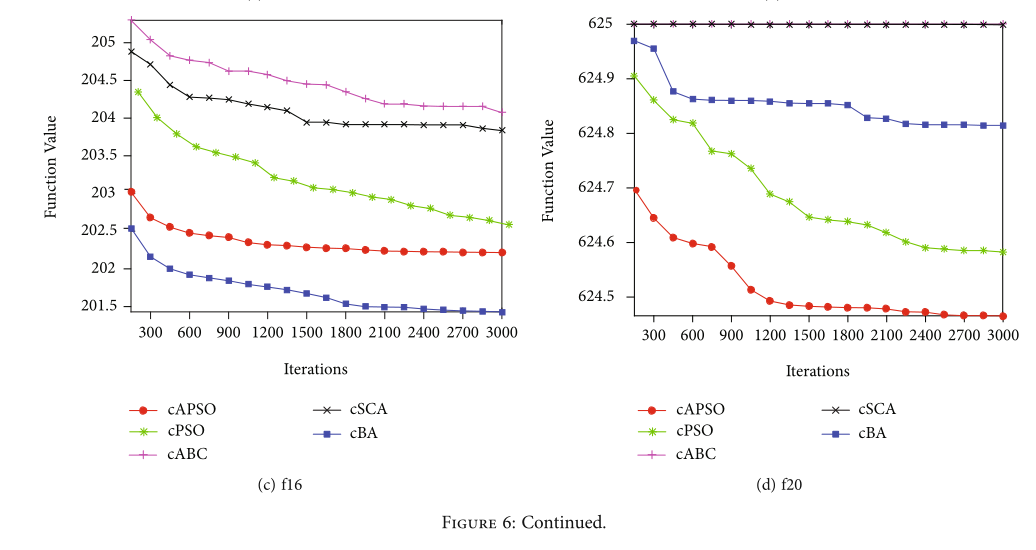
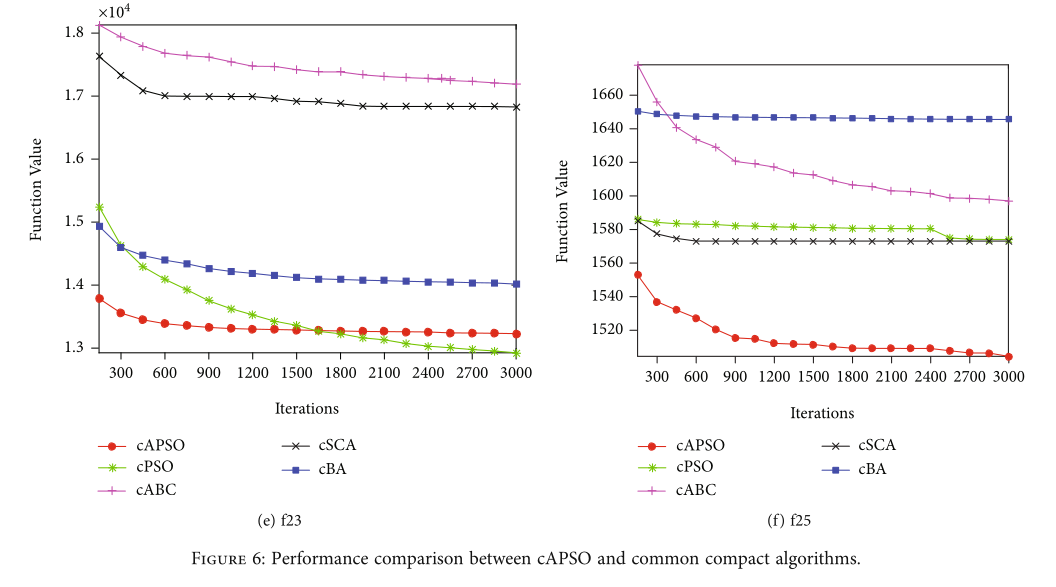
　　与第 4.1 节一样，图 6 显示了所提出的 cAPSO 和其他紧凑算法的代表性收敛曲线。从图 6 可以看出，所提出的 cAPSO 算法在 f12、f15、f20 和 f25 上的性能优于其他紧凑型算法。但是测试函数在f16上的表现不如cBA，在f23上的表现比cPSO差。

表 3：cAPSO 与常见紧凑算法之间的性能比较以及每个算法在显着性水平 α = 0:05 的 Wilcoxon 符号秩检验。

 

 

5. Application of cAPSO in Mobile Sensor Localization

　　本部分主要将Capso应用于移动传感器定位技术MCL，并与原有的MCL、基于WOA的MCL和基于BA的MCL在不同锚节点数量和不同通信半径下进行了比较。通过MCL技术直接找出误差小的位置，需要大量的时间和计算能力。首先通过MCL技术获得误差较大的位置，然后在获得的位置周围应用CAPSO进行进一步优化。Capso广播其周围的节点，广播节点根据Capso的想法移动。将移动后的位置与历史最优位置进行比较，以更新最优位置。经过一定次数的迭代，得到最优位置作为MCL定位技术的最终位置。移动传感器定位技术是一种利用锚节点信息来估计未知节点位置的技术，因此位置误差成为该技术的关键。位置误差越小，越有利于信息的准确性。将启发式算法应用于MCL技术，可以更好地定位未知节点，减少定位误差。更精确的位置坐标由误差函数迭代更新。误差函数定义为公式(16)。

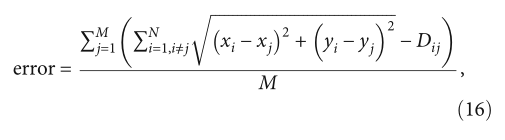
5.1. Influence Analysis of Different Anchor Nodes

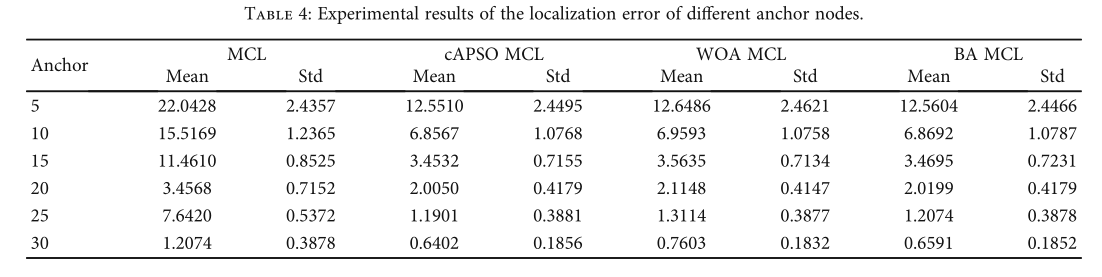
　　在模拟实验中，200个节点随机分布在200m×200m的范围内，锚节点的数量分别为5、10、15、20、25、30、35和40，因此未知节点的数量为195、190、185、180、175、170、165和160。将通信半径设置为50m，在相同参数下进行了20次仿真实验，并计算其平均值作为误差结果。分别应用Capso、WOA和BA算法进行仿真实验。实验结果如表4所示。

　　由表 4 可知，当节点总数为 200，通信半径为 50 m 时，锚节点数越多，未知节点的位置越准确，误差值越小。表 4 清楚地表明，启发式算法优化后的定位误差远小于原始 MCL。在组合不同的启发式算法中，可以清楚地看到，虽然cAPSO算法每次在标准差上并不优于其他算法，但在误差均值上却比其他启发式算法有更好的结果。

5.2. Influence Analysis of Different Communication Radius

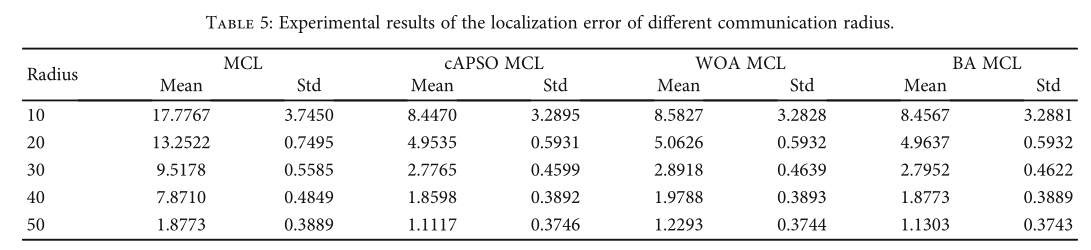
　　仿真实验在200m×200m的范围内随机分布200个节点，锚节点数量设置为30个，通信半径分别设置为10m、20m、30m、40m和50m，在相同参数下进行了20次仿真实验，并计算其平均值作为误差结果。分别应用Capso、WOA和BA算法进行仿真实验。实验结果如表5所示。

　　由表 5 可知，当节点总数为 200，锚节点数为 30 时，通信半径越大，未知节点的位置越准确，误差值越小。表 5 清楚地表明，启发式算法优化后的定位误差远小于原始 MCL。在组合不同的启发式算法中，也可以清楚地看出cAPSO算法在误差均值的比较上优于其他启发式算法。

 

6. Conclusion

　　本文提出了一种结合紧凑策略的改进APSO算法，并将其应用于移动传感器定位。紧凑策略不再存储每个粒子在每个维度上的位置，而是通过概率模型的运算来描述每个维度上粒子的分布特征。紧凑策略可以很好地减少内存的使用。本文测试了CAPSO在CEC2013的28个测试函数上的性能，并与常用的启发式算法GA、DE、BA、WOA和SCA以及常用的紧凑策略启发式算法CPSO、CABC、CSCA和CBA进行了比较。比较结果表明，CAPSO具有更好的测试性能。最后将CAPSO应用于移动传感器定位技术MCL，并与基于WOA的MCL和基于BA的MCL进行了比较。结果表明，基于CAPSO的MCL更有效地解决了这一问题。