A Node Location Method in Wireless Sensor Networks Based on a Hybrid Optimization Algorithm
A Node Location Method in Wireless Sensor Networks Based on a Hybrid Optimization Algorithm
基于混合优化算法的无线传感器网络节点定位方法
文章信息
博客内容仅用于学习。
Jeng-Shyang Pan ,1,2 Fang Fan,1,3 Shu-Chuan Chu ,1 Zhigang Du,1 and Huiqi Zhao3
1College of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao, 266590 Shandong, China
2Department of Information Management, Chaoyang University of Technology, Taichung, Taiwan
3College of Intelligent Equipment, Shandong University of Science and Technology, Taian, 271019 Shandong, China
Correspondence should be addressed to Shu-Chuan Chu; scchu0803@gmail.com
Received 14 July 2020; Revised 20 August 2020; Accepted 6 September 2020; Published 6 October 2020
Academic Editor: Chao-Yang Lee
Copyright © 2020 Jeng-Shyang Pan et al. This is an open access article distributed under the Creative Commons Attribution
License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is
properly cited.
0. Abstract
无线传感器网络(WSN)已逐渐融入物联网(IoT)的概念,成为物联网的关键技术之一。本文研究了人工智能领域的优化算法,有效地解决了无线传感器网络中的节点定位问题。具体地说,我们提出了一种基于鲸鱼优化(WOA)和准仿射变换进化算法(QUATRE)的混合算法WOA-QT。它巧妙地结合了两种算法的优点,既保留了WOA独特的框架优势,又具有Quatre优秀的协同进化能力。为了进一步节省优化时间,该算法引入了动态缩小搜索空间的辅助策略。为了保证评价的公正性,本文选取了30种不同类型的基准函数,从多个角度进行了实验。实验结果表明,WOA-QT的优化质量和效率非常显著。利用该算法对基于接收信号强度指示(RSSI)的加权质心定位(WCL)算法进行了优化,获得了满意的定位精度。这体现了该算法在实际应用中的较高价值。
1. Introduction
随着物联网(IoT)的发展到今天,可以说已经完成了最初设想的基本任务,即人、机、物的互联[1]。然而,人们不再满足于简单的组网,提出了更高的要求。随着规模的迅速扩大,物联网产生了数量惊人的实时监控数据[2]。毫无疑问,对这些数据的科学管理需要“超级大脑”,智能化成为进化升级的必然选择。人工智能 (AI) 完全胜任此角色。人工智能的历史比物联网的历史要长得多,但一直受到技术开发难度大、成果转化动能不足的困扰。近年来,人工智能在技术层面取得突破性进展,让人对它的未来充满信心和希望。如何将人工智能从实验室引导到各种实际应用场景中,是一项具有挑战性的任务。蓬勃发展的物联网为人工智能充分发挥潜能提供了广阔舞台,自然存在的数据源不断为其提供动力。依托物联网构建的成熟平台,人工智能可以满足最迫切的技术落地需求。虽然物联网在产业链和规模上已经具备了相当的体量,但很多关键技术仍需打磨和完善。长期以来,物联网一直在思考寻求长足进步和可持续发展,而人工智能的赋能恰恰为其发展打开了重要的机遇之窗。因此,AIoT(Artificial Intelligence of Things)一词应运而生,可以理解为人工智能与物联网的融合。
人工智能涵盖了广泛的技术,其中的优化算法受到了研究人员的广泛关注。在众多优化算法中,元启发式算法最为活跃。其中一些算法的灵感来自于自然界中的进化现象,以遗传算法(GA)[3]和差分进化算法(DE)[4]为代表。一些算法受到生物群体行为的启发,包括粒子群优化算法(PSO)[5]、人工蜂群算法(ABC)[6,7]、猫群优化算法(CSO)[8,9]、WOA[10,11]和共生生物搜索算法[12,13]。有些与物理或数学规则有关,如黑洞(BH)[14,15]和夸特[16,17]。不幸的是,没有一个算法能够根据NFL定理[18]解决所有优化问题。这激发了研究人员无尽的热情,要么提出新的算法和技术,要么改进现有的[19,20],或者结合不同的算法[21]。结果表明,该算法的混合策略在很多情况下是值得尝试的。本文混合了WOA和QUATRE两种算法,并介绍了动态缩小搜索空间的技术。在基准函数的测试中,发现混合算法取得了很大的进步。
作为物联网的关键核心技术,无线传感器网络已经从最初的军事应用扩展到环境生态保护、医疗健康监测、农业种植、交通管理、物流管理等大量民用领域[22]。无线传感器网络的主要研究内容包括网络拓扑控制和网络协议、节点部署[23、24]、网络安全[25、26]、定位技术、数据融合和数据管理。无线传感器网络的发展也面临着诸多挑战。例如,如何利用有限的通信能力来完成传感数据的传输需要进一步的研究。而如何通过低功耗设计最大化网络的使用寿命也是亟待解决的问题。本文将优化算法引入到无线传感器网络节点定位问题中,取得了令人满意的定位精度。
本文其余内容如下:第二部分是相关研究工作,主要是对WOA和QUATRE的简单介绍;第三部分详细讨论了两种算法的组合和改进策略;第四部分是基于基准函数的实验数据统计与分析;第五部分是利用算法实现WSN中的定位;最后一部分是总结和展望。
2. Related Works
2.1. Whale Optimization Algorithm (WOA)
作为一种基于群体智能的元启发式优化算法,WOA设计精巧,富有特色。它模拟座头鲸群体的捕猎行为。受这种狩猎方式的启发,WOA设计了三种模式:搜索猎物、包围猎物和气泡网攻击。首先,初始化每个鲸鱼的位置:x!=§x1,x2,⋯,xn?,代表n维候选解。通过勘探开发两个阶段的配合,逐步找到最优位置(即最优解)。
算法中出现了三个向量:A!,C!和D!。A!还有C!定义如下:
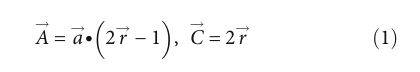
(1)探索:搜索模式
WOA 的探索阶段模拟了鲸鱼在海洋中寻找猎物的过程。使用随机选择的搜索代理来更新解决方案。为了达到全局搜索的目的,搜索代理被迫离开参考鲸鱼。探索的位置更新公式如下:
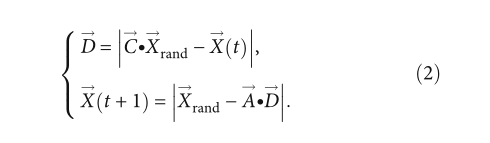
(2) Exploitation
WOA的发展阶段包括两种模式:包围模式和气泡网攻击模式。
2.1.1. Encircling Mode
座头鲸一旦找到猎物,就会包围它们。由于最佳位置未知,因此假设当前最佳解是目的地或近似最佳位置。其他搜索代理将参考当前最优来更新其位置,如公式(3)所示:
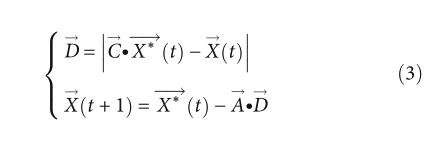
2.1.2. Bubble-Net Attacking Mode
气泡网攻击是座头鲸最有特色的捕猎方式。除了在猎物周围游动外,鲸鱼还沿着螺旋形的路径移动。WOA会创建一个螺旋方程来模拟整个距离,如以下公式所示:

2.2. QUasi-Affine Transformation Evolutionary (QUATRE) Algorithm
Quatre是一种基于拟仿射变换的协同进化算法。作为一种新的进化计算结构,它可以用来解决DE算法中的分布偏差问题。进化公式类似于仿射变换,如下所示:
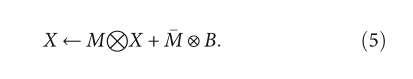
2.2.1. The Coevolutionary Matrix M
QUTARE算法认为群体中的所有搜索代理都具有相同的状态。通过这种协作结构,搜索代理之间可以相互协作,共享信息。首先构造初始矩阵Minitial,然后通过一系列变换得到协进化矩阵M。
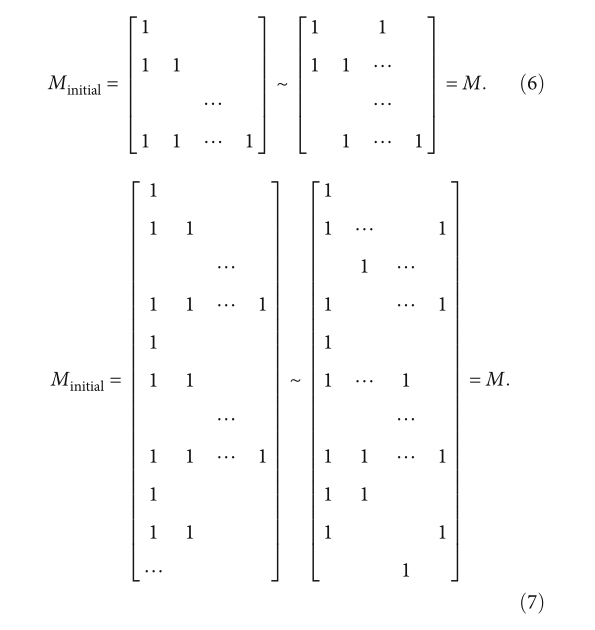
有三种构造MInitial的方法。具体的选择取决于种群大小PS和搜索空间维度D之间的大小关系。如果PS=D,则MInitial是D维的二进制下三角矩阵,如公式(6)所示。当PS>D时,MInitial需要扩展。如果PS=p∙D,则MInitial是Pd维二进制下三角矩阵垂直堆叠的矩阵。如果ps=p∙D+q,则根据前面的情况处理前p个∙D行,其余行取公式(6)中的前q行,如公式(7)所示。然后,对MInitial进行两步变换,即可得到M。首先,MInitial中每行的元素是随机排列的。然后,每个行向量的元素保持不变,而它们在矩阵中的位置是随机排列的。这样我们就能得到M:
2.2.2. The Donor Matrix B
施主矩阵B主导着进化的方式。与DE中的不同变异策略类似,生成B的方法有很多种。这里使用的模式称为Quatre/Best/1,如中所示:
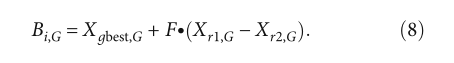
3. The Hybrid Algorithms Based on WOA and QUATRE (WOA-QT)
元启发式算法有两个基本元素:探索和利用。探索的任务是在搜索空间中尝试不同的解决方案,并试图找到全局最优解。开发的任务是在局部范围内搜索,充分挖掘当前最优解带来的优化机会。理想情况下,如果这两个阶段能够相互配合,实现平稳过渡,就可以避免局部最优,最终找到最优解[27]。
WOA已被证明优于一些高级优化算法,例如PSO、DE、GSA和快速进化编程(FEP)[28]。它提供了多种更新模式,努力平衡勘探和开发之间的关系。但不可避免的是,如何进一步提高勘探能力、释放开发潜力、避免局部最优等问题依然存在。局部最优停滞和收敛速度慢是它的两个主要缺点。为了提高算法跳出局部最优的能力,本文将Quatre算法引入到WOA中,并采用动态缩小搜索空间的策略来提高时间效率。在这一部分中,我们将详细分析问题产生的原因,并阐述相关的对策。
3.1. The Combination of WOA and QUATRE
虽然 WOA 有两种不同的利用模型,但它们都高度依赖于当前的最优值。当问题是多峰函数或复杂函数时,存在陷入局部最优的风险。如何处理这种情况需要仔细考虑。
Quatre是一种协同进化算法,采用矩阵模式计算,参数简洁。从统计学和概率论的角度来看,个体在进化过程中的运动方式更加合理。此外,算法中的协进化矩阵能够更全面地感知目标函数的结构,使得解空间的搜索更加有效。
基于上述考虑,本文提出了一种基于WOA和Quatre的混合算法。具体思路是在WOA的开发阶段嵌入Quatre。当前的最优解X∗?!FIt?在包围模式和气泡网攻击模式中都占据绝对主导地位。QUATRE算法可用于对当前最优解进行预处理,其效果相当于根据统计学和概率论对当前最优解进行扰动,弥补了当前最优解随机性和多样性的不足。两种算法在环绕模式下的融合方法如下:
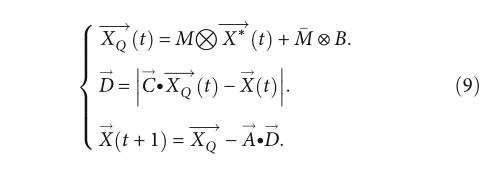
同样,在气泡网攻击模式下,也会进行两种算法的融合,如下式所示:
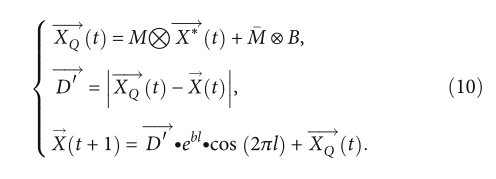
Quatre有不同的变异策略,它们强调搜索能力的不同侧重点[29,30]。模式QUATRE/BEST/1形式简洁,仅使用当前最优解XgBest,G和两个随机选择的解XR1和XR2。XgBest,G主导种群进化,使适应值较高的个体能够充分利用进行良好的局部搜索,收敛速度更快。虽然这两种算法的结合增加了种群的随机性,但为了避免过度纠错,我们选择了Quatre/BEST/1作为变异策略。因此,既保证了种群多样性,又考虑了收敛速度。
因此,既保证了种群多样性,又考虑了收敛速度。
3.2. Strategy of Dynamically Shrinking Search Space (DSS)
候选解应该逐渐逼近全局最优解。总的趋势是搜索空间的大小随着迭代的进行而减小。然而,WOA的搜索空间始终是初始化时的大小。在这样一个固定大小的空间中随意漫游显然是不合理的,这可能会导致优化过程的延迟。本文提出了一种动态缩小搜索空间的机制,并将其应用于WOA的探索阶段。随着优化的进行,随机解选择范围的上下限也会相应改变,使得搜索空间的大小逐渐减小,从而提高搜索效率。具体方法如下:
首先定义四个变量:新生成的搜索空间ub_new的上限、新生成的搜索空间lb_new的下限、当前迭代的最大解分量ub_max和当前迭代的最小解分量lb_min。上述变量的初始值是根据搜索空间的初始大小设置的。
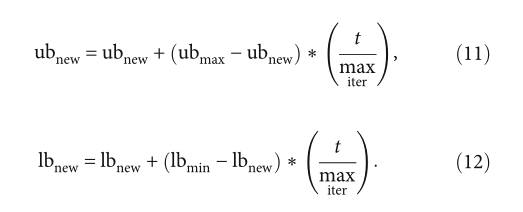
其中t表示当前迭代次数,max_iter表示最大迭代次数。随着迭代的进行,ub_new将根据公式(11)近似线性减小,而lb_new将根据公式(12)近似线性增加。其结果是,探索范围逐渐缩小,不断逼近全局最优解。现在,从由ub_new和lb_new定义的动态缩小的搜索空间中生成探索过程中的随机解。且收缩速度不过快,可有效避免局部最优停滞。
3.3. Hybrid Algorithm WOA-QT
本节介绍 WOA-QT 的优化步骤。伪代码如伪代码 1 所示。

(1)初始化:随机生成N个个体xi≠i = 0, 1, 2, 3,⋯,NÞ,形成种群x。初始值设置为WOA和QUATRE中的参数。
指定的最大数量的迭代马克斯_iter和参数相关搜索空间的大小(包括初始乌兰巴托上限和下限磅,ub_new上限和下限lb_新的搜索空间的每一次迭代后,最大的解决方案组件ub_最大和最小的解决方案组件lb_当前迭代)。
(2)评价:计算每个个体的适应度值f ðXiÞ。
通过相互比较,确定当前具有最佳适合度值的个体X∗。
(3)更新:选择一种方式更新个人的位置。
(i)勘探:当probb < 0:5且jAj≥1时,利用((2))式更新解。即在当前搜索空间(上限ub_new和下限lb_new之间)中随机选择一个解Xrand。
(ii) 开发 (A) 当 prob < 0:5 且 jAj < 1 时,使用等式 (9) 更新解决方案。这是嵌入QUATRE (B) B 的WOA 包围模式。当prob ≥ 0:5 时,使用公式(10)更新解。这是嵌入QUATRE的WOA泡泡网攻击模式
(4)再评价:对总体进行再评价,找出最优个体X-∗。并根据公式(11)和(12)缩小搜索空间的大小。
(5)终止:重复步骤(3)至(4)。如果已获得预定义的函数值或所有迭代均已完成,则记录全局最优解X∗ 及其最佳适应值fðX∗Þ. 优化过程在这里结束。
4. Experiment Results and Analysis
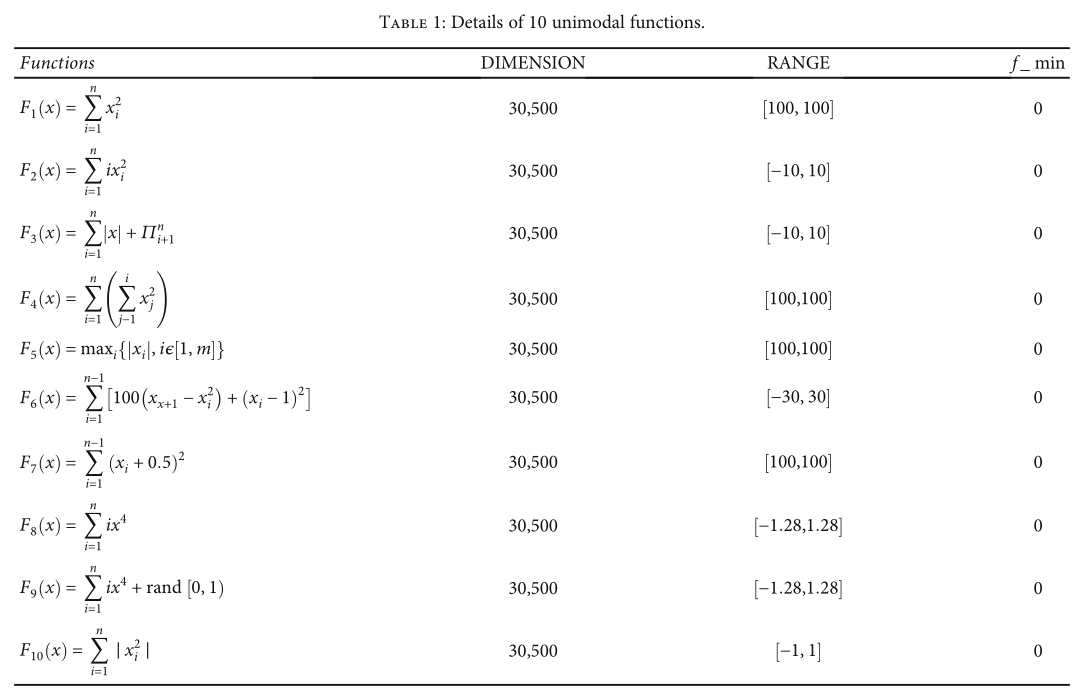
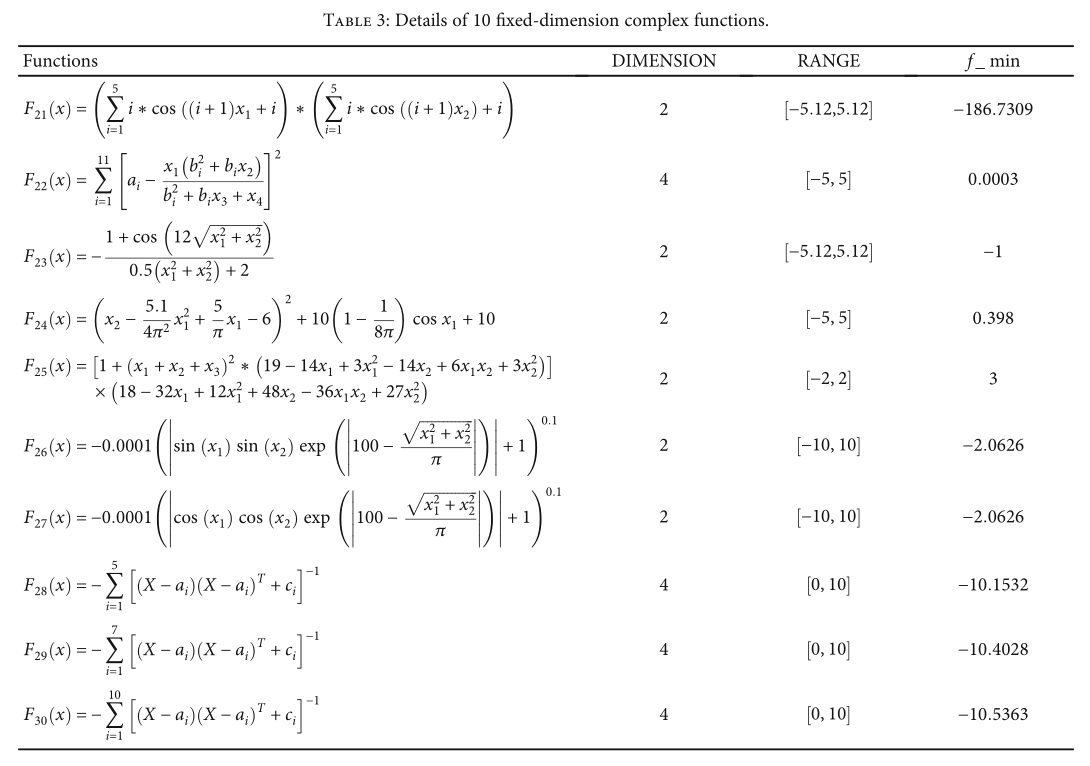
本部分选取了30个基准函数进行性能评价,如表1、表2和表3所示。大多数基准函数来自文献[31],包括三类:单峰、多峰和固定维复函数。我们还分别评估了该算法在解决低维和高维问题时的性能。所选择的单峰函数和多峰函数是覆盖低维和高维的可伸缩函数。所有实验都在WOA-QT、WOA和QUATRE之间进行了比较。每个算法独立运行40次。具体实验方案如下。

4.1. Experiments for Low-Dimensional Unimodal and Multimodal Functions
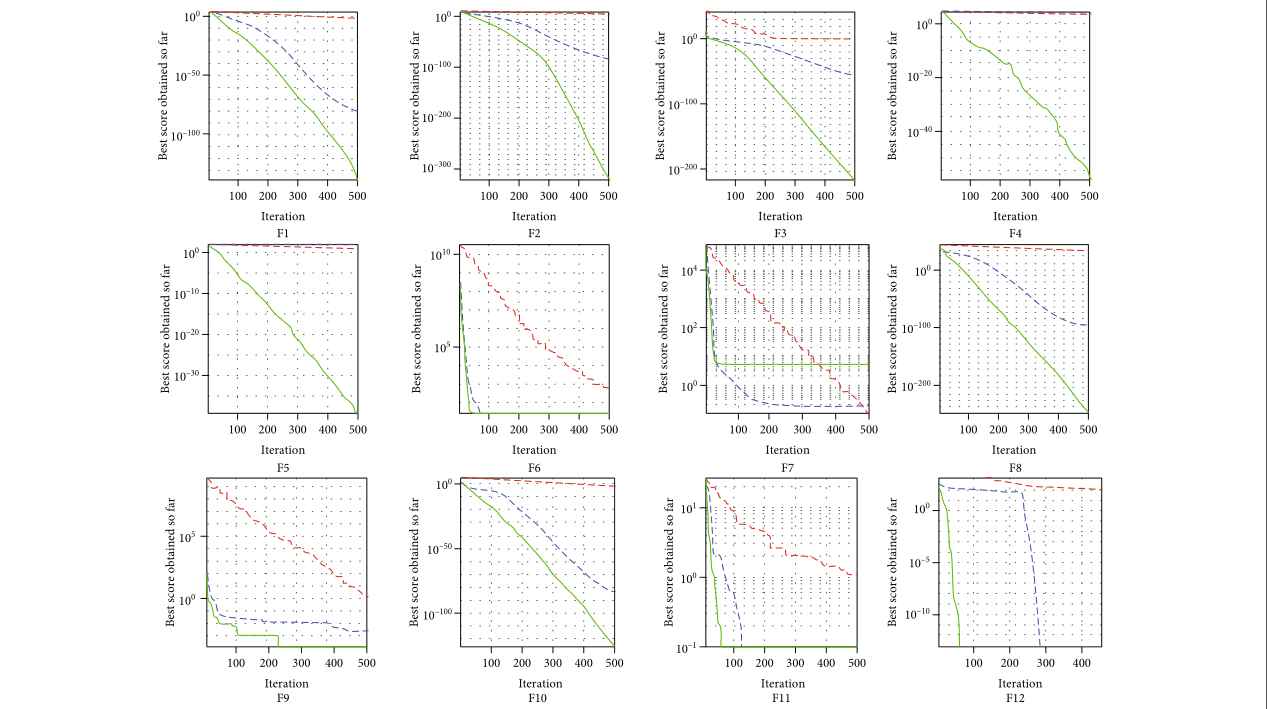
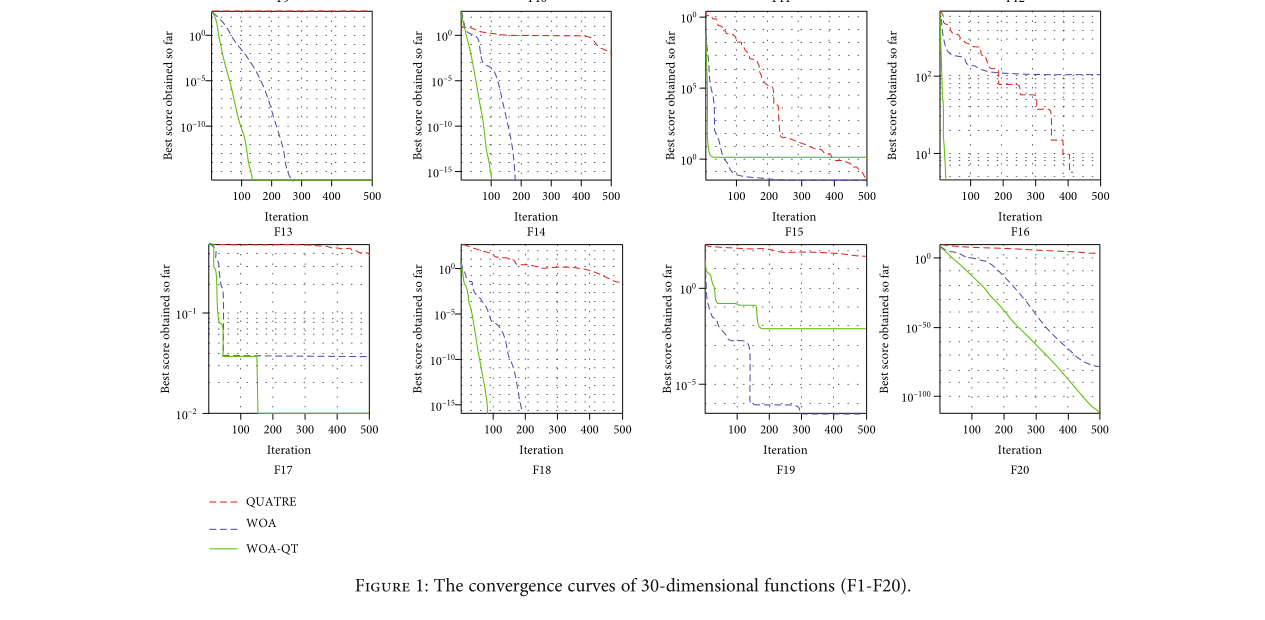
首先对低维单峰函数和多峰函数进行测试,维度设置为30。我们选择的比较指标包括每个实验的最小值(即最优值)、中值、最大值、均值和标准差值.图 1 显示了每个函数的收敛曲线。
在10个单峰函数的测试中,我们可以看到WOA-QT在9次(F1-F6、F8-F10)的最优值比较中都取得了第一名。与其他两种算法相比,WOA-Q的优化精度和收敛速度都有显着提高,表现出出色的局部搜索能力。此外,WOA-QT在其他统计数据的对比中也具有绝对优势,可见其性能稳定性远优于WOA和QUATRE。
从10个多模态函数的实验结果可以看出,WOA-QT在所有指标的排名中具有绝对优势。这表明它可以有效地避免陷入局部最优。
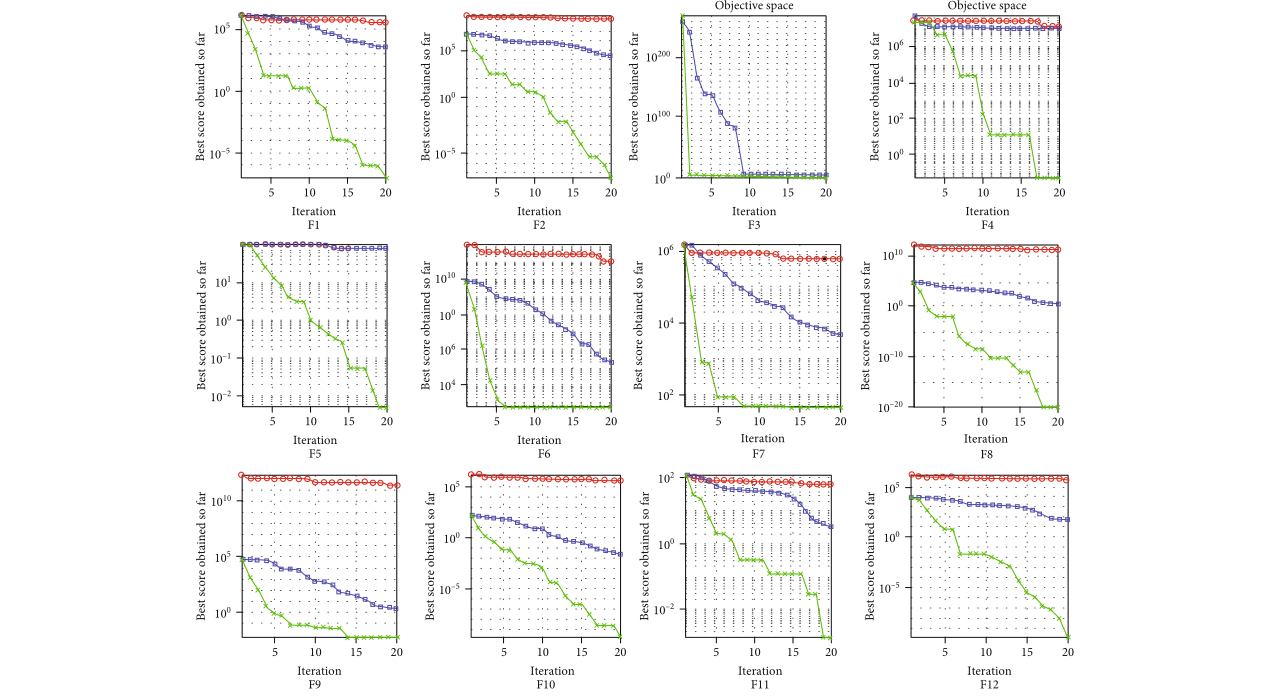
4.2. Experiments for High-Dimensional Unimodal and Multimodal Functions
本实验继续使用上一节中的测试函数,但将维度扩展到500。本实验的结论与上一次实验的结论基本一致。WOA-Qt在高维情况下仍然保持良好的性能。函数收敛曲线见图2。
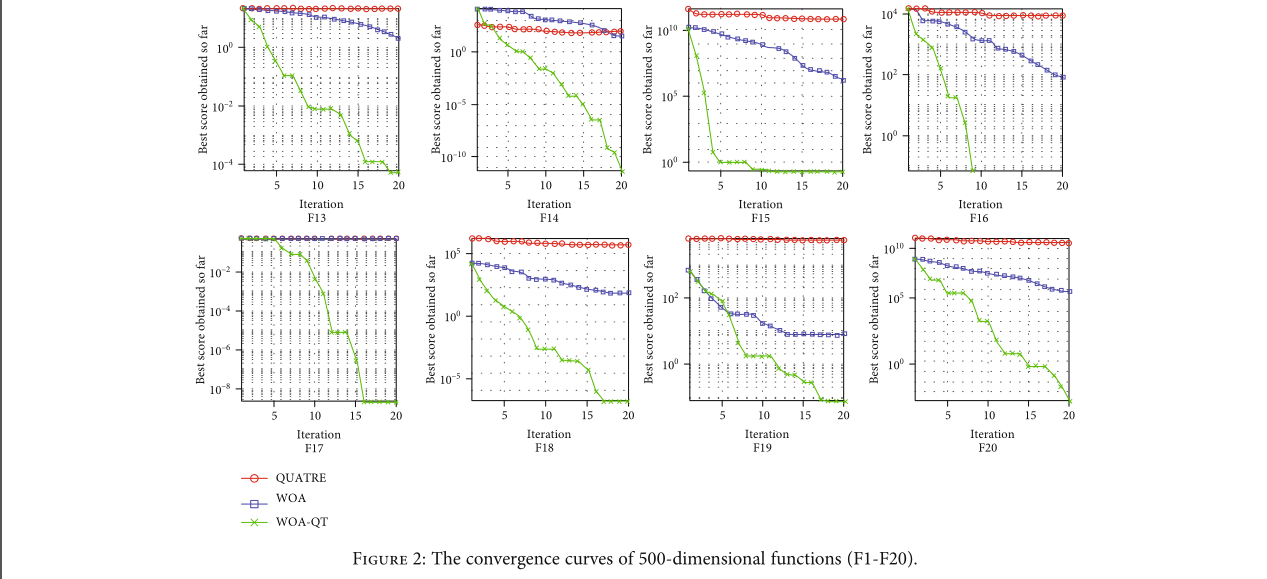
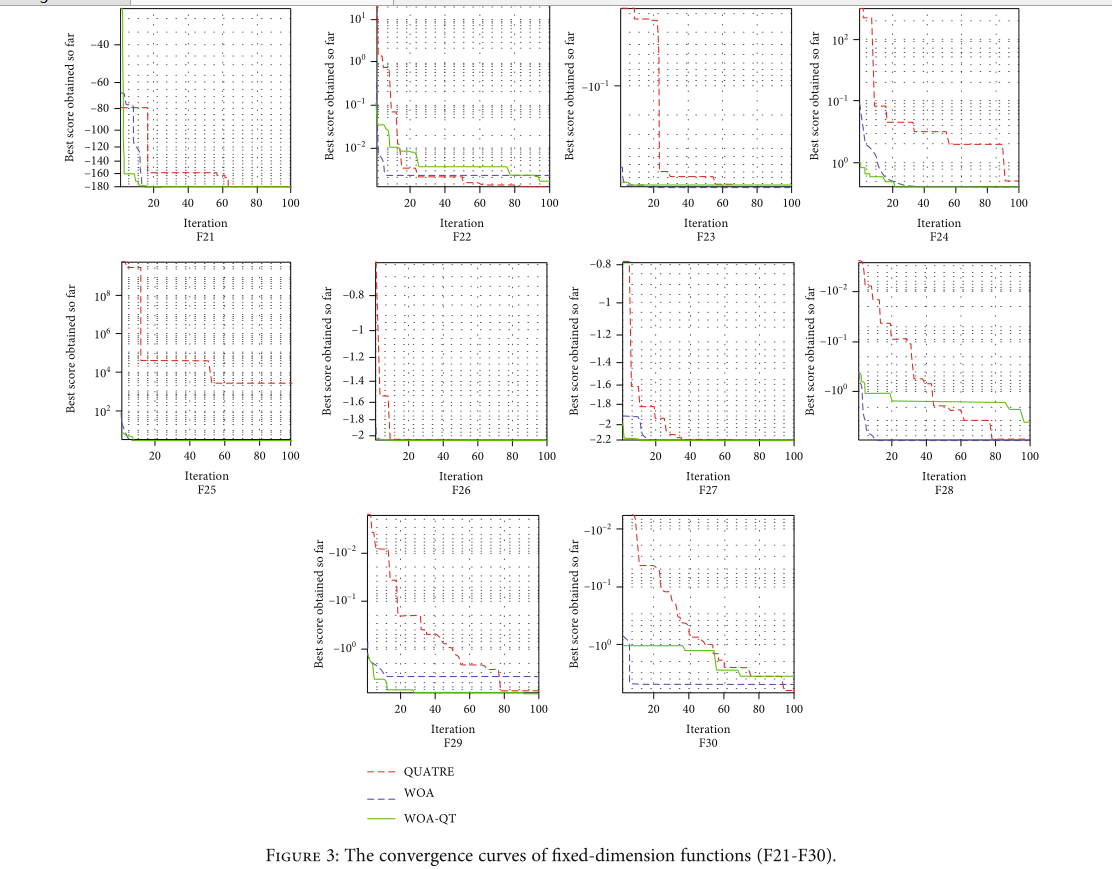
4.3. Experimental Results of Fixed-Dimension Complex Function
我们还测试了 10 个固定维度的复杂函数。发现WOA-QT的综合性能仍然是三者中最好的。图 3 显示了本实验得到的函数收敛曲线。
4.4. Analysis of Experiment Results
为了评价的科学性和公平性,本文选择了不同类型的基准函数进行测试。它还检查了算法解决可扩展维度问题的能力。
在解决单峰问题时,WOA-QT体现了突出的局部开发能力。面对多模态问题,可以很好地避免陷入局部最优。优化精度和速度都极大地受益于两种算法的有效混合机制。此外,当问题空间的维度扩大或缩小时,或者当问题逐渐复杂,计算量突然增加时,WOA-QT仍然保持着可靠的优化性能,尤其是具有令人满意的收敛速度。高时间效率证明了DSS策略的有效性。
5. Node Location in WSN
无线传感器网络、RFID、云计算、无线数据通信等共同构成物联网的技术基础。其中,无线传感器网络不仅是物联网感知层的重要信息采集主体,也是网络层的基本传输通道。在物联网中如何实现数据的智能感知、传输、处理和应用,无线传感器网络起着至关重要的作用。无线传感器网络的研究课题很多,其中节点定位一直是研究热点。由于位置信息未知的监测数据通常没有意义,而定位问题是大多数应用的基础和前提,传感器节点定位算法的性能直接影响其可用性。常用的评价指标包括定位精度、规模、节点密度和功耗。本文使用提出的WOA-QT算法来解决无线传感器网络中的节点定位问题。具体地说,就是将节点定位算法智能化,进一步提高定位精度。
虽然节点定位算法很多,但可以分为基于距离的节点定位算法和基于距离的节点定位算法。基于距离的定位算法通过测量距离或角度信息来计算未知节点的位置。常用的测距技术包括到达时间(TOA)、到达时差(TDOA)、指示器接收信号强度(RSSI)和到达角(AOA)。无距离定位算法只根据网络的连通性等信息确定节点位置,而不知道距离或角度。常用的方法有凸规划、DV-HOP、质心定位算法等。
不同的定位算法各有优缺点。本文采用的定位算法融合了RSSI测距算法和加权质心定位算法(WCL_RSSI),在一定程度上提高了定位精度。为了满足进一步减小定位误差的要求,本文采用提出的WOA-QT算法对WCL_RSSI进行优化。
5.1. RSSI Ranging Technology
RSSI测距方法的原理是将接收到的无线信号能量强度转换为节点之间的距离,然后利用它来估计未知节点的位置。由于不需要额外的硬件,成本和功耗相对较低,RSSI方法得到了广泛的应用,特别是对于大规模的WSN节点定位问题。
然而,距离和障碍物等环境因素会对无线信号的传输产生很大的影响,导致信号的功率强度严重衰减。本文选择对数距离分布模型作为无线信号传播路径损耗的距离测量模型,如下所示:
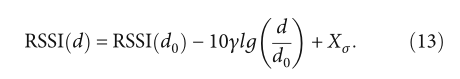
为了将 Di 转换为 N 和 Si 之间的欧几里得距离 ρi,这需要知道两个距离之间的近似比例关系。假设两个信标节点Si和Sj之间的连接距离为Di,j(可以通过RSSI测距得到),欧式距离为
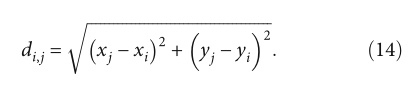
我们将αi定义为信标节点Si的路径比例因子,如下图:
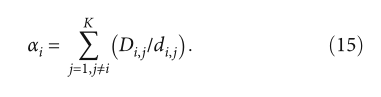
显然,距离 ρi 可以通过以下公式获得:

5.2. Weighted Centroid Location Algorithm Based on RSSI (WCL_RSSI)
不难看出,如果仅靠RSSI测距定位,精度较差。因此,一种基于RSSI的加权质心定位算法应运而生。普通的质心定位算法认为所有信标节点的状态是平等的。事实上,不同的信标节点对未知节点的定位有不同的影响。WCL算法是通过权重因子来反映每个信标节点对质心(即未知节点)位置的影响程度。这里使用的是三角形质心定位算法。未知节点与三个信标节点之间的成对距离被记录为(ρ1、ρ2和ρ3),它们用于构造权系数。相关公式如下:
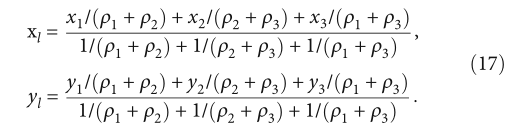
WCL_RSSI具有计算复杂度低、实现简单、定位精度高等优点。此外,定位过程受传输环境变化的影响较小,不需要节点之间的交互[32]。
5.3. Apply the Proposed WOA-QT Algorithm to WCL_RSSI
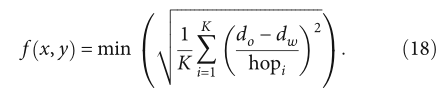
有 K 个信标节点。信标节点Si和未知节点之间的跳数记为hopi。等式(18)表示优化目标,即最小化两个距离之差的均方根误差。
5.4. Simulation Results
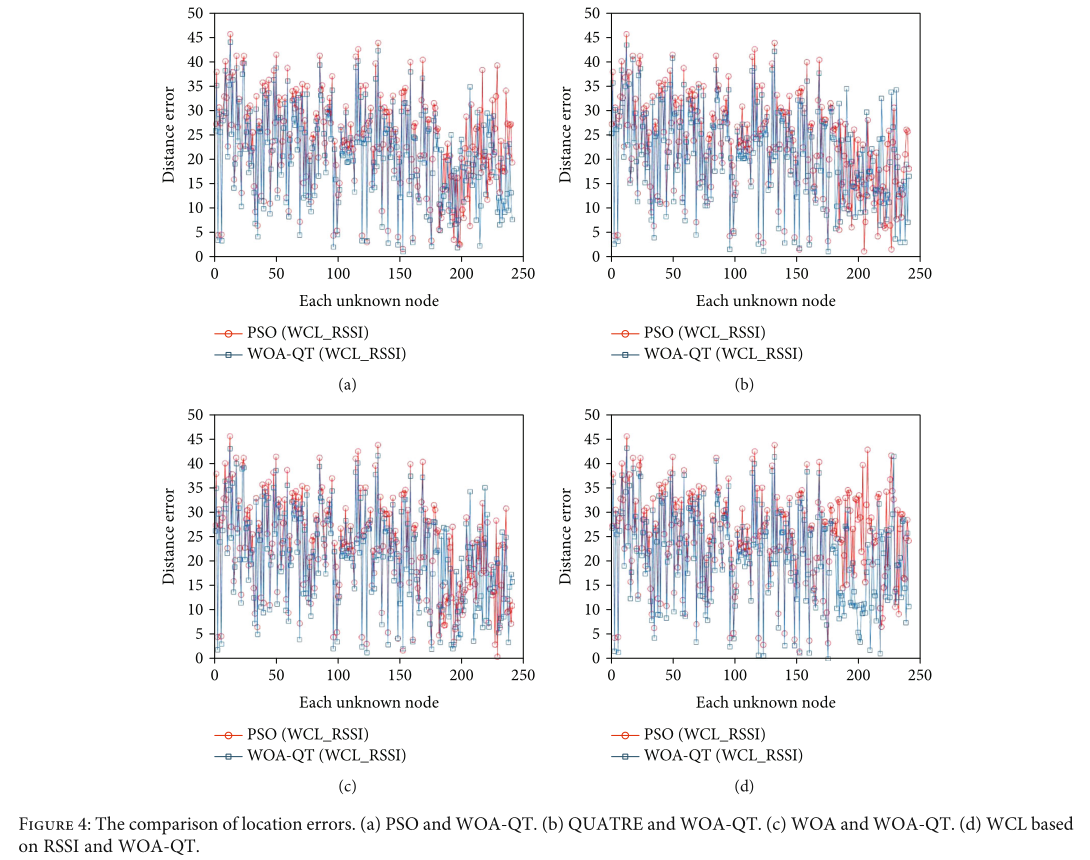
假设在 1000 m×1000 m 的二维区域内,部署了 60 个信标节点,需要确定 240 个未知节点的位置。传感器节点的通信半径为15米,算法最大迭代次数为400次。表4列出了每种算法估计的未知节点位置与真实位置的平均距离误差。仿真实验涉及五种算法。仿真结果表明,基于WOA-QT的WCL_RSSI误差最小,定位精度明显提高。为了可视化定位误差,图 4 标出了每个未知节点的估计位置与其真实位置之间的距离偏差。
6. Conclusion
AI和IoT是兼容和共生的,他们天生就是最好的合作伙伴。它们突破了各自并行发展的瓶颈,实现了高频共振和协调发展。
本文将人工智能中的优化算法用于解决物联网的关键技术--无线传感器网络中的节点定位问题。涉及到两种优化算法:WOA算法和QUATRE算法。WOA源于自然智慧,QUARTRE具有数学之美。这两种算法相互利用,紧密合作,形成一个有机整体。整体优化性能远好于两者分离时的优化性能。通过相互融合进一步挖掘局部开发潜力,有效避免了搜索全局最优解过程中的局部停滞。虽然算法杂交不可避免地会带来更多的计算量,但是在两种算法和DSS策略的配合下,算法的时间效率并没有受到影响,在很多情况下甚至更好。因此,增加该算法的复杂度是值得的。在优化技术的帮助下,无线传感器网络的节点定位精度得到了显著提高。可以说,实现了一个具有应用价值的AIoT成功案例。
Quatre算法有许多变体。当与其他算法结合时,我们可以考虑如何自适应地选择不同的变体[33]。此外,算法杂交带来的复杂性可以考虑使用代理辅助技术来缓解[34,35]。在无线传感器网络领域,有许多具有挑战性的问题需要克服[36,37]。它可以与机器学习[38-40]等其他AI技术相结合,推动更多AIoT应用场景的诞生。

 基于混合优化算法的无线传感器网络节点定位方法
基于混合优化算法的无线传感器网络节点定位方法

