An Improved PSO Algorithm for Distributed Localization in Wireless Sensor Networks
An Improved PSO Algorithm for Distributed Localization in
Wireless Sensor Networks
一种改进的粒子群算法在无线传感器网络分布式定位中的应用
文章信息
博客内容仅用于学习。
Hindawi Publishing Corporation
International Journal of Distributed Sensor Networks
Volume 2015, Article ID 970272, 8 pages
http://dx.doi.org/10.1155/2015/970272
Dan Li1 and Xian bin Wen2
1School of Computer Science and Technology, Tianjin University, Tianjin 300072, China
2Key Laboratory of Computer Vision and System, Ministry of Education, Tianjin University of Technology, Tianjin 300384, China
Correspondence should be addressed to Dan Li; luyaocyan@163.com
Received 17 October 2014; Accepted 8 January 2015
Academic Editor: Chang Wu Yu
Copyright © 2015 D. Li and X. B. Wen. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
0. Abstract
无线传感器网络中的许多应用都要求对随机部署的节点进行准确、快速的定位,并将其归结为一个多维优化问题。粒子群优化算法(PSO)收敛速度快,对计算资源要求适中,适用于定位问题。本文提出了一种分布式两相粒子群算法来解决翻转歧义问题,提高了算法的效率和精度。本文采用包围盒方法定义初始搜索空间,并提出一种精化阶段来校正由于翻转歧义引起的误差。此外,我们的研究还尝试对只有两个引用或三个近共线引用的未知节点进行局部化处理。
仿真结果表明,本文提出的分布式定位算法优于以往的定位算法。
1. Introduction
可以协同感知环境的分布式自治节点网络称为无线传感器网络(WSN),在危险环境探索,军事目标跟踪和监视,健康监测和家庭自动化等场景中具有很大的应用潜力。在大多数这些应用中,支持许多其他网络服务的传感器节点的位置信息是至关重要的。
到目前为止,已经根据不同的应用需求提出了各种各样的定位方法,大致可以分为两种类型:基于范围的和无范围的。无测距算法主要利用传感器节点之间的连通性来估计未知节点的位置,无需任何测距技术。基于范围的算法使用一些测距技术 [1],例如到达时间 (TOA)、到达角 (AOA)、到达时间差 (TDOA) 和无线电信号强度 (RSS) 来测量未知节点之间的距离或角度和在测量测距信息后,它们的相邻锚节点将定位问题表述为多维优化问题。同时,它提供了比无范围算法更准确的定位结果。与经典优化方法相比,模拟退火算法(SAA)、遗传算法(GA)和粒子群优化(PSO)等仿生优化算法通过基于种群的技术来解决定位问题。它们具有更高的性能,并且具有更少的计算资源。其中,PSO是一种基于群体智能的进化计算方法,不使用交叉、变异等进化算子。它是一种高效的全局优化算法,具有操作简单、避免局部极小值的优点。许多文献应用仿生算法来实现 WSN 中的节点定位。
在[2]中提出了一种基于模拟退火的无线传感器网络定位算法,该算法使用大量锚节点来定位所有未知节点。根据性能评估,这种方法的准确性不如[3]中的PSO算法。 [4, 5] 中提出的用于 WSN 的两阶段定位算法是集中式的,不适用于大规模传感器网络。在 [4] 中提出的使用 SAA 和 GA 组合的定位算法具有三个或更多相邻锚点的未知节点。在文献[9]中,基于测距误差的概率分布,提出了一个新的目标函数来评价粒子的适应度。文献[10]将节点定位问题推广到三维空间。
我们提出了基于 PSO 的算法,该算法也可以扩展到大规模传感器网络。本文的主要贡献有以下两个方面。
(1)通过边界框方法减少初始搜索空间以加快收敛速度。
(2)提出分布式两阶段PSO算法,解决翻转模糊问题,定位更多目标节点。
本文的其余部分组织如下。第二部分对粒子群算法的理论和应用进行了综述。第三部分介绍了我们改进的粒子群算法在无线传感器网络分布式定位中的应用。第四节进行了仿真和分析。第五节对本文进行了总结,并对下一步的工作进行了展望。
2. Particle Swarm Optimization Algorithm
2.1. The Theory of PSO Algorithm
(基础知识,不再赘述)
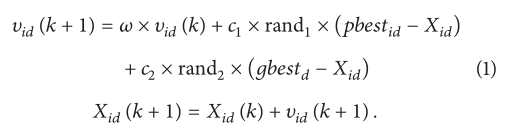
2.2. The Application of PSO in WSN Localization
粒子群算法(PSO)是一种基于范围的优化算法。在具有已知位置的传感器节点(称为信标)和其他需要本地化的传感器节点(称为目标节点)之间。我们将整个传感器网络和传感器节点分别视为二维坐标系和坐标点。
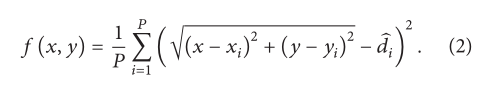
目标节点稳定下来并在下一次迭代中充当信标,并且重复定位过程,直到所有目标节点稳定或者没有更多的节点可以被定位。
在这个过程中的主要问题是由于近共线信标引起的翻转模糊,这在下一节中已经得到了很好的解决。在保证精度的前提下,通过减小初始搜索空间,减少了计算时间。
3. An Improved PSO Algorithm
在本节中,描述了一种基于范围的无线传感器网络分布式定位算法。经典 PSO 算法与我们提出的算法之间的差异。
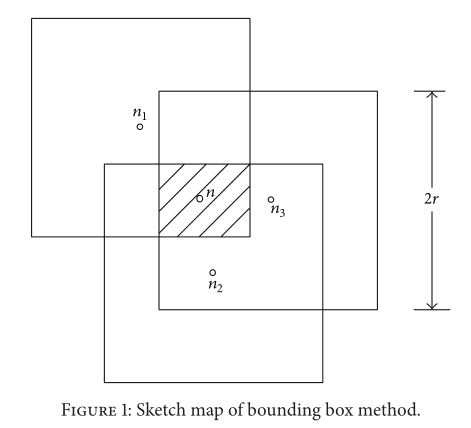
3.1. Define the Initial Search Space by Bounding Box Method
经典的 PSO 算法在搜索空间内采用一组可行的解决方案,称为具有随机初始位置的粒子群。在我们提出的算法中,我们通过使用边界框方法减少了初始搜索空间。在我们提出的算法中,每个目标节点都有由其传输范围内的参考(信标或固定节点)确定的唯一搜索空间。与经典PSO算法使用整个解空间作为所有目标节点的初始搜索空间相比,该算法减少了计算时间,减少了翻转歧义的可能性。
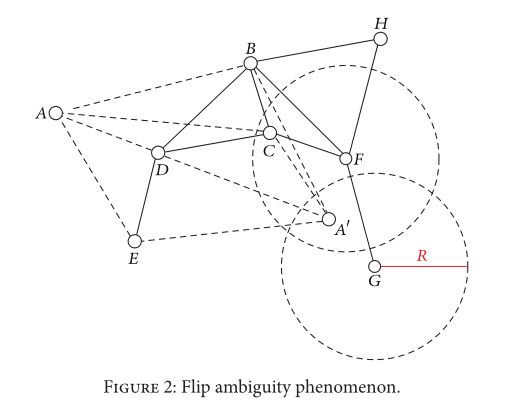
3.2. Anticipation of Nearly Collinear References
翻转模糊现象的例子(Figure 2)。
参照物越多,发生翻转歧义的概率就越小。因此,当参考文献数量较少时,我们应该使用以下规则来预测这些参考文献是否接近共线。
(i) 如果只有三个引用,则其中任何两个都不能使用。当任何两个参考之间的距离小于预定义的阈值时,这些参考被判断为接近共线。
(ii) 计算任何一个参考点到由任何两个参考点确定的直线的距离。当该值小于预定义的阈值时,这些参考被判断为接近共线。
在接下来的迭代中,目标节点可能有更多的引用,并且将被本地化,直到它的新引用被判断为非近共线。
3.3. A Refinement Phase to Correct the Error due to Flip Ambiguity
细化阶段是对预期阶段之后仍然存在翻转歧义问题的节点进行重新定位。为了检查是否发生了翻转歧义,我们使用了非邻居节点。
在细化阶段,对于那些局部化的节点落在错误的邻域内,我们会在目标函数(2)中添加一个额外的项(3),以便为新的估计引入额外的代价。
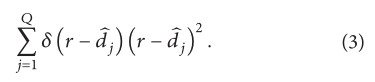
3.4. Localize the Target Nodes That Only Have Two References or Three Near-Collinear References
将至少有3个非近共线参考的目标节点全部定位后,剩下的只有2个或3个近共线参考的目标节点最后可以通过细化阶段进行定位。
3.5. Algorithm Steps
WSN节点定位的主要目的是通过使用具有已知位置的M信标以基于分布式范围的方式尽可能估计N目标节点的位置。
我们提出的方法的流程如下:
(i) N 目标节点和 M 信标随机部署在二维传感器场中。目标节点和信标的传输半径均为 r。信标具有位置感知能力并经常传输其坐标。在操作结束时完成的目标节点在下一次迭代中充当信标。
(ii) 落在三个或更多非近共线参考传输范围内的目标节点被认为是可定位节点。
(iii) 从可定位节点到其每个相邻参考点的测量距离被模拟为实际距离加上高斯加性白噪声。
(iv) 每个可定位节点运行改进的 PSO 算法,通过找到使目标函数 (2) 的值最小化的坐标 (x, y) 来定位自己。
(v) 在细化阶段,由于估计位置落入错误的邻域,应通过向目标函数 (2) 添加额外项 (3) 来重新定位在上一步中定位的一些节点。
(vi) 重复上述步骤,直到所有目标节点都已解决或无法定位更多节点。
(vii) 将至少有三个非近共线参考的目标节点全部定位后,剩下的只有两个或三个近共线参考的目标节点最后可以通过细化阶段进行定位。
(viii)
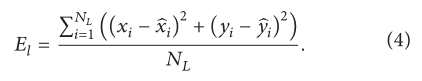
4. Simulation and Analysis
4.1. Compared with the Classical PSO Algorithm
提出的节点定位算法的参数设置如下:

为了更直观地展示我们算法的优势,我们制作了一些对比图来独立分析每个步骤,如下所示。
首先,我们使用3.2和3.3节中描述的方法来避免翻转歧义现象。试验中的一个例子显示了在使用和不使用方法3.2和3.3的实验之间的不同定位结果。
如图3所示(红圈表示信标节点的位置,蓝圈表示目标节点的位置,蓝色星号表示PSO算法估计的位置,蓝色直线表示定位误差,即实际节点位置与估计位置之间的距离),翻转模糊现象会导致较大的定位误差。为了避免此类问题,我们使用3.2和3.3节中描述的方法进行重新定位。因此,在图4中纠正了较大的本地化错误。
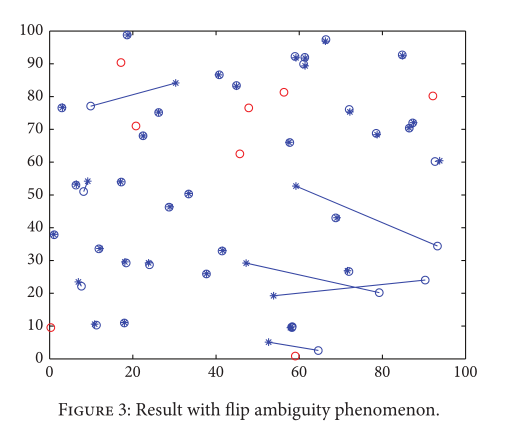
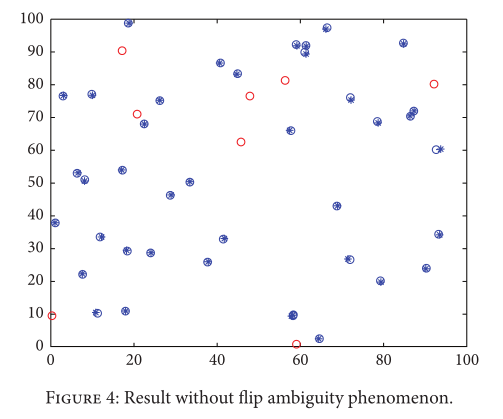
图 5 直接从纯数字角度显示了差异。
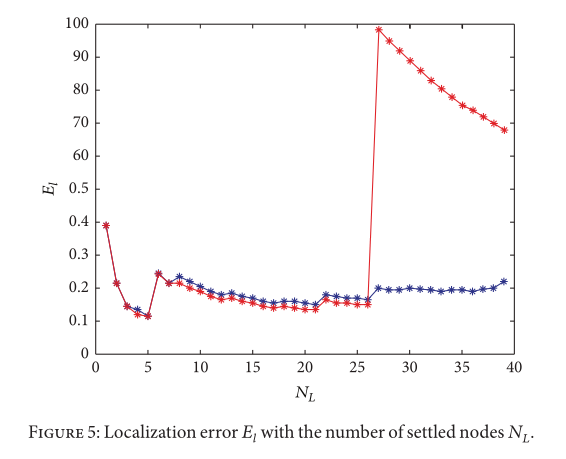
其次,我们通过使用 3.1 中描述的边界框方法来减少初始搜索空间。
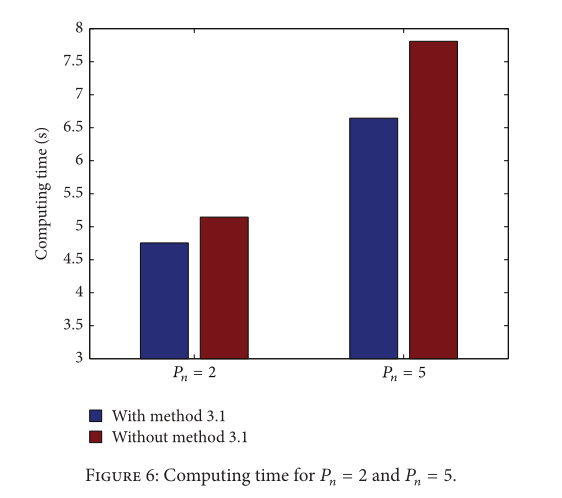
最后,在我们的算法中,我们通过使用最后在 3.4 中描述的细化阶段来定位只有两个参考或三个近共线参考的目标节点。
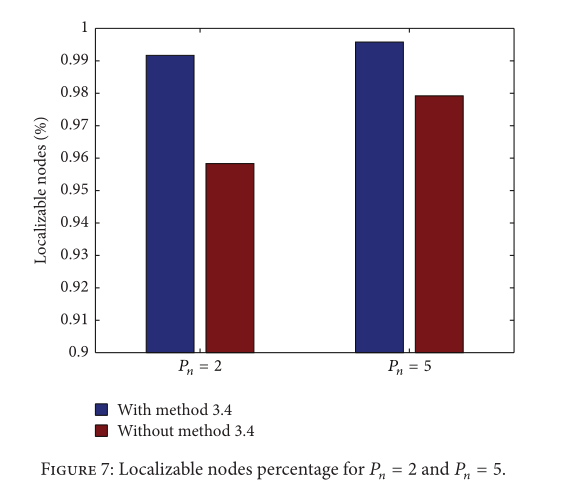
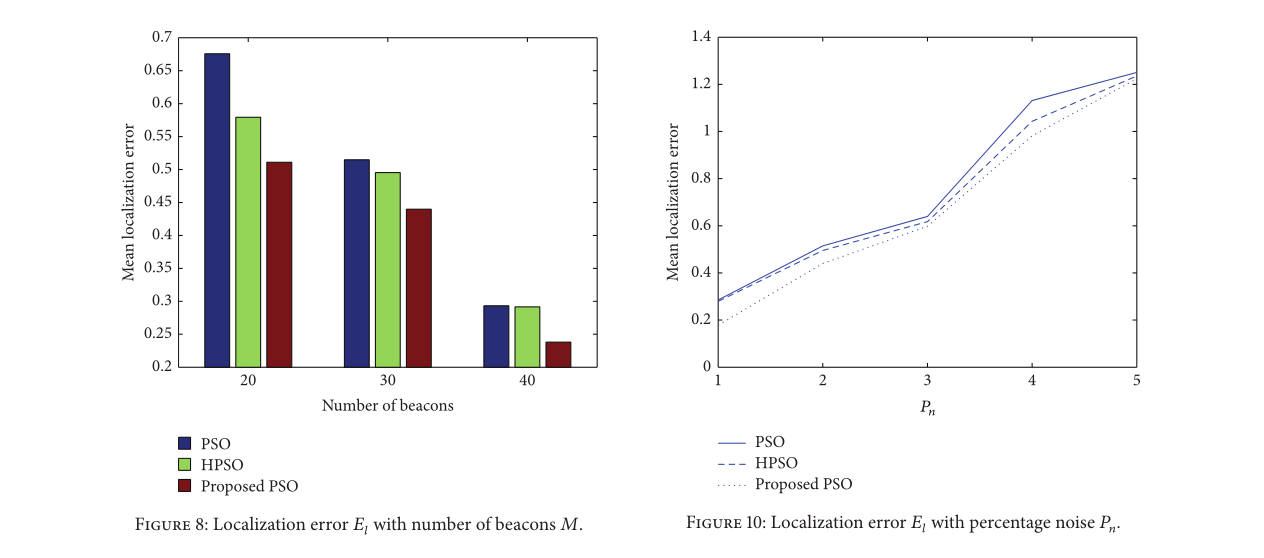
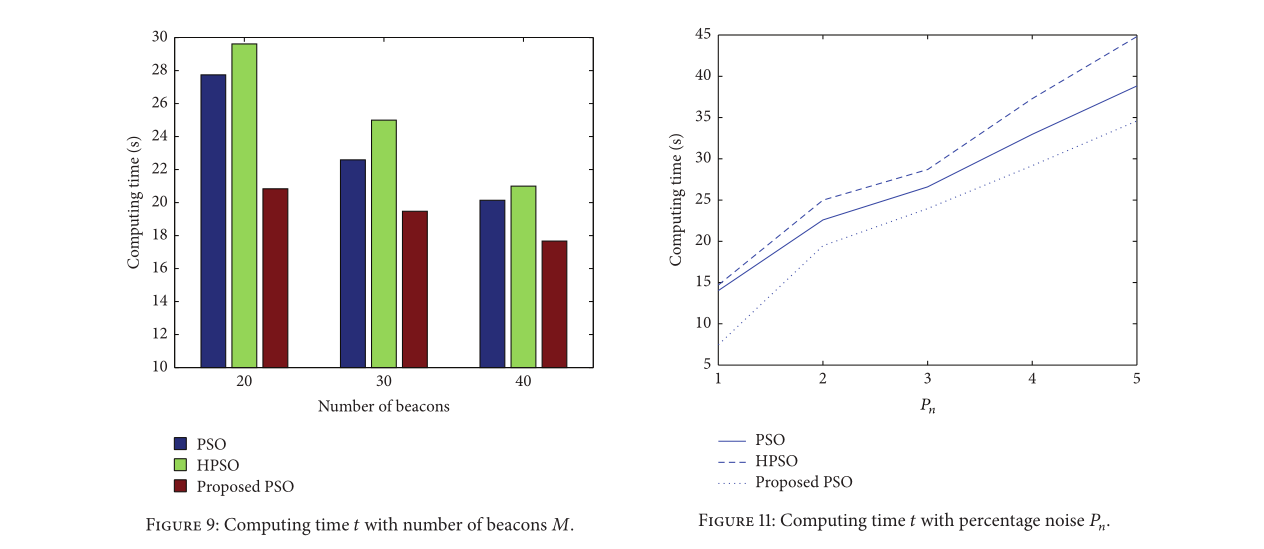
4.2. Compared with the HPSO Algorithm
HPSO方法[8]将整个群分成多个子群,局部群中适应度最好的粒子称为lbestid。
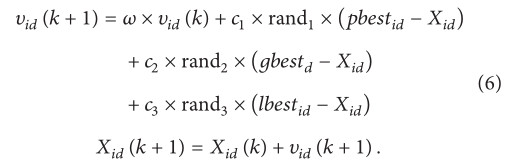
5. Conclusion and Future Work
针对无线传感器网络中的分布式定位问题,提出了一种改进的粒子群优化算法,该问题可以看作是一个多维优化问题。为了提高定位精度和算法效率,我们在第三节提出了一些方法,仿真结果证明了这些方法的有效性。为了更直观地显示算法的优势,我们制作了对比图,分别对每种方法进行了分析。实验结果表明,该方法能够在较少的计算时间内以较高的精度定位出更多的未知节点,优于其他两种方法。
进一步地,迭代误差传播和能量消耗的控制是一个很有潜力和重要的方向。在本文中,我们考虑了二维空间中的节点定位问题。然而,在现实环境中,传感器节点分布在三维空间中。一些基于我们提出的算法的研究将被应用于三维空间。此外,该算法还可以扩展应用于移动无线传感器网络中的节点定位。这些规划工作的成效将在未来的实验中得到验证。

 一种改进的粒子群算法在无线传感器网络分布式定位中的应用
一种改进的粒子群算法在无线传感器网络分布式定位中的应用

