C++之分治算法
C++之
分治算法篇
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。
基本思想:
当我们求解某些问题时,由于这些问题要处理的数据相当多,或求解过程相当复杂,使得直接求解法在时间上相当长,或者根本无法直接求出。对于这类问题,我们往往先把它分解成几个子问题,找到求出这几个子问题的解法后,再找到合适的方法,把它们组合成求整个问题的解法。如果这些子问题还较大,难以解决,可以再把它们分成几个更小的子问题,以此类推,直至可以直接求出解为止。这就是分治策略的基本思想。一般情况下,还会用到二分法。
二分法:
利用分治策略求解时,所需时间取决于分解后子问题的个数、子问题的规模大小等因素,而二分法,由于其划分的简单和均匀的特点,是经常采用的一种有效的方法,例如二分法检索。
基本算法:
分治法解题的一般步骤:
if(1、问题不可分)2、返回问题解;
else
{
3、从原问题中划分出含一半运算对象的子问题1;
4、递归调用分治法过程,求出解1;
5、从原问题中划出含另一半运算对象的子问题2;
6、递归调用分治法过程,求出解2;
7、将解1、解2组合成整个问题的解;
}
}//结束
相关例题:
问:
设有n=2^k个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表:
(1)每个选手必须与其他n-1个选手各赛一次; (2)每个选手一天只能参赛一次; (3)循环赛在n-1天内结束。
请按此要求将比赛日程表设计成有n行和n-1列的一个表。在表中的第i行,第j列处填入第i个选手在第j天所遇到的选手。其中1≤i≤n,1≤j≤n-1。8个选手的比赛日程表如下图:
解:
#include<iostream>
#include<cmath>
using namespace std;
#define MAXN 64
int calendar[MAXN + 1][MAXN];
void Round_Robin_Calendar()
{
int i,j,m,number,n,temp,t=0;
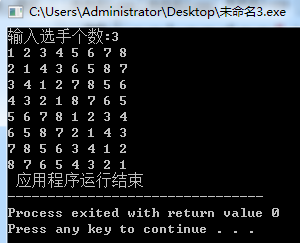
cout<<"输入选手个数:";
cin>>number;
n= 2;
calendar[1][1] = 1; calendar[1][2] = 2;
calendar[2][1] = 2; calendar[2][2] = 1;
for(m=1;m < number;m++)
{
temp = n;
n=2*n;
for(i = temp + 1;i <= n;i++)
for(j = 1;j<= temp ;j++)
calendar[i][j] = calendar[i - temp][j] + temp;
for(i = 1;i <= temp;i++)
for(j = temp + 1;j <= n;j++)
calendar[i][j] = calendar[i + temp][(j +temp)%n];
for(i = temp+1;i<= n;i++)
for(j=temp+1;j<= n;j++)
calendar[i][j] =calendar[i-temp][j-temp];
}
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{ cout<<calendar[i][j]<<" ";
t++;
if(t%8==0)
cout<<endl;
}
}
int main(int argc, char* argv[])
{
Round_Robin_Calendar();
cout<<" 应用程序运行结束 ";
return 0;
}