CS231N assignment 1 _ 两层神经网络 学习笔记 & 解析

two layer net

神经网络的定义

我之前看到的神经网络对于各个层和激活函数的各种表达的总是不够清晰. 所幸本课程对于网络具体细节总算有了严格的定义. 我们实现的是包含ReLU激活函数和softmax分类器的网络. 下面是简单的图形示意: (应该足够清晰了)

需要注意, 输出层之后是没有ReLU的. 在实际推演中, 我们操作的是矩阵. 我们以500张图片向量输入为例:

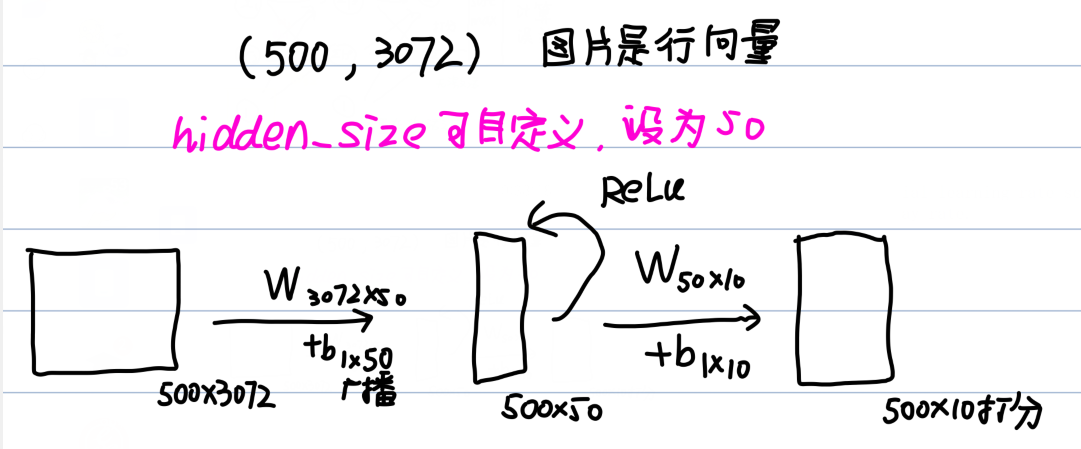
因此不难看出, 这和我们之前的softmax分类器区别仅仅是线性分类器变成了线性+非线性+线性组合的网络. 这样, loss计算只需要照抄前面的softmax计算得分loss的非循环版本即可. 下面是前向推演的代码:

h1 = np.maximum(0,X.dot(W1) + b1) # relu(x) = max(0,x)
scores = h1.dot(W2) + b2

计算误差的代码. 需要注意,为了减少计算时间, 我们需要尽可能优化算法, 用到之前已经求出的变量,发现其中的关系!!

        out_scores = scores - np.max(scores,axis=1).reshape((-1,1)) # -1表示自动决定,正则化
        softmax_output = np.exp(out_scores)/np.sum(np.exp(out_scores),axis=1).reshape(-1,1) # 计算softmax识别. 因为本质上只是算y的
        #误差,所以直接用-log(softmax_y输出)表达即可.前面的代码没有用过这中方式,会复杂一些.记录一下
        loss = -np.sum(np.log(softmax_output[np.arange(N),y])) # -log求解
        loss/=N
        loss+= 2*reg*(np.sum(W1*W1)+np.sum(W2*W2))

反向传播

前向推导梯度下降才是最困难的.我们需要求解的是dW2,db2,dW1,db1这四个参数. 下面我们开始求解: 

为了保证推导可以转化成代码,我们需要确认以下事项:

• 结合矩阵规模和表达式, 确认转置等. 对于广播的b, 反向还需要求和.
• 列出表达式之后,注意和前面推导和各层特点的关系.
• 别忘了正则化项.

好了, 有了上面的基础, 我们就写出了最终代码:

dS4 = softmax_output.copy() # 注意直接dscores = softmax_output是不行的,我们需要用copy方法深拷贝.求出dS4
        dS4[range(N),list(y)]-=1 
        dS4/=N # loss需要/N以确保梯度下降幅度不致因为样本数量太大而下降过快
        # 之后照抄上面的推导过程即可
        grads['W2'] = h1.T.dot(dS4) + 2*reg*W2 # S3就是隐含层输出
        grads['b2'] = np.sum(dS4,axis=0) 
        dS3 = dscores.dot(W2.T)
        dS2 = (h1>0)*dS3
        grads['W1'] = X.T.dot(dS2) + 2*reg*W1
        grads['b1'] = np.sum(dS2,axis = 0)

 最终验证通过:

下面是训练过程,也是之前的东西:

idx = np.random.choice(num_train,batch_size,replace =True)
            X_batch = X[idx]
            y_batch = y[idx]
    #...
            self.params['W2'] += -learning_rate * grads['W2']
            self.params['b2'] += -learning_rate * grads['b2']
            self.params['W1'] += -learning_rate * grads['W1']
            self.params['b1'] += -learning_rate * grads['b1']
    # predict
            scores = self.loss(X)
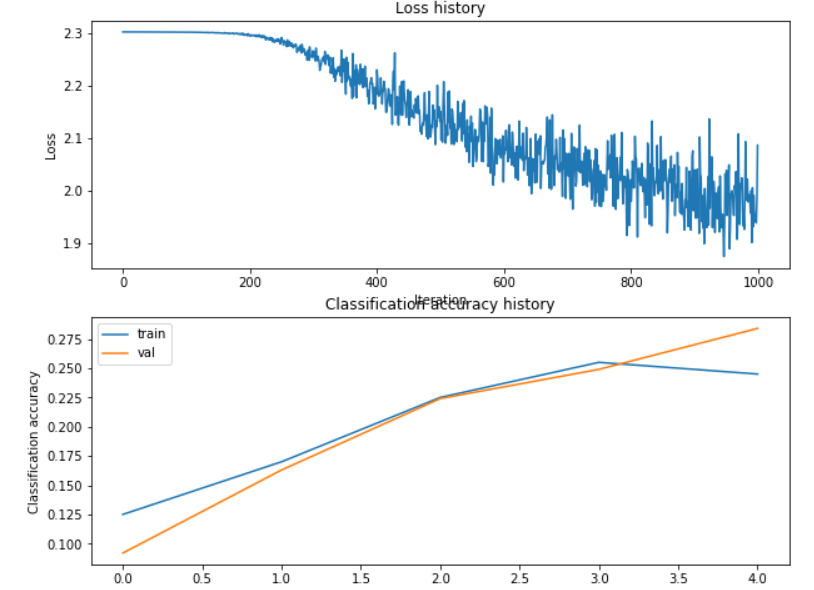
            y_pred = np.argmax(scores, axis=1)

结果先不放了, 我们通过CIFAR10再来看具体情况. 很抱歉, 在默认的参数下, 可以说效果极其不好(loss压根不收敛<虽然已经比KNN强了/doge>):

调参

这里的超参数是reg和lr,以及隐含层元素个数.(其实还有神经网络层数等,不过不是本作业的讨论范围了) . 我们认真分析可知:

a. 模型有明显的欠拟合. 这个或许是Reg太大了,也有可能是隐含层元素个数太少了.

b. 前期的下降很慢, 且仍然有下降趋势, 可以适当提升lr.(千万不要以为loss波动就感觉lr可能大了)

c. 除此之外, 我们还可以尝试调整迭代次数.

为此, 我们不妨探究不同的超参数单独应用下的变化趋势,查看收敛的最终成果最后根据需要调节lr的值.

务必注意: 在实现代码中, net = TwoLayerNet(input_size, hidden_size, num_classes)必须写在for循环内, 否则权重初始值很容易直接给网络梦幻开局, 导致准确率虚高.

(下面的试验lr=1e-3<这是其他博客的最优结果>,迭代次数1000)

 

 

 从此我们就看出, lr才是影响最大的因素, 虽然看前面的loss history我们感觉波动很大, 但是实际上却依然存在下降的趋势, 所以应该提升Lr大小, 哪怕什么都不做准确率也能到达47%. 而我们回来看隐含层元素个数, 可以知道随着数量上升,整体趋势是上升的, 但是在120之后就有了瓶颈, 且训练耗时明显变长(后面会看到还不如花在提升迭代次数上), 为此我们选择个数为150.

下面是对reg正则化参数的探索. 默认的reg参数是否偏大? 为此, 我们从0-0.3拆分了11组数据尝试:

 

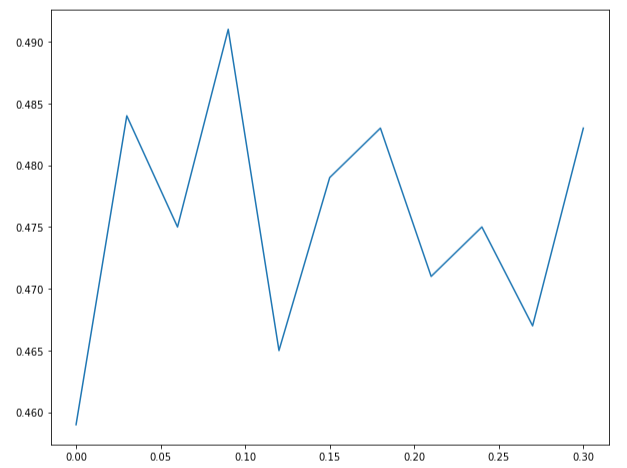
可以看出,在reg太小容易过拟合, 而reg较大整体趋势是下降的,所以我们初步认为在reg=0.09处的准确率最好. 辅以更大的迭代次数,准确率最终可以达到55%左右.为此我们再适当提高lr至0.002,设置迭代次数为4000.(更大的lr实测会发现loss爆炸为inf), 得到了53.7%的准确率,同时在测试集获得了52.4%的准确度. 而如果只迭代1000次,则准确率约为49%.

问题

调参的问题在上面已经回答过,这里就不再重复了

答案:1,2,3

原因: 间隙很大表明发生了过拟合, 也就是训练集表现很好, 测试集表现不如.  为此,1,2,3都有作用. 但值得注意的是, 在2中,增加隐含层元素个数和层数都有很明显的瓶颈效应,而且层数增加可能加剧过拟合. 讲义上的图可以明显说明这点:

1也不是随便乱加的, 需要很重视数据集的质量, 3的话, 虽然我们不能过拟合, 但是提升reg或许也会让测试集的效果下降, 所以我们应当合理控制过拟合的程度. 

讲义摘抄_激活函数

下面的内容仅仅是本人对官方讲义的一些摘抄和解说, 可能查重率会很高(

上面我们还有一点没做到,就是激活函数.我们用的ReLU是一个很常用的函数, 它梯度计算很简单, 而且容易收敛(相比于其他而言),但是一旦一个ReLu取0,则很有可能无法再次被激活, 此时相当于神经元死亡, 降低了可靠性. 按照讲义说法, 学习率合理设置能降低概率, 也就是我们不能随意增大学习率. leaky ReLUj解决了死亡问题, 也就是负向梯度很小而非为0. 但是这个目前效果没有一个统一的结论.

sigmoid是曾经很好的激活函数, 其输出可以正则化到(0,1), 但是其很容易发生梯度爆炸, 因为记f为sigmoid, f'(x)=f(x)(1-f(x)), 直接相乘很容易导致正向梯度消失, 反向梯度爆炸, 而且其输出不对称, 不过其影响没那么严重,tanh能解决这个问题.