大数定律

大数定律：

（1）切比雪夫大数定律：

　　随机变量X1，X2，X3........相互独立，数学期望 Ex 和 方差 Dx 都存在，并且方差有公共上界，则

　　　　算数平均值依概率收敛于数学期望

　　　　

 

 

（2）伯努利大数定律：

　　随机变量X1，X2，X3........服从参数为n和p的二项分布，即 Xn~B（n,p）,u是n重实验中A发生的次数，则

　　　　频率依概率收敛于统计概率

　　　　

 

 

（3）辛钦大数定律：

　　随机变量X1，X2，X3........相互独立且分布，期望存在，则

　　　　算数平均值依概率收敛于数学期望的确切解释

　　　　

 

 （4）独立同分布的中心极限定理：

　　　　前提条件：随机变量独立   同分布   数学期望与方差存在

　　　　当数据很多时，独立同分布随机变量的和近似服从正态分布

          

 

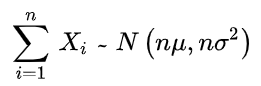
 （5）二项分布以正态分布为极限的中心极限定理：